模型简化与正则化：寻找过拟合与解释性的最佳平衡点

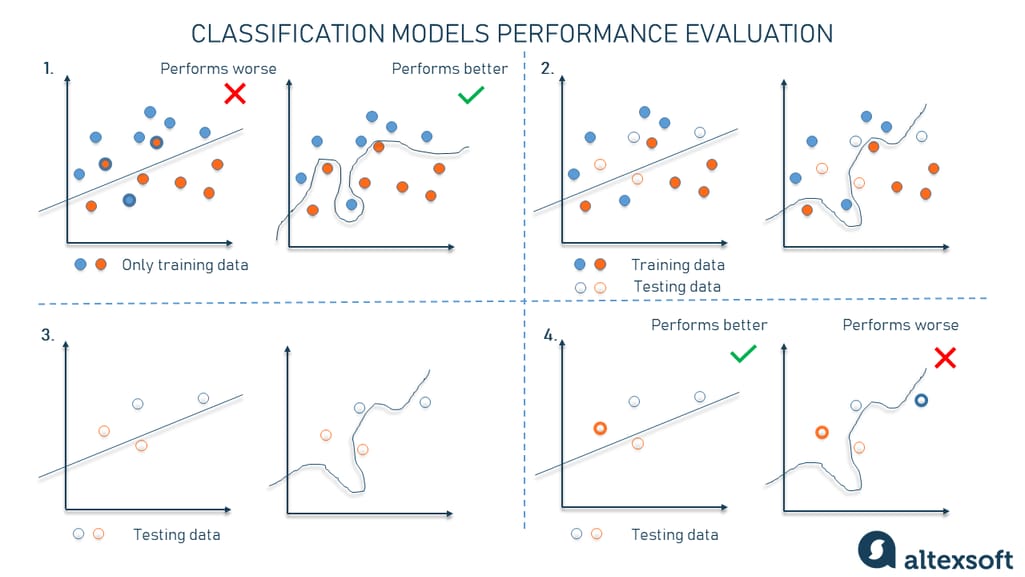
# 1. 过拟合与模型复杂度的基本概念

在机器学习和深度学习领域，一个模型在训练数据上表现出色，但在新数据上表现不佳的现象被称为过拟合。过拟合通常发生在模型过于复杂时，具体表现在模型试图记忆训练数据的所有细节，包括噪声和不重要的特征，而不是学习如何泛化到新的数据集。因此，模型复杂度成为影响模型性能的关键因素之一。

模型复杂度与模型的容量（capacity）密切相关，容量指的是模型能够学习数据的能力。如果模型的容量过高，它可能会捕捉到训练数据中的异常值和噪声，这就导致了过拟合。相反，如果模型容量不足，它可能无法捕捉到数据的真实结构，导致欠拟合。

因此，理解和处理模型复杂度，特别是在模型设计和训练过程中，是避免过拟合和提高泛化能力的关键步骤。本章将深入探讨过拟合与模型复杂度之间的关系，并为后续章节中探讨的模型简化技术打下理论基础。

# 2. 模型简化技术的理论基础

## 2.1 模型复杂度的影响因素

### 2.1.1 参数数量与模型容量

模型的参数数量直接影响模型的容量（capacity），即模型能够表达的复杂度。在统计学习中，模型容量通常指模型对于潜在函数的近似能力。参数越多，模型的容量就越高，理论上可以更好地拟合训练数据。然而，过高的模型容量可能使模型过度拟合，导致泛化能力下降。

以逻辑回归模型为例，一个二分类问题的逻辑回归模型通常有如下形式：

import numpy as np
from sklearn.linear_model import LogisticRegression

# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])

# 初始化逻辑回归模型
model = LogisticRegression(max_iter=1000)
model.fit(X, y)

在上述代码中，逻辑回归模型有两个参数（截距项和权重向量）。增加更多的特征或多项式特征会增加参数数量，提升模型的复杂度。

### 2.1.2 模型的表达能力与泛化误差

模型的表达能力是指模型描述数据特征的能力。一个模型的泛化误差是由偏差（Bias）和方差（Variance）构成的，偏差衡量的是模型的预测值与真实值之间的差距，方差衡量的是模型预测值的稳定性。

- 偏差高通常意味着模型欠拟合，模型过于简单无法捕捉数据的真实关系。
- 方差高则表示模型过拟合，模型复杂度太高而无法泛化到新的数据上。

下表简要说明了模型复杂度与偏差、方差之间的关系：

| 模型复杂度 | 偏差 | 方差 | 总误差 |
|------------|------|------|--------|
| 低 | 高 | 低 | 高 |
| 中等 | 中 | 中 | 中 |
| 高 | 低 | 高 | 中/高 |

一般来说，模型的复杂度与方差呈正相关，与偏差呈负相关。增加模型的复杂度会减少偏差，但同时可能会增加方差。因此，选择合适的模型复杂度以最小化总误差，是一个需要权衡的优化过程。

## 2.2 简化模型的方法论

### 2.2.1 特征选择与特征提取

特征选择是指从原始特征中选择一部分特征，以提高模型的泛化能力。特征提取是指通过某种映射转换原始数据到新的特征空间中，新的特征通常比原始特征少，有助于降低模型复杂度。

特征选择技术可以分为以下三类：

1. 过滤法（Filter methods）：使用统计测试（如卡方检验、ANOVA等）来评估特征和目标变量之间的相关性。
2. 包裹法（Wrapper methods）：使用学习算法反复训练模型，根据模型的性能来选择特征。
3. 嵌入法（Embedded methods）：在模型训练过程中实现特征选择，例如使用具有L1正则化的线性模型。

### 2.2.2 维度缩减技术简介

维度缩减技术旨在减少数据的特征空间维数，通过数据降维来简化模型。常用的技术有：

1. 主成分分析（PCA）：线性降维方法，通过正交变换将一组可能相关的变量转换为一组线性不相关的变量。
2. t分布随机邻域嵌入（t-SNE）：非线性降维方法，主要用于高维数据的可视化。
3. 自编码器（Autoencoders）：一种特殊的神经网络，用于学习数据的压缩表示。

以PCA为例，其基本步骤包括：

1. 标准化数据。
2. 计算协方差矩阵。
3. 提取特征值和特征向量。
4. 选择主成分。
5. 重构数据。

### 2.2.3 模型复杂度的数学度量

模型复杂度的数学度量包括多项式复杂度、VC维和参数数目等。例如：

- 多项式复杂度：模型的复杂度可以用模型参数的多项式次数来度量。
- VC维（Vapnik-Chervonenkis dimension）：衡量模型对数据集分类能力的一个指标，与模型复杂度成正比。

## 2.3 正则化技术的原理与应用

### 2.3.1 正则化的基本概念

正则化是一种避免模型过拟合的技术，通过在损失函数中引入惩罚项来控制模型复杂度。常见的正则化技术包括L1正则化、L2正则化等。

以线性回归模型为例，不带正则化的损失函数可以表示为：

from sklearn.linear_model import Ridge, Lasso

# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])

# Ridge回归（L2正则化）
ridge = Ridge(alpha=1.0)
ridge.fit(X, y)

在上述代码中，`alpha`是正则化强度参数，值越大，对权重的惩罚越强，模型越简单。

### 2.3.2 常见的正则化技术

- L1正则化（Lasso回归）：添加了权重绝对值的和的惩罚项，可以产生稀疏权重矩阵，有助于特征选择。
- L2正则化（Ridge回归）：添加了权重平方和的惩罚项，倾向于使权重均匀地较小，但不会完全为零。

### 2.3.3 正则化与模型简化的联系

正则化通过限制模型复杂度来简化模型，它在损失函数中增加了对权重大小的惩罚，从而减少了模型的方差。正则化技术的引入减少了模型对于训练数据的依赖，使得模型在未见数据上的表现更加稳定。

以L1正则化为例，其目标函数为：

# Lasso回归（L1正则化）
lasso = Lasso(alpha=1.0)
lasso.fit(X, y)

通过L1正则化，那些对模型贡献不大的特征的权重将趋于零，因而可以实现特征选择的效果。

在实际应用中，合理选择正则化方法和调整正则化参数是控制模型复杂度的关键。这通常需要通过交叉验证来确定最佳参数值，以达到最佳的模型简化效果。

# 3. 模型简化与正则化实践技巧

在第二章中，我们深入了解了模型简化技术的理论基础，包括模型复杂度的影响因素、简化模型的方法论以及正则化技术的原理与应用。在本章节中，我们将把理论与实践相结合，探讨如何在实际中运用这些技术以提升模型的性能。

## 3.1 正则化方法的实践应用

正则化是解决过拟合问题、提升模型泛化能力的重要手段。它通过在损失函数中添加一个额外的项，从而约束模型的复杂度，防止模型过于拟合训练数据。

### 3.1.1 L1与L2正则化在不同模型中的应用

L1正则化（Lasso回归）和L2正则化（Ridge回归）是最常见的两种正则化方法。

- **L1正则化**通过加入权重的绝对值之和作为惩罚项，能促使部分权重变为零，从而实现特征选择。它适用于特征选择，可以产生稀疏模型，有助于模型理解和特征