【MATLAB控制系统设计】：仿真到实现的全步骤教程

# 1. MATLAB控制系统设计概述

在现代控制系统设计中，MATLAB已经成为了工程师不可或缺的工具。它提供了一个综合性的计算环境，让工程师能够进行算法开发、数据可视化、数据分析以及仿真等多种操作。MATLAB的控制系统工具箱（Control System Toolbox）为控制系统的设计和分析提供了全面的支持。借助这些工具，我们可以轻松地对系统进行建模、分析和调整，以实现所需的动态性能。

控制系统设计不仅需要理解系统的理论基础，还需要掌握如何使用MATLAB进行实际操作。从控制系统的基本概念到仿真和优化，MATLAB都能够提供强大的支持，使得整个设计过程更加直观和高效。本章将介绍MATLAB在控制系统设计中的作用，并概述后文中将会详细介绍的理论基础和应用方法。

% 示例：创建一个简单的传递函数模型
num = [3 2 1]; % 分子多项式系数
den = [1 4 5]; % 分母多项式系数
sys = tf(num, den) % 创建传递函数模型

在上述代码中，我们使用MATLAB的tf函数创建了一个传递函数模型，该模型由分子多项式系数和分母多项式系数定义。这只是MATLAB在控制系统设计中所扮演角色的一个简单示例，接下来的章节将会深入探讨更多复杂和高级的应用。

# 2. 控制系统理论基础

## 2.1 控制系统的基本概念

### 2.1.1 控制系统定义与分类

控制系统是由若干个组成部分结合在一起，以实现对一个或多个变量进行调节或控制的系统。其核心目的是使得系统输出达到期望的性能指标，无论外界环境如何变化。控制系统广泛应用于工业生产、飞行器导航、日常生活等多个领域。

根据控制系统的工作原理和结构，控制系统大致可以分为以下几类：

- **按控制方式分类**：闭环控制系统、开环控制系统。
- **按系统的动态特性分类**：线性控制系统、非线性控制系统。
- **按系统的信号类型分类**：连续控制系统、离散控制系统。
- **按系统输出数量分类**：单输入单输出（SISO）系统、多输入多输出（MIMO）系统。

### 2.1.2 控制系统的工作原理

控制系统的工作原理基于负反馈机制，这是现代控制理论的核心概念之一。简而言之，控制系统通过测量输出变量并与期望值进行比较，计算出差值（误差信号），然后使用控制算法处理该误差信号，并通过控制元件对系统施加相应的调整作用，以减少误差，使系统输出稳定在期望状态。这一过程不断迭代，形成了一个闭环回路。

控制系统的工作流程可以用如下步骤简述：

1. **设定目标**：确立期望的系统输出目标或性能指标。
2. **测量输出**：实时检测系统的当前输出状态。
3. **误差计算**：与目标值对比，计算出误差信号。
4. **信号处理**：利用控制算法对误差信号进行处理，生成控制信号。
5. **执行动作**：控制信号作用于控制元件，对系统状态进行调整。
6. **反馈调整**：调整后的输出再次被测量，并与目标值进行比较，循环执行以上步骤。

## 2.2 数学建模与系统分析

### 2.2.1 线性系统模型

线性系统模型是描述控制系统中输入与输出关系的一种简化模型，它假设系统的输出与输入呈线性关系。在数学上，一个线性时不变（LTI）系统可以通过微分方程或差分方程来描述。

例如，连续时间系统的传递函数模型通常由拉普拉斯变换表示，形式如下：

\[ G(s) = \frac{Y(s)}{U(s)} = \frac{b_ms^m + b_{m-1}s^{m-1} + ... + b_1s + b_0}{s^n + a_{n-1}s^{n-1} + ... + a_1s + a_0} \]

其中，\(U(s)\)为系统输入的拉普拉斯变换，\(Y(s)\)为系统输出的拉普拉斯变换，\(a_i\)和\(b_i\)为系统参数。

线性系统的分析方法相对成熟，包括频域分析、根轨迹法等，这些方法在MATLAB中都提供了相应的工具箱函数进行辅助分析。

### 2.2.2 非线性系统模型

相对于线性系统，非线性系统更为复杂，因为非线性特性使得系统的输出不再是输入的线性函数。在实际工程中，许多系统都具有非线性特性，如饱和、死区、继电器特性等。

非线性系统模型不能用简单的线性方程来描述，而需要使用非线性微分方程或者差分方程。一个典型的非线性系统模型的例子是，考虑摩擦力的机械系统，摩擦力作为速度的非线性函数会影响系统的动态响应。

在分析非线性系统时，通常需要使用数值仿真或特殊的技术（如Poincaré映射、Lyapunov稳定性理论）来进行研究。MATLAB同样提供了强大的工具箱支持非线性系统的仿真和分析。

## 2.3 传递函数和状态空间表示

### 2.3.1 传递函数的推导和应用

传递函数是描述线性时不变系统动态特性的数学模型，它基于系统的输入-输出关系。传递函数的推导通常涉及对系统的微分方程进行拉普拉斯变换，消去时间变量，得到输入与输出之间的代数关系。

传递函数模型在控制系统设计中有着广泛的应用，它能够方便地进行系统性能分析，例如稳定性分析、时域和频域响应分析等。例如，考虑一个简单的一阶系统，其微分方程可以表示为：

\[ \tau\frac{dy}{dt} + y = Ku \]

其中，\(y\)是输出，\(u\)是输入，\(K\)是增益，\(\tau\)是时间常数。通过应用拉普拉斯变换，可以推导出其传递函数：

\[ G(s) = \frac{Y(s)}{U(s)} = \frac{K}{\tau s + 1} \]

在MATLAB中，可以使用以下代码块来推导该系统的传递函数，并且绘制其阶跃响应曲线：

% 定义系统参数
K = 1; % 系统增益
tau = 0.5; % 时间常数

% 创建传递函数模型
num = K; % 分子系数
den = [tau 1]; % 分母系数
sys = tf(num, den);

% 绘制阶跃响应曲线
figure;
step(sys);
title('阶跃响应');
grid on;

### 2.3.2 状态空间模型的构建和分析

状态空间模型为系统提供了一种多变量的描述形式，它用状态变量来描述系统的动态行为。状态空间模型由一组一阶微分方程和一组输出方程组成：

\[ \dot{x}(t) = Ax(t) + Bu(t) \]
\[ y(t) = Cx(t) + Du(t) \]

其中，\(x(t)\)是状态向量，\(u(t)\)是输入向量，\(y(t)\)是输出向量，\(A\)、\(B\)、\(C\)和\(D\)是系统矩阵，分别代表系统的动态特性、输入影响、输出组合和直接传递。

状态空间模型为控制系统的设计和分析提供了更丰富的信息，特别是对于多变量系统和复杂系统的分析。状态空间模型可以方便地进行系统稳定性分析、控制律设计等，并且特别适合使用MATLAB进行仿真和计算。

以下代码示例展示了如何在MATLAB中构建一个简单系统的状态空间模型，并进行仿真：

% 定义系统矩阵
A = [-2 -1; 1 0];
B = [1; 0];
C = [0 1];
D = 0;

% 创建状态空间模型
sys = ss(A, B, C, D);

% 仿真系统的阶跃响应
figure;
step(sys);
title('状态空间模型的阶跃响应');
grid on;

状态空间模型在MATLAB中的应用十分广泛，从系统设计到仿真验证，都是控制系统分析的重要工具。

# 3. MATLAB在控制系统仿真中的应用

## 3.1 MATLAB仿真环境搭建

MATLAB（Matrix Laboratory的缩写）是一个高性能的数值计算和可视化软件，广泛应用于工程计算、控制系统仿真等各个领域。为了进行控制系统仿真，首先要搭建好MATLAB的仿真环境。

### 3.1.1 MATLAB基础使用教程

在使用MATLAB进行仿真之前，用户需要熟悉MATLAB的基本操作。MATLAB的界面主要由命令窗口、工作空间、路径和搜索窗口等组成。其基础功能包括矩阵运算、绘图、编程、算法实现等。例如，一个简单的矩阵运算可以表示为：

A = [1, 2; 3, 4];
B = [5, 6; 7, 8];
C = A + B;  % 矩阵加法
disp(C);  % 显示结果

这段代码创建了两个矩阵`A`和`B`，执行了矩阵加法，然后使用`disp`函数显示了结果。

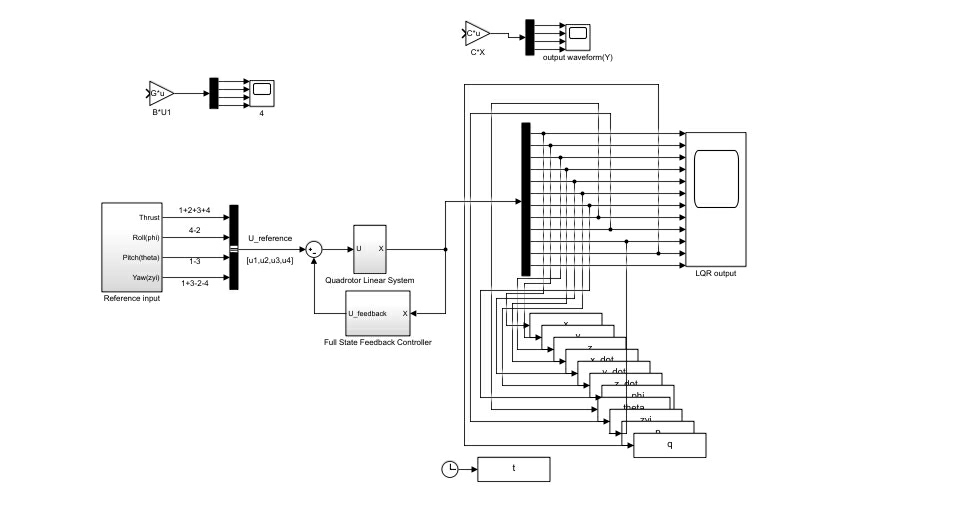
### 3.1.2 Simulink界面和功能介绍

Simulink是MATLAB的一个附加产品，它提供了一个可视化的仿真环境，使得用户可以通过拖放的方式构建复杂的系统仿真模型。Simulink支持多领域的动态系统，包括线性、非线性系统等。

用户可以通过在Simulink库中选择相应的功能块，例如信号源、增益、积分器、输出等，并将它们连接起来构成一个完整的仿真系统。如下图所示，这是一个典型的Simulink模型示例：

![Simulink模型示例](***

用户可以通过设置不同的参数来调整模型的特性，以达到期望的仿真效果。

## 3.2 控制系统仿真工具箱

MATLAB提供了丰富的工具箱，Control System Toolbox是其中专门用于控制系统设计与分析的工具箱，它包括了一系列方便用户设计和分析控制系统的函数和模块。

### 3.2.1 Control System Toolbox简介

Control System Toolbox为控制系统的设计和分析提供了全面的工具。它包括了建立和分析线性和非线性控制系统所需的所有功能。用户可以使用该工具箱来构建控制系统模型，执行系统分析，设计控制器，以及进行响应和稳定性分析等。

### 3.2.2 仿真工具箱中的关键函数和模块

仿真工具箱中包含了一些关键函数，如`tf`用于创建传递函数，`step`用于绘制单位阶跃响应，而`lsim`用于绘制线性系统的仿真响应。此外，Simulink中有专门用于控制系统的模块库，比如用于PID控制器设计的PID Controller模块，用于状态空间表示的State-Space模块等。下面是一个使用`step`函数绘制阶跃响应的示例代码：

s = tf('s');
G = 1/(s^2+3*s+2);  % 创建传递函数模型
step(G);            % 绘制阶跃响应

## 3.3 仿真模型的建立与分析

建立精确的仿真模型是进行控制系统仿真的核心，分析和验证仿真结果对于评估控制系统的性能至关重要。

### 3.3.1 建立数学模型

建立数学模型通常包括系统动力学