Python random模块与分布函数的邂逅：掌握随机数生成分布的奥秘

# 1. Python random模块概述**

Python random模块是一个内置模块，用于生成伪随机数。它提供了各种函数，可以生成不同分布的随机数，包括离散分布和连续分布。这些函数可以用于各种应用，如数据模拟、抽样、概率计算和统计分析。

random模块中的主要函数包括：

* **randint()：**生成指定范围内的随机整数。
* **randrange()：**生成指定范围内的随机整数，包括上限。
* **choice()：**从给定的序列中随机选择一个元素。
* **uniform()：**生成指定范围内的均匀分布随机数。
* **normal()：**生成正态分布随机数。
* **lognorm()：**生成对数正态分布随机数。

# 2. 随机数生成分布的理论基础

### 2.1 概率分布理论

概率分布理论是研究随机变量取值概率分布规律的一门数学学科。它在随机数生成、数据分析、统计建模等领域有着广泛的应用。

#### 2.1.1 离散分布

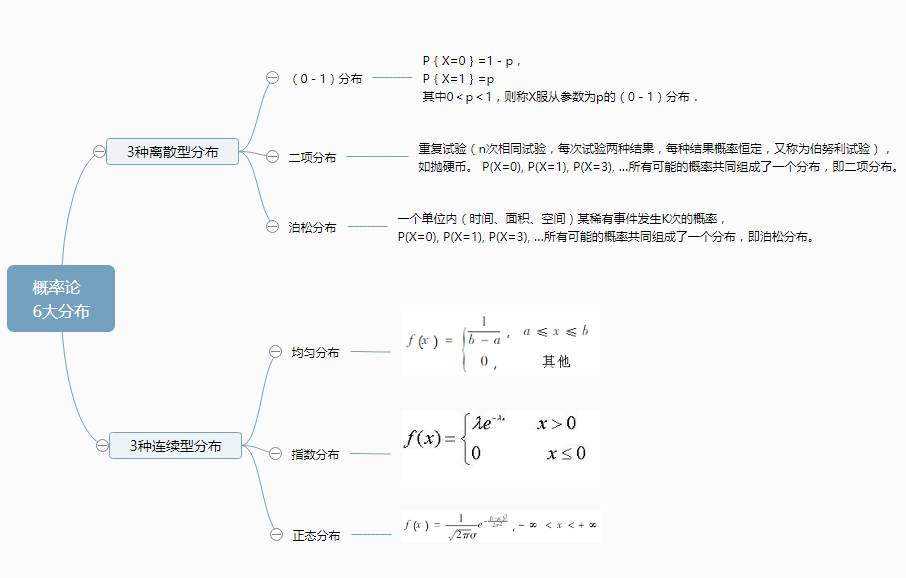
离散分布是指随机变量只能取有限个或可数无限个离散值的概率分布。常见的离散分布包括：

- **二项分布：**表示在 n 次独立试验中，成功 k 次的概率。
- **泊松分布：**表示在一段时间内发生 k 次事件的概率。
- **几何分布：**表示在 n 次独立试验中，第一次成功出现在第 k 次的概率。

#### 2.1.2 连续分布

连续分布是指随机变量可以取任何实数的概率分布。常见的连续分布包括：

- **均匀分布：**表示随机变量在某个区间内均匀分布的概率。
- **正态分布：**也称为高斯分布，表示随机变量呈钟形分布的概率。
- **指数分布：**表示随机变量表示事件发生的时间间隔的概率。

### 2.2 分布函数与概率密度函数

**分布函数**是随机变量取值小于或等于某个值的概率。对于离散分布，分布函数是一个阶梯函数；对于连续分布，分布函数是一个平滑的曲线。

**概率密度函数**是随机变量取某个值的概率。对于离散分布，概率密度函数是一个非负整数；对于连续分布，概率密度函数是一个非负函数。

分布函数和概率密度函数是描述随机变量分布的两种等价方式。分布函数可以通过概率密度函数积分得到，概率密度函数可以通过分布函数求导得到。

# 分布函数与概率密度函数之间的关系
import numpy as np

# 离散分布示例：二项分布
n = 10
k = 5
p = 0.5
binom_dist = np.random.binomial(n, p)

# 计算分布函数
dist_func = np.cumsum(binom_dist.pmf())
print("分布函数：", dist_func)

# 计算概率密度函数
prob_density = binom_dist.pmf()
print("概率密度函数：", prob_density)

# 3. random模块中的分布函数

### 3.1 离散分布函数

离散分布函数用于生成离散的随机数，即取值只能是有限个或可数无限个整数或小数的随机数。random模块中提供了三个离散分布函数：randint()、randrange()和choice()。

#### 3.1.1 randint()

randint()函数用于生成一个指定范围内的随机整数。其语法如下：

randint(a, b)

其中，a和b是整数，表示随机数的范围。randint()函数会生成一个[a, b]之间