【RC高通滤波器频域分析】：信号过滤的数学秘密


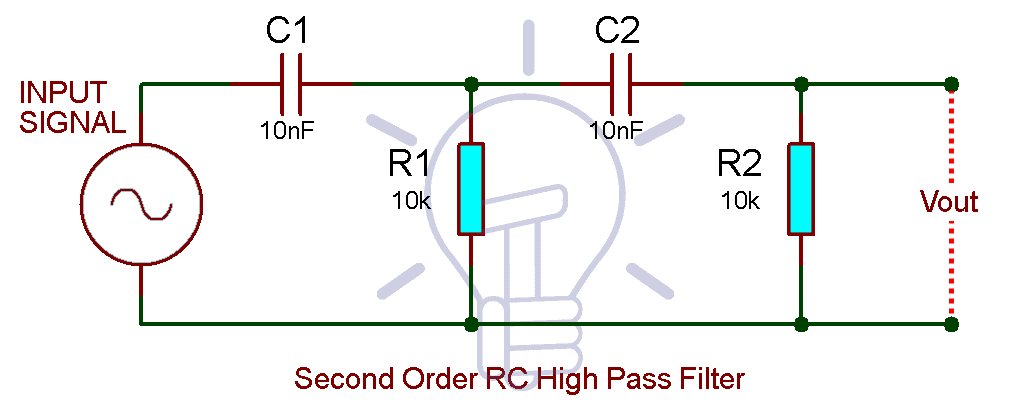
# 摘要
RC高通滤波器作为信号处理中的一种基础电路，广泛应用于各种电子系统中，用以滤除低频信号，保留或增强高频信号。本文首先概述了RC高通滤波器的原理与设计参数，随后详细分析了其频率响应特性，并通过实验设计验证了理论。文章还探讨了RC高通滤波器在不同应用中的实践案例，以及通过仿真与软件工具进行设计的高级技巧。通过对RC高通滤波器全面的理论分析和实践研究，本文旨在为工程技术人员提供深入的理解和高效的设计方法，以实现更精准的信号处理。

# 关键字
RC高通滤波器；信号处理；频率响应；设计参数；仿真软件；实验验证

参考资源链接：[RC高通滤波器的时域分析](https://wenku.csdn.net/doc/647c748bd12cbe7ec33d9fda?spm=1055.2635.3001.10343)
# 1. 信号处理中的RC高通滤波器概述

在信号处理领域，滤波器是不可或缺的组成部分，用于选择性地允许特定频率范围内的信号通过，并抑制其他频率的信号。RC高通滤波器是一种常见的电子电路，它只允许高于某一截止频率的信号成分通过，而阻止低频信号。该滤波器因结构简单、成本低廉而在众多应用中得到广泛使用，比如在音频处理、信号去噪、和通信系统中。

RC高通滤波器通常由一个电阻（R）和一个电容（C）组成。它的工作原理基于阻抗随频率变化的特性，电阻对所有频率信号的阻抗变化不大，而电容的阻抗则随频率升高而降低。因此，当输入信号频率高于设定的截止频率时，电容的阻抗会足够低，使得信号能够通过；低于截止频率时，电容的阻抗很高，信号会被阻止。

通过选择合适的电阻和电容值，可以定制高通滤波器的截止频率，以适应不同的应用场景。随着技术的演进，RC高通滤波器的设计与应用已经成为电子工程师和信号处理专家的重要工具之一。接下来的章节将会深入探讨RC高通滤波器的理论基础和实践应用。

# 2. RC高通滤波器的理论基础

## 2.1 信号滤波与频率响应

### 2.1.1 信号频域分析的基本概念

在信号处理中，频域分析是一种分析信号频率成分的方法，它将信号从时域转换到频域，利用傅里叶变换将时域信号分解为不同频率的正弦波和余弦波的叠加。这种方法使得我们能够识别信号中特定频率成分的存在与缺失，并对信号进行有效的滤波操作。在RC高通滤波器的应用场景中，频域分析用于理解信号在不同频率下的行为，并确定哪些频率成分需要被保留或被过滤掉。

频域分析中，我们通常会用到频率响应函数来描述一个系统对不同频率输入信号的反应。在RC高通滤波器的情况下，我们关注的是该滤波器在高频率下能够允许信号通过，而在低频率下阻断信号的特性。

### 2.1.2 高通滤波器的工作原理

高通滤波器（High-pass Filter, HPF）允许高于特定截止频率的信号通过，同时阻止低于该频率的信号。RC高通滤波器由一个电阻（R）和一个电容（C）构成，在电路中，它们共同决定了滤波器的截止频率。截止频率是滤波器开始显著减少信号幅度的频率点。

RC高通滤波器的工作原理可以通过电容器的充放电特性来理解。在低频时，电容器充电缓慢，因此它对电流的阻碍作用较大，导致输出信号减弱。随着频率的提高，电容器充电的时间常数相对减小，阻碍作用减弱，使得高频信号能够通过。这样，RC高通滤波器就实现了在高频率处的信号传递，而在低频率处的信号衰减。

## 2.2 RC高通滤波器的数学模型

### 2.2.1 RC电路的传递函数

RC高通滤波器的传递函数描述了输入信号和输出信号之间的数学关系。该传递函数通常表示为复频域变量s的函数，其中s = σ + jω，σ表示衰减因子，ω表示角频率。对于一个简单的RC高通滤波器，传递函数可以表达为：

H(s) = Vout(s) / Vin(s) = sRC / (1 + sRC)

其中，Vout(s)是滤波器输出端的电压，Vin(s)是输入端的电压。从这个传递函数，我们可以看出，当频率ω接近0（即低频）时，sRC的值较小，因此H(s)接近于0，意味着滤波器的输出电压很小，高通滤波器有效地阻断了低频信号。当频率ω增加时，sRC的值增大，H(s)趋近于1，使得高频信号可以被较好地传递。

### 2.2.2 频率响应函数的导出

RC高通滤波器的频率响应可以通过将传递函数中的s替换为jω来获得，即考虑角频率ω的影响。替换后得到的函数：

H(jω) = jωRC / (1 + jωRC)

为了分析频率响应，我们需要计算该函数的幅值和相位。幅值响应是输入和输出信号幅度的比值，可以表示为：

|H(jω)| = ωRC / sqrt(1 + (ωRC)^2)

相位响应则描述了输入信号与输出信号之间的相位差，表示为：

∠H(jω) = arctan(ωRC)

这些函数可以帮助我们进一步理解RC高通滤波器在不同频率下的表现，即幅频特性和相频特性。

## 2.3 高通滤波器的设计参数

### 2.3.1 截止频率的确定

截止频率（fc）是RC高通滤波器设计中的核心参数，它标志着滤波器开始显著降低信号幅度的频率点。RC高通滤波器的截止频率可以通过以下公式计算得出：

fc = 1 / (2πRC)

在设计过程中，需要根据应用需求来确定合适的截止频率，以确保滤波器能够有效地滤除不需要的低频成分，同时允许所需频率范围内的信号通过。

### 2.3.2 滤波器阶数的影响

RC高通滤波器的阶数指的是滤波器的复杂度，它影响了滤波器的斜率，即频率响应的变化率。一阶RC高通滤波器的斜率为-20dB/十倍频，这意味着每增加一个十倍频程，信号幅度衰减20dB。在实际应用中，如果需要更陡峭的频率衰减斜率，可能会采用多级RC高通滤波器，即二阶、三阶等。阶数越高，滤波器的频率响应斜率越陡峭，但同时相位失真和瞬态响应问题也更为复杂。因此，在设计RC高通滤波器时，需要平衡滤波效果和电路复杂度之间的关系。

# 3. RC高通滤波器的频率响应分析

## 3.1 频率域特性曲线
### 3.1.1 幅频特性曲线的解读
RC高通滤波器的幅频特性曲线显示了通过滤波器的信号幅度如何随输入信号频率的变化而变化。在理想情况下，频率低于截止频率的信号被大幅衰减，而频率高于截止频率的信号能够通过，且幅度保持在一个稳定的水平。

对于RC高通滤波器而言，幅频特性曲线通常表现为一个从低频到高频逐渐上升的曲线，这个上升的速度取决于RC时间常数。在截止频率处，曲线斜率发生变化，标志着频率的变化开始影响信号幅度。理想情况下，截止频率定义为信号幅度下降到其最大值的0.707倍（或下降-3dB）的频率点。

### 3.1.2 相频特性曲线的解读
相频特性曲线描述了滤波器对信号相位的影响，是频率的函数。对于RC高通滤波器，相位移动随着频率的增加而逐渐减小，这意味着高频信号比低频信号更接近于原信号的相位。

在截止频率附近，相位移动会发生剧烈变化，这可能在信号处理中引起问题，特别是当需要精确同步多个信号时。因此，