RC高通滤波器瞬态响应分析:信号处理的精确艺术
发布时间: 2025-01-02 18:42:50 阅读量: 8 订阅数: 11 


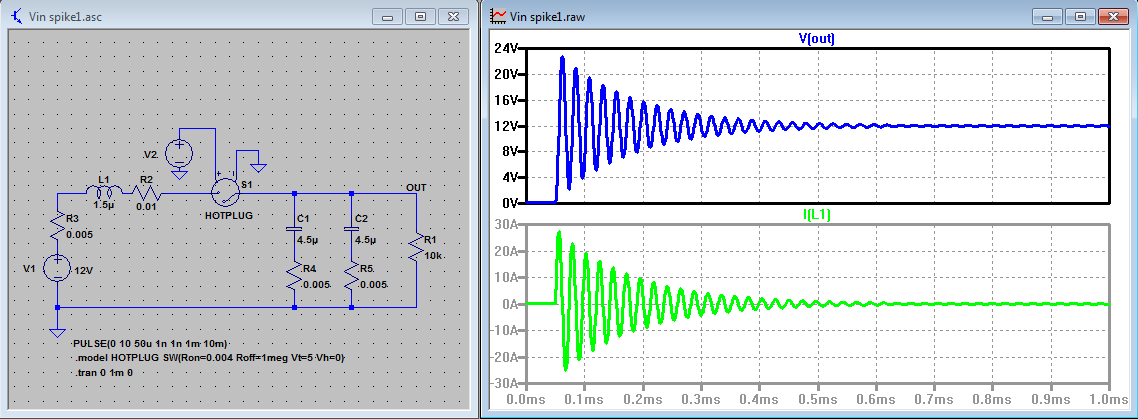
RC高通滤波器的时域分析
# 摘要
RC高通滤波器是电子电路设计中的基础组件,广泛应用于信号处理和电信领域。本文系统地介绍了RC高通滤波器的理论基础、设计实现、瞬态响应分析及其优化策略。首先阐述了RC高通滤波器的电路原理、传递函数和频率响应特性。然后详细描述了设计步骤,包括参数计算、电路仿真和元件选型,并进一步探讨了构建和测试过程中的标准方法。接着,本文深入分析了RC高通滤波器在输入阶跃和脉冲信号下的瞬态行为,并通过数学建模探索了瞬态响应。此外,本文还提出了一系列针对瞬态响应的优化策略,并通过实践案例分析验证了滤波器在实际应用中的效能。最后,探讨了多阶RC高通滤波器的设计以及与其他类型滤波器的比较,展望了RC高通滤波器的未来发展趋势。本文旨在为工程师和研究人员提供RC高通滤波器设计和应用的全面指南。
# 关键字
RC高通滤波器;电路原理;瞬态响应;设计优化;数学建模;信号处理
参考资源链接:[RC高通滤波器的时域分析](https://wenku.csdn.net/doc/647c748bd12cbe7ec33d9fda?spm=1055.2635.3001.10343)
# 1. RC高通滤波器的理论基础
## 1.1 RC高通滤波器的定义和功能
RC高通滤波器是一种电子电路,其主要功能是允许高于特定截止频率的交流信号通过,同时阻止低于该频率的信号。这种滤波器是由一个电阻(R)和一个电容(C)组成的简单电路,其核心作用是实现频率选择性。
## 1.2 RC高通滤波器的工作原理
RC高通滤波器的工作原理基于电容器对交流信号的阻抗特性。频率越高,电容器的阻抗越小,信号越容易通过;反之,频率越低,电容器的阻抗越大,信号越难通过。电阻和电容的组合形成了一个具有特定截止频率的滤波器。
## 1.3 RC高通滤波器的数学模型
RC高通滤波器的数学模型通常表示为一个传递函数,该函数描述了输入信号和输出信号之间的关系。传递函数涉及到频率变量,其表达形式与电路中电阻和电容的值有关。理解该数学模型对于设计和分析RC高通滤波器至关重要。
# 2. RC高通滤波器的设计与实现
## 2.1 RC高通滤波器的电路原理
### 2.1.1 电阻和电容的基本特性
电阻(R)和电容(C)是构建RC高通滤波器(HPF)的基本元件。电阻的阻值(Ohm)决定电路中电流的流动难度,而电容的容值(Farad)决定其存储电荷的能力。在高通滤波器设计中,电阻通常被视为一个不变的电阻器,而电容器则根据频率的不同来允许或阻止交流信号的流动。
电阻器的电流与电压之间的关系由欧姆定律(V=IR)给出,而电容器具有一个与电压变化率成正比的电流特性。这些基本特性的数学表达式对于理解RC高通滤波器的工作原理至关重要。
```math
I_R = \frac{V}{R} \quad \text{(欧姆定律)}
```
```math
I_C = C \frac{dV}{dt} \quad \text{(电容器的电流特性)}
```
### 2.1.2 RC电路的传递函数和频率响应
RC电路的传递函数是其输出与输入之间关系的数学表示。对于RC高通滤波器,传递函数将决定哪些频率的信号被允许通过。传递函数通常以频率变量(如s域中的s或f域中的jω)表示。
传递函数在s域中可以表示为:
```math
H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{R}{R + \frac{1}{sC}}
```
其中,`V_{out}(s)`是输出信号,`V_{in}(s)`是输入信号,R是电阻值,C是电容值,s是复频率域变量。
频率响应是传递函数对信号频率的响应,通常以幅度和相位来描述。在高通滤波器中,幅度响应表明了频率高于截止频率的信号将被允许通过,而低于截止频率的信号将被衰减。
```math
|H(jω)| = \frac{1}{\sqrt{1 + (ωRC)^2}}
```
```math
∠H(jω) = -\arctan(ωRC)
```
## 2.2 RC高通滤波器的设计步骤
### 2.2.1 滤波器参数的计算方法
设计RC高通滤波器的第一步是确定滤波器的截止频率(f_c),这是区分信号频率被允许通过或衰减的边界频率。计算方法如下:
```math
f_c = \frac{1}{2πRC}
```
其中,`f_c`是截止频率,`R`是电阻值(单位:欧姆),`C`是电容值(单位:法拉)。
### 2.2.2 滤波器的电路仿真和元件选型
设计阶段的下一步是通过电路仿真软件(例如SPICE)进行测试。通过仿真,设计者可以验证理论计算的截止频率,还可以观察到不同频率信号的实际响应。根据仿真结果,可能需要对元件值进行微调以获得最佳性能。
选择合适的电阻和电容器件是实现设计目标的关键。在选择元件时,要考虑额定功率、温度系数、耐压值、公差等因素,以确保滤波器在不同条件下都能稳定工作。
## 2.3 RC高通滤波器的构建与测试
### 2.3.1 搭建RC高通滤波器的实验步骤
在完成理论计算和仿真测试后,下一步是物理搭建RC高通滤波器。搭建步骤如下:
1. 准备所需的电阻和电容元件。
2. 按照电路原理图连接元件,使用面包板或印刷电路板(PCB)。
3. 使用万用表确认连接正确且无短路或开路。
### 2.3.2 测量和验证滤波器性能的标准方法
一旦RC高通滤波器被搭建起来,接下来需要测量和验证其性能,确保它符合设计规格。以下是标准的测试步骤:
1. 使用信号发生器产生一系列不同频率的正弦波信号作为输入信号。
2. 使用示波器或频谱分析仪观察输出信号,记录幅度和相位的响应。
3. 通过调整信号发生器的频率,确定截止频率并记录其幅度下降3dB点的确切位置。
4. 检查频率响应曲线是否符合设计预期,特别是截止频率附近的过渡带宽。
完成以上步骤后,RC高通滤波器的构建与测试部分即告完成,可以进行实际应用或者进一步的优化和调整。
# 3. RC高通滤波器的瞬态响应分析
RC高通滤波器是电子信号处理中不可或缺的
0
0





