反双曲正弦函数：在机器学习和数据分析中的必备指南

# 1. 反双曲正弦函数的数学基础

反双曲正弦函数（sinh^-1）是双曲正弦函数（sinh）的反函数，它将双曲正弦值映射回其对应的自变量。其定义如下：

sinh^-1(x) = ln(x + sqrt(x^2 + 1))

其中，x 是双曲正弦函数的输入值。

反双曲正弦函数具有以下数学性质：

- **单调性：**sinh^-1(x) 是一个单调递增函数，其值域为 [-∞, ∞]。
- **奇偶性：**sinh^-1(-x) = -sinh^-1(x)，即反双曲正弦函数是奇函数。
- **导数：**d/dx sinh^-1(x) = 1 / sqrt(x^2 + 1)。

# 2. 反双曲正弦函数在机器学习中的应用

反双曲正弦函数（asinh）在机器学习领域有着广泛的应用，特别是在逻辑回归和神经网络中。

### 2.1 逻辑回归

#### 2.1.1 逻辑回归模型

逻辑回归是一种二分类模型，用于预测一个二元事件发生的概率。其模型方程为：

p = 1 / (1 + exp(-(b + w1 * x1 + w2 * x2 + ...)))

其中：

* `p` 是事件发生的概率
* `b` 是偏置项
* `w1`, `w2`, ... 是特征权重
* `x1`, `x2`, ... 是特征值

#### 2.1.2 反双曲正弦函数在逻辑回归中的作用

在逻辑回归中，反双曲正弦函数可以作为激活函数，将输入的线性组合转换为概率值。其公式为：

p = asinh(b + w1 * x1 + w2 * x2 + ...)

反双曲正弦函数具有以下优点：

* 单调递增，保证输出概率在 0 到 1 之间
* 非线性，可以捕捉数据中的复杂关系
* 平滑，避免梯度消失或爆炸问题

### 2.2 神经网络

#### 2.2.1 神经网络结构

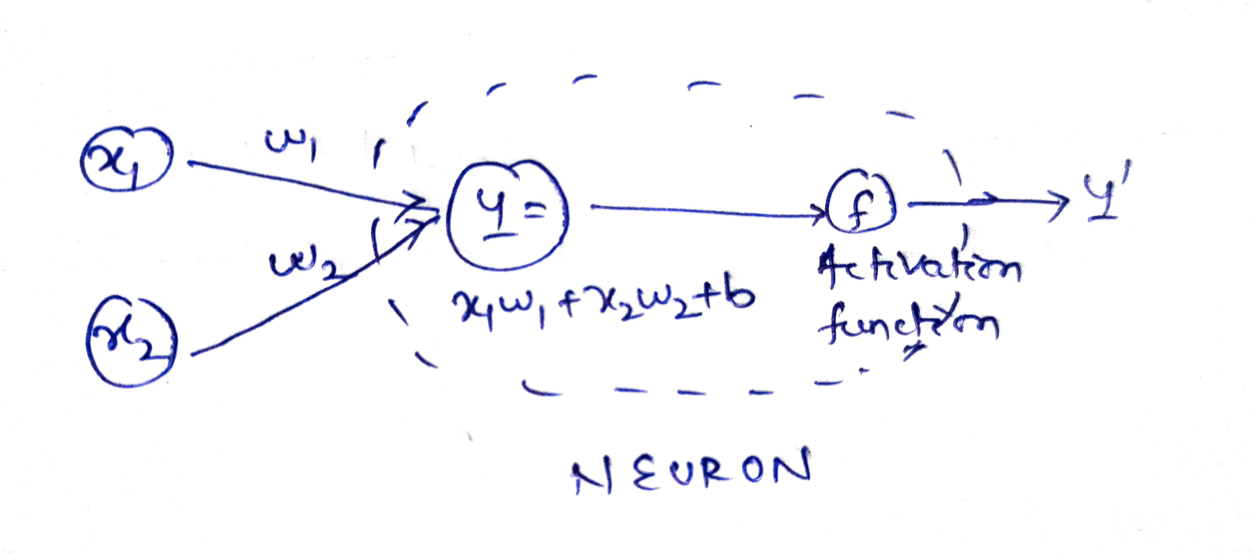
神经网络是一种多层感知器，由输入层、隐藏层和输出层组成。每一层由多个神经元组成，神经元之间通过权重连接。

#### 2.2.2 反双曲正弦函数在神经网络中的应用

在神经网络中，反双曲正弦函数可以作为隐藏层或输出层的激活函数。其作用是将神经元的输入信号转换为输出信号。

反双曲正弦函数在神经网络中的优点包括：

* 非线性，可以学习复杂的数据模式
* 平滑，避免梯度消失或爆炸问题
* 适用于各种任务，如分类、回归和生成式建模

**代码示例：**

import numpy as np

# 定义神经网络
class NeuralNetwork:
    def __init__(self, layers):
        self.layers = layers

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

# 定义反双曲正弦激活函数
class AsinhActivation:
    def forward(self, x):
        return np.asinh(x)

# 创建神经网络
network = NeuralNetwork([
    LinearLayer(10),
    AsinhActivation(),
    LinearLayer(1)
])

# 训练神经网络

# 使用神经网络进行预测
y_pred = network.forward(x)

**逻辑分析：**

* `LinearLayer` 是一个线性层，用于计算输入和权重的线性组合。
* `AsinhActivation` 是反双曲正弦激活函数，将线性组合转换为非线性输出。
* `forward` 方法是神经网络的前向传播过程，依次计算每一层的输出。
* `y_pred` 是神经网络的预测输出。

# 3. 反双曲正弦函数在数据分析中的应用

反双曲正弦函数在数据分析中具有广泛的应用，主要体现在数据归一化和数据可视化两个方面。

### 3.1 数据归一化

#### 3.1.1 数据归一化的必要性

数据归一化是一种将数据映射到特定范围（通常为 [0, 1] 或 [-1, 1]）的技术。它可以消除不同特征之间量纲和范围的差异，从而提高模型的性能和可解释性。

#### 3.1.2 反双曲正弦函数在数据归一化中的作用

反双曲正弦函数是一种非线性变换，它可以将任意范围的数据映射到 [-1, 1] 范围内。其表达式为：

asinh(x) = ln(x + sqrt(x^2 + 1))

反双曲正弦函数具有以下优点：

- **保持数据分布：**它保留了原始数据的分布形状，避免了线性归一化方法可能导致的数据失真。
- **处理异常值：**它可以有效地处理异常值，将其映射到接近 -1 或 1 的极值，从而减轻其对模型的影响。

### 3.2 数据可视化

#### 3.2.1 数据可视化的重要性

数据可视化是将数据以图形或图表的形式呈现，以便于理解和分析。它可以帮助发现数据中的模式、趋势和异常值。

#### 3.2.2 反双曲正弦函数在数据可视化中的应用

反双曲正弦函数可以用于创建具有以下优点的非线性数据可视化：

- **放大细节：**它可以放大数据中的细微变化，使其更易于识别。
- **处理异常值：**它可以将异常值映射到极值，使其在可视化中更加突出。
- **改善可读性：**它可以使数据分布更加均匀，从而提高可读性和可解释性。

**示例：**

下图展示了反双曲正弦函数在数据可视化中的应用。左侧为原始数据分布，右侧为使用反双曲正弦函数转换后的数据分布。可以看到，转换后的分布更加均匀，异常值更加突出。

# 4. 反双曲正弦函数的实现与优化

### 4.1 反双曲正弦函数的数值计算方法

#### 4.1.1 泰勒级数展开

泰勒级数展开是一种将函数表示为无限级数的方法。对于反双曲正弦函数，其泰勒级数展开式为：

sinh^{-1}(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...

其中，x 为输入值。

**参数说明：**

* x：输入值

**代码逻辑：**

def sinh_inv_taylor(x, n):
    """
    使用泰勒级数展开计算反双曲正弦函数。

    参数：
        x：输入值
        n：展开项数

    返回：
        反双曲正弦函数值
    """
    result = 0
    for i in range(1, n + 1):
        result += (-1)**(i - 1) * x**(2 * i - 1) / math.factorial(2 * i - 1)
    return result

#### 4.1.2 分段线性逼近

分段线性逼近是一种将函数近似为一系列线性段的方法。对于反双曲正弦函数，可以将其分为多个线性段，并使用线性函数近似每个线性段。

**参数说明：**

* x：输入值
* x_values：线性段的端点值
* y_values：线性段的函数值

**代码逻辑：**

def sinh_inv_linear(x, x_values, y_values):
    """
    使用分段线性逼近计算反双曲正弦函数。

    参数：
        x：输入值
        x_values：线性段的端点值
        y_values：线性段的函数值

    返回：
        反双曲正弦函数值
    """
    for i in range(len(x_values) - 1):
        if x >= x_values[i] and x < x_values[i + 1]:
            slope = (y_values[i + 1] - y_values[i]) / (x_values[i + 1] - x_values[i])
            y_intercept = y_values[i] - slope * x_values[i]
            return slope * x + y_intercept
    raise ValueError("输入值超出线性段范围")

### 4.2 反双曲正弦函数的优化技巧

#### 4.2.1 精度控制

在计算反双曲正弦函数时，精度控制非常重要。可以通过设置泰勒级数展开的项数或分段线性逼近的线性段数量来控制精度。

#### 4.2.2 速度优化

对于需要高性能计算的应用，可以采用以下优化技巧：

* 使用预计算表：预先计算反双曲正弦函数值并存储在表中，以避免重复计算。
* 使用近似算法：使用近似算法，如分段线性逼近，可以牺牲一些精度以换取更高的速度。
* 并行计算：将计算任务并行化到多个处理器或 GPU 上。

# 5. 反双曲正弦函数的应用案例

反双曲正弦函数在实际应用中有着广泛的应用场景，以下列举两个典型的应用案例：

### 5.1 欺诈检测

**5.1.1 欺诈检测的挑战**

欺诈检测旨在识别和防止欺诈性交易，是一项具有挑战性的任务。欺诈者往往采用复杂的手段来伪装其行为，使得传统检测方法难以奏效。

**5.1.2 反双曲正弦函数在欺诈检测中的应用**

反双曲正弦函数在欺诈检测中发挥着重要作用。它可以将交易数据映射到一个非线性空间中，从而放大欺诈性交易与正常交易之间的差异。具体来说，反双曲正弦函数可以用于：

- **特征工程：**将原始交易数据（如交易金额、时间、地点等）转换为非线性特征，增强欺诈检测模型的区分能力。
- **模型训练：**使用反双曲正弦函数转换后的特征训练欺诈检测模型，提高模型的准确性和鲁棒性。

### 5.2 推荐系统

**5.2.1 推荐系统的原理**

推荐系统旨在为用户提供个性化的内容或产品推荐，是电子商务和社交媒体等领域的重要应用。推荐系统通常基于协同过滤或内容过滤等技术，通过分析用户行为和物品属性来生成推荐。

**5.2.2 反双曲正弦函数在推荐系统中的应用**

反双曲正弦函数在推荐系统中可以用于：

- **相似度计算：**将用户或物品之间的相似度映射到一个非线性空间中，增强相似度计算的精度和鲁棒性。
- **推荐生成：**使用反双曲正弦函数转换后的相似度生成推荐列表，提高推荐结果的多样性和相关性。