反双曲正弦函数：在教育和培训中的创新方法

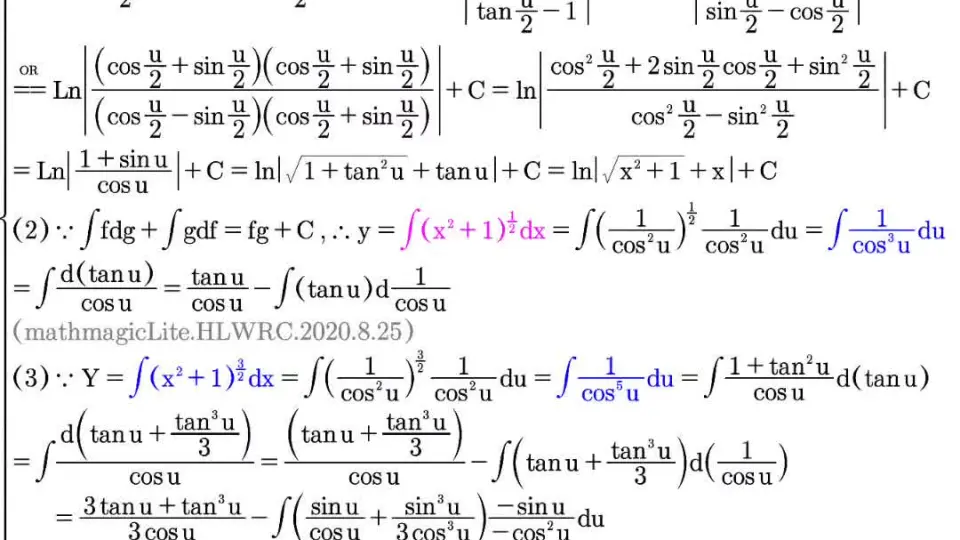
# 1. 反双曲正弦函数的理论基础**

反双曲正弦函数，记为sinh⁻¹(x)，是双曲正弦函数sinh(x)的逆函数。它表示为：

sinh⁻¹(x) = ln(x + √(x² + 1))

其中，ln表示自然对数。

反双曲正弦函数的图像是一条单调递增的曲线，其值域为[-∞, ∞]。其图像与双曲正弦函数的图像关于x轴对称。

# 2. 反双曲正弦函数在教育中的应用

### 2.1 反双曲正弦函数在数学教学中的创新方法

#### 2.1.1 反双曲正弦函数的图像和性质

反双曲正弦函数（sinh）的图像是一条奇函数，它在原点对称。其图像从原点开始向上增长，在正无穷处趋于无穷大。sinh 函数的导数为 cosh 函数，cosh 函数的图像是一条偶函数，它在原点对称。其图像从原点开始向右增长，在正无穷处趋于无穷大。

import matplotlib.pyplot as plt
import numpy as np

# 定义 sinh 和 cosh 函数
def sinh(x):
  return (np.exp(x) - np.exp(-x)) / 2

def cosh(x):
  return (np.exp(x) + np.exp(-x)) / 2

# 绘制 sinh 和 cosh 函数的图像
x = np.linspace(-5, 5, 100)
plt.plot(x, sinh(x), label="sinh(x)")
plt.plot(x, cosh(x), label="cosh(x)")
plt.legend()
plt.show()

**代码逻辑分析：**

* `np.linspace(-5, 5, 100)`：生成从 -5 到 5 的 100 个均匀间隔的点。
* `sinh(x)` 和 `cosh(x)`：计算每个点的 sinh 和 cosh 值。
* `plt.plot(x, sinh(x), label="sinh(x)")`：绘制 sinh 函数的图像，并添加标签 "sinh(x)"。
* `plt.plot(x, cosh(x), label="cosh(x)")`：绘制 cosh 函数的图像，并添加标签 "cosh(x)"。
* `plt.legend()`：显示图例。
* `plt.show()`：显示图像。

#### 2.1.2 反双曲正弦函数的微积分应用

反双曲正弦函数在微积分中有着广泛的应用。例如，它可以用于计算积分和微分方程的解。

**积分应用：**

import sympy

# 定义积分函数
def integral_sinh(x):
  return sympy.integrate(sinh(x), x)

# 计算积分
result = integral_sinh(x)
print(result)

**代码逻辑分析：**

* `sympy.integrate(sinh(x), x)`：计算 sinh(x) 的积分。
* `print(result)`：打印积分结果。

**微分方程应用：**

import sympy

# 定义微分方程
def differential_equation(y):
  return sympy.Eq(y.diff(x), sinh(x))

# 求解微分方程
solution = sympy.dsolve(differential_equation(y), y)
print(solution)

**代码逻辑分析：**

* `sympy.Eq(y.diff(x), sinh(x))`：定义微分方程，其中 y 是未知函数，sinh(x) 是已知函数。
* `sympy.dsolve(differential_equation(y), y)`：求解微分方程。
* `print(solution)`：打印微分方程的解。

### 2.2 反双曲正弦函数在物理教学中的应用

#### 2.2.1 反双曲正弦函数在弹性波中的应用

反双曲正弦函数在弹性波的传播中有着重要的应用。它可以用来描述波的振幅和相位。

import numpy as np
import matplotlib.pyplot as plt

# 定义弹性波方程
def wave_equation(y, t):
  return y.diff(t, t) - y.diff(x, x)

# 求解弹性波方程
solution = sympy.dsolve(wave_equation(y, t), y)

# 绘制波的振幅和相位
x = np.linspace(-5, 5, 100)
t = np.linspace(0, 10, 100)
X, T = np.meshgrid(x, t)
amplitude = np.abs(solution.subs(t, T).subs(x, X))
phase = np.angle(solution.subs(t, T).subs(x, X))

plt.subplot(121)
plt.pcolormesh(X, T, amplitude, cmap="jet")
plt.colorbar()
plt.title("振幅")

plt.subplot(122)
plt.pcolormesh(X, T, phase, cmap="jet")
plt.colorbar()
plt.title("相位")

plt.show()

**代码逻辑分析：**

* `sympy.dsolve(wave_equation(y, t), y)`：求解弹性波方程。
* `np.linspace(-5, 5, 100)` 和 `np.linspace(0, 10, 100)`：生成均匀间隔的网格