【扩散模型中的正定性问题研究】： 研究扩散模型中的正定性问题

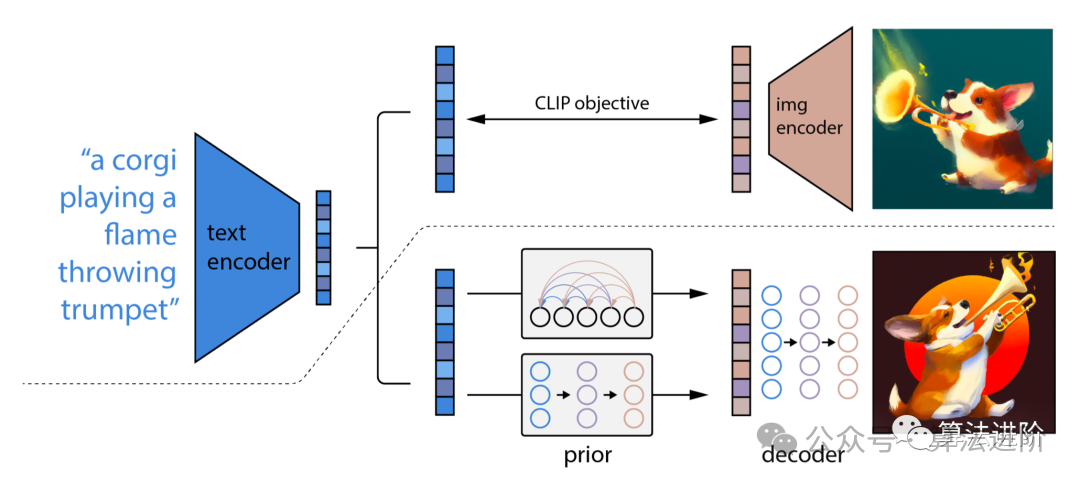
# 1. 理论基础

在深入探讨扩散模型的概念和具体应用之前，我们首先需要建立起相关的理论基础。理解扩散模型所涉及的数学描述、模型分类以及初始条件和边界条件的重要性是非常关键的。通过本章的学习，读者将能够全面理解扩散模型领域的基本概念，为后续章节的内容打下坚实的基础。

# 2. 扩散模型概述

### 2.1 什么是扩散模型
扩散模型是一种数学模型，用于描述某一现象或变量在空间和时间上的传播过程。在实际应用中，扩散模型被广泛应用于生态学、经济学、医学等领域。

#### 2.1.1 定义和应用领域
扩散模型是通过数学方程来模拟和预测物质或信息在空间上的传播与扩散规律。它在环境科学中用于分析污染物传播、在生态学中用于研究物种分布变化，同时在社会网络和市场营销中也有重要应用。

#### 2.1.2 扩散模型的分类
扩散模型根据不同的研究对象和条件可以分为线性扩散模型和非线性扩散模型两大类。线性扩散模型利用线性微分方程描述传播过程，非线性扩散模型则包括更为复杂的微分方程模型。

### 2.2 扩散模型的数学描述

#### 2.2.1 方程形式
扩散模型的数学描述通常采用偏微分方程来表示，其中包括时间变量和空间变量。常见的扩散过程会用到扩散系数、源项等参数。

#### 2.2.2 变量说明
- $u(x, t)$：表示在时刻 $t$ 和空间点 $x$ 处的扩散物质浓度或状态变量。
- $D$：扩散系数，描述物质在空间上的传播速率。
- $f(u)$：源项函数，描述外部因素对物质扩散的影响。

#### 2.2.3 初始条件和边界条件
扩散模型通常需要给出初始条件和边界条件，如初始时刻的浓度分布，空间边界处的浓度等。这些条件对于求解扩散模型的数值解非常关键。

这是扩散模型概述的部分内容，接下来将深入探讨扩散模型的正定性问题分析。

# 3. 正定性问题分析

### 3.1 正定性概念解析
在扩散模型中，正定性是一个重要的问题，下面将对正定性进行详细解析。

#### 3.1.1 正定性定义
正定性是指在扩散模型中，解的某些性质能够被确保为非负。简而言之，即解的稳定性和非负性。正定性定义的具体表述可以根据问题领域的不同而有所区别。

#### 3.1.2 正定性在扩散模型中的重要性
在扩散模型中，正定性是确保数值解的准确性和稳定性的重要条件。如果扩散模型不满足正定性条件，可能会导致数值解的不稳定性，甚至产生负数解，严重影响模型的准确性和可靠性。

### 3.2 正定性条件
正定性条件是保证扩散模型解的非负性和稳定性的关键条件，下面将具体解析正定性的相关条件。

#### 3.2.1 Laplace算子
在扩散模型中，Laplace算子是描述空间中扩散量变化的关键算子。其在数学描述中是一个二阶椭圆型偏微分方程算子，在保证解的正定性方面发挥着重要作用。

#### 3.2.2 矩阵正定性判定方法
除了Laplace算子外，正定性的判定还可以通过矩阵正定性来进行。通过对扩散模型的离散化形式进行矩阵化，进而判断矩阵是否正定，从而保证解的稳