贝叶斯方法：过拟合预防的理论基础与应用案例分析

# 1. 贝叶斯方法概述

在当今的数据密集型和模型驱动型世界中，贝叶斯方法提供了一种强有力的统计推理工具，特别是在不确定性量化和决策制定方面。这种统计推断框架在处理不完整、不确定或模糊数据时显示出其独特的优势。贝叶斯方法的核心在于其能够融合先验知识和实际观察结果，从而得到后验概率分布，这种动态更新的能力使贝叶斯方法在众多应用领域变得极为重要，从基础科学研究到实际的商业决策中都发挥着巨大作用。在后续章节中，我们将深入探讨贝叶斯定理、推断过程以及在实际应用中如何预防过拟合，并分析其在高级主题如非参数贝叶斯模型和贝叶斯深度学习中的应用。

# 2. 理论基础：贝叶斯推断

## 2.1 贝叶斯定理

### 2.1.1 条件概率与贝叶斯定理

贝叶斯定理是概率论中的一个定理，它提供了一种在已知其他相关事件概率的条件下，计算一个事件概率的方法。该定理基于条件概率的概念，条件概率指的是在已知一个或多个事件已经发生的条件下，另一事件发生的概率。

贝叶斯定理的公式形式如下：

\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]

其中：
- \( P(A|B) \) 表示在事件B发生的条件下，事件A发生的条件概率。
- \( P(B|A) \) 表示在事件A发生的条件下，事件B发生的条件概率。
- \( P(A) \) 和 \( P(B) \) 分别是事件A和B的边缘概率。

这个公式的美妙之处在于，它允许我们在已知其他事件发生的情况下，更新对特定事件发生的信念。

### 2.1.2 贝叶斯定理的概率解释

贝叶斯定理的一个关键应用是在统计推断中，尤其是在贝叶斯推断方法中。在贝叶斯推断中，我们可以用贝叶斯定理来计算后验概率。后验概率是在考虑了观测数据后，对未知参数的最新估计。

后验概率 \( P(\theta|X) \) 可以通过贝叶斯定理计算得出，其中 \( \theta \) 是我们要估计的参数，\( X \) 是观测到的数据。

\[ P(\theta|X) = \frac{P(X|\theta) \cdot P(\theta)}{P(X)} \]

这里的 \( P(X|\theta) \) 称为似然函数（likelihood），\( P(\theta) \) 是先验概率（prior probability），它代表了在观测数据之前对参数的信念，而 \( P(X) \) 称为边缘似然函数（marginal likelihood），它确保后验概率是规范的。

通过这种方式，贝叶斯定理提供了一种在已知数据和先验知识的条件下，如何更新我们对模型参数信念的明确框架。

## 2.2 先验与后验分布

### 2.2.1 先验分布的选择

在应用贝叶斯推断时，先验分布的选择是一个重要的步骤，因为它直接影响到后验分布的形状和最终的推断结果。先验分布可以是基于领域知识、历史数据或者其他信息的主观选择，也可以是无信息先验，其设计为对参数几乎没有任何影响，从而让数据本身占据主导地位。

先验的类型通常分为以下几种：
- 共轭先验（Conjugate Prior）：选择与似然函数形式相同的先验分布，简化后验分布的计算。
- 非信息先验（Non-informative Prior）：尽量不引入主观信息，让数据说话。
- 弱信息先验（Weakly Informative Prior）：比非信息先验稍微提供一些信息，但不足以影响结果。
- 信息先验（Informative Prior）：基于领域专家知识或者先前的研究，对模型参数有着明确的信念。

选择先验时，需要根据问题的性质和可用信息来进行，必要时可以通过敏感性分析来评估不同先验选择对结果的影响。

### 2.2.2 后验分布的计算

计算后验分布是贝叶斯推断的核心内容。在已知似然函数和先验分布的情况下，后验分布可以通过贝叶斯定理获得。后验分布代表了考虑了所有先验信息和新观测数据之后，对参数的最新概率评估。

以贝叶斯定理为基础，后验分布可以写作：

\[ P(\theta|X) = \frac{P(X|\theta) \cdot P(\theta)}{\int P(X|\theta') \cdot P(\theta') d\theta'} \]

这里，分母是边缘似然函数，它是所有可能参数值下的似然函数乘以先验概率的积分。这个积分对于复杂模型来说可能计算困难，这就是为什么共轭先验在实际应用中特别受欢迎的原因，因为它们可以简化积分计算。

然而，在实际操作中，直接计算这个积分是不可行的，特别是对于高维参数空间。因此，在计算后验分布时，常常使用数值方法，如马尔可夫链蒙特卡洛（MCMC）算法，它可以生成从后验分布中抽样的样本，从而对后验分布进行近似和推断。

## 2.3 贝叶斯推断的应用

### 2.3.1 参数估计

在统计模型中，参数估计是根据观测数据来估计模型参数的过程。贝叶斯推断提供了一种不同于传统频率主义方法的参数估计途径。在贝叶斯推断中，我们通过计算后验分布来得到参数的估计值，而不是单一的最佳估计值。

贝叶斯参数估计的核心在于后验分布，它是先验信念和新数据结合的结果。通过分析后验分布，我们可以得到参数的点估计、区间估计以及对参数不确定性的量化。

贝叶斯推断可以生成参数的完整后验分布，这使得我们不仅仅局限于给出一个点估计，还可以提供参数的不确定性度量，例如后验均值、中位数、置信区间等。此外，贝叶斯方法可以轻松地结合先验信息，这在许多实际问题中是非常有用的，尤其是在样本量较小的情况下。

### 2.3.2 模型比较与选择

模型选择是统计推断中的一个关键问题，贝叶斯推断提供了一种自然的方式来处理这一问题。贝叶斯方法使用后验概率作为评估模型优劣的准则，后验概率越高，模型被认为越优。在多个模型中选择时，贝叶斯因子（Bayes factor）是一个非常有用的工具。

贝叶斯因子是两个模型后验概率的比值，用来比较两个竞争模型的相对证据支持度：

\[ B_{12} = \frac{P(Data|M_1)}{P(Data|M_2)} \]

其中 \( M_1 \) 和 \( M_2 \) 是两个竞争模型，而 \( Data \) 是观测数据。贝叶斯因子的值可以告诉我们数据支持哪一个模型，或者哪一个模型更可能为真。贝叶斯因子的对数值（即log贝叶斯因子）通常在2以内，这表示正面证据支持；在2到6之间，表示中等证据支持；超过6则表示强证据支持。

除了贝叶斯因子，贝叶斯模型平均（Bayesian Model Averaging, BMA）也是模型选择的一种方法，它可以用来处理模型不确定性。BMA通过计算所有模型的加权平均来得到预测或估计，其中权重是各个模型的后验概率。通过这种方式，BMA提供了一种将模型不确定性纳入最终推断的途径。

# 3. 预防过拟合的贝叶斯策略

### 3.1 正则化方法

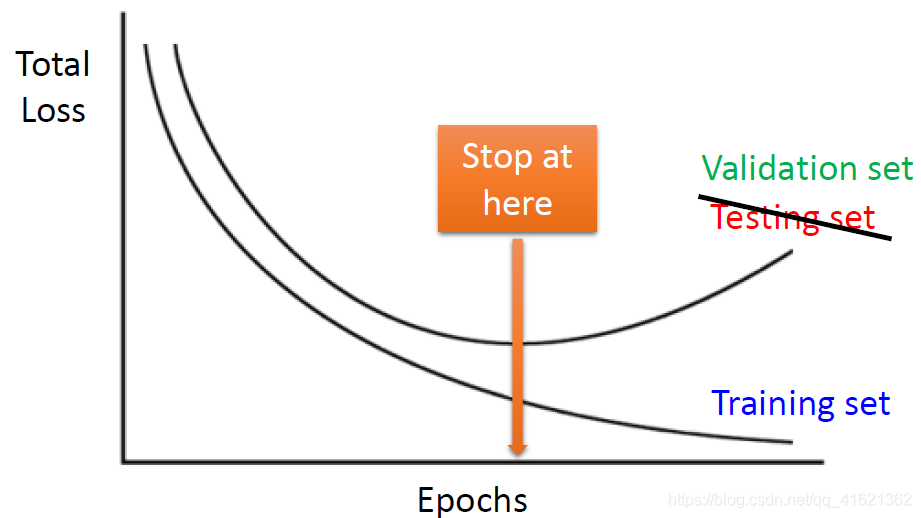
在机器学习和统计建模中，过拟合是一个常见问题，它发生在模型在训练数据上表现良好，但在新数据上表现不佳时。贝叶斯方法提供了一种强大的策略来预防过拟合，其核心思想是引入先验知识以限制模型复杂度，这就是贝叶斯正则化。

#### 3.1.1 贝叶斯正则化

贝叶斯正则化通过在模型参数上引入先验概率分布，以惩罚过于复杂的模型。这种先验可以是正态分布、拉普拉斯分布等，其参数（如正态分布的方差）控制了模型复杂度的容忍度。

例如，考虑一个线性回归模型，其参数向量为θ，数据集为D，先验p(θ)。根据贝叶斯定理，参数的后验分布是：

\[ p(θ|D) = \frac{p(D|θ)p(θ)}{p(D)} \]

其中，\( p(D|θ) \)是似然函数，\( p(θ) \)是参数的先验概率分布，\( p(D) \)是边缘概率（证据）。

代码块展示如何在代码中应用贝叶斯正则化：

import numpy as np
from scipy.stats import norm, laplace

# 假设线性模型参数向量theta和数据D
theta = np.random.randn(10) # 随机生成10个参数
D = np.random.randn(100) # 随机生成100个数据点

# 定义先验分布参数，例如使用正态分布
prior_mean = 0
prior_std = 1

# 定义后验分布的计算，这里简化为正态分布后验
posterior = norm(prior_mean, prior_std).pdf(theta)

# 计算数据的似然
likelihood = norm(theta.dot(D.T), 1).pdf(D)

# 应用贝叶斯公式计算后验分布
posterior = posterior * likelihood

# 归一化后验分布以得到概率密度函数
posterior /= np.sum(posterior)

# 输出后验分布值
print(posterior)

#### 3.1.2 超参数的贝叶斯推断

在贝叶斯正则化中，先验分布的参数（例如正态分布的均值和方差）是超参数。这些超参数可能需要根据具体任务进行调整，但也可以采用贝叶斯方法进行推断。

在进行贝叶斯推断时，可以通过评估后验分布来学习这些超参数。通常，这涉