R语言全面进阶指南：掌握数据处理至统计建模的15大技巧

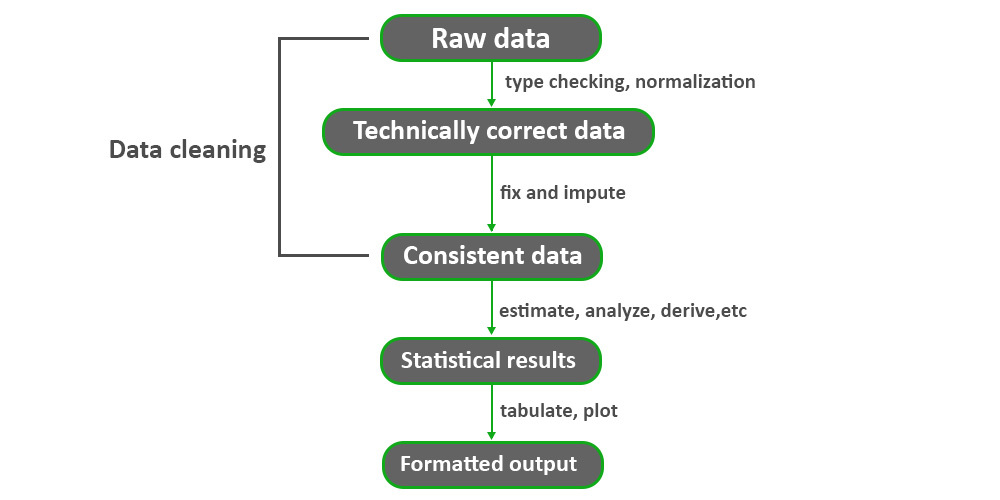
# 1. R语言简介与环境搭建

## R语言的起源与发展
R语言是一种用于统计分析和图形表示的编程语言，其设计思想源于S语言，并在1997年由Ross Ihaka和Robert Gentleman在新西兰奥克兰大学创建。经过多年的演进，R语言因其强大的社区支持、免费开源、丰富的包资源，以及在数据科学领域的广泛应用而受到全球研究者和开发者的青睐。

## R语言的核心优势
R语言之所以能在数据科学领域取得巨大成功，主要得益于以下核心优势：
- **免费开源**：任何人都可以免费下载、使用和分发R语言。
- **社区支持**：全球有数以千计的统计学家和数据科学家为其贡献包和文档。
- **统计功能强大**：内置了大量统计分析和图形绘制的函数，覆盖了大多数统计需求。
- **扩展性强**：通过CRAN（Comprehensive R Archive Network）等平台，用户可以安装第三方开发的包来扩展语言功能。
- **图形操作能力**：R语言提供了强大的绘图功能，能够生成高质量的图表，易于自定义和调整。

## 环境搭建与配置
在开始使用R语言之前，需要先完成环境的搭建。以下是详细的步骤：

1. **下载与安装**：访问R语言官方网站（***）下载对应操作系统的R语言安装包，并进行安装。
2. **安装RStudio（可选）**：RStudio是一个非常流行的R语言集成开发环境（IDE），它提供了更加友好的用户界面和额外的开发工具。访问RStudio官网（***）下载并安装RStudio。
3. **配置工作环境**：打开R或RStudio，安装需要的包和配置工作路径。以下是在R控制台中安装常用包的示例代码：

# 安装ggplot2包用于高级绘图
install.packages("ggplot2")
# 安装dplyr包用于数据处理
install.packages("dplyr")
# 安装tidyr包用于数据清洗
install.packages("tidyr")
# 加载安装好的包
library(ggplot2)
library(dplyr)
library(tidyr)

完成以上步骤后，你的R语言环境就配置完毕了。接下来，你可以开始探索R语言的基础知识和丰富的数据分析功能。

# 2. R语言数据处理技巧

### 2.1 基础数据类型与结构

#### 2.1.1 向量、矩阵和数组的操作

在R语言中，向量是最基本的数据结构，用于存储数值、字符等元素的序列。向量可以使用`c()`函数创建，例如创建一个包含数字1到5的向量：

vector <- c(1, 2, 3, 4, 5)

矩阵是二维的数值结构，可以使用`matrix()`函数创建。需要注意的是，矩阵中的元素必须是同一数据类型。创建一个3行2列的矩阵示例如下：

matrix <- matrix(1:6, nrow = 3, ncol = 2)

数组是多维的，可以视为一个包含矩阵的列表，使用`array()`函数创建。数组的维度通过`dim`参数指定，如创建一个2x3x4的数组：

array <- array(1:24, dim = c(2, 3, 4))

对这些基础结构的操作是数据分析的核心，包括索引、修改和维度调整等。例如，可以通过索引方式选取矩阵的子集：

sub_matrix <- matrix[1:2, 1] # 提取矩阵的第一列的前两个元素

向量、矩阵和数组的维度设置需要注意，因为它们在数据处理中起到了不同的作用。理解它们之间的关系和转换，对于优化数据处理流程至关重要。例如，一个矩阵可以看作是一个二维数组，而一个向量实际上是只有一维的数组。

#### 2.1.2 数据框(Data Frame)的高级处理

数据框(Data Frame)是R中最重要的数据结构之一，它可以存储不同类型的数据（数值、字符、因子等），并且其结构类似于数据库中的表格。数据框可以使用`data.frame()`函数创建：

df <- data.frame(
  id = 1:5,
  name = c("Alice", "Bob", "Charlie", "David", "Eve"),
  score = c(95, 82, 88, 79, 91)
)

数据框的高级处理涉及数据的分组、汇总、合并等操作。例如，使用`dplyr`包可以方便地进行数据框操作：

library(dplyr)

# 根据id对数据框进行分组，并计算每组的平均分数
grouped_scores <- df %>%
  group_by(id) %>%
  summarise(mean_score = mean(score))

数据框中的数据类型转换也是重要技能。使用`type.convert()`函数可以在读取数据时自动转换数据类型，也可以使用`as.*()`系列函数进行显式转换。例如，将字符型的id列转换为数值型：

df$id <- as.numeric(as.character(df$id))

数据框支持行和列的添加、删除以及子集的选取等操作。对数据框的操作需要综合考虑效率和代码的可读性，因为数据框是分析数据时最常处理的数据结构。例如，删除某列可以直接使用`-`符号：

df_sub <- df[, -3] # 删除第三列

### 2.2 数据清洗与预处理

#### 2.2.1 缺失数据的处理方法

在实际的数据分析中，经常会遇到数据缺失的情况。处理缺失数据的方法主要有删除含有缺失值的行或列、填充缺失值以及使用模型预测缺失值等。

R语言中，可以使用`na.omit()`函数删除含有缺失值的行：

clean_data <- na.omit(df) # 删除所有含有NA的行

也可以使用`complete.cases()`函数保留完整的数据行：

complete_data <- df[complete.cases(df), ]

对于填充缺失值，可以使用均值、中位数、众数或者模型预测的方法。例如，使用列的均值填充缺失值：

for (i in 1:ncol(df)) {
  df[is.na(df[, i]), i] <- mean(df[, i], na.rm = TRUE)
}

#### 2.2.2 数据的归一化和标准化

数据归一化和标准化通常是为了消除不同量纲的影响，使得数据更适合用于计算和模型分析。归一化将数据缩放到0-1区间，而标准化通常指的是将数据转换为均值为0、标准差为1的形式。

以下是将数据标准化的R代码示例：

# 标准化数据
standardized_data <- scale(df[, -which(names(df) == "id")])

# 查看标准化后的数据
print(standardized_data)

标准化的`scale()`函数也可以用于归一化：

# 归一化数据
normalized_data <- scale(df[, -which(names(df) == "id")], scale = FALSE)

#### 2.2.3 数据的变换和编码

数据的变换和编码是数据预处理的重要步骤。变换可以是取对数、平方根、指数等，而编码则是将分类数据转换为数值表示。

数据变换的示例如下：

# 对score列取对数变换
df$log_score <- log(df$score)

# 对score列取平方根变换
df$sqrt_score <- sqrt(df$score)

分类变量的编码：

# 假设name是分类变量，我们使用model.matrix()函数进行独热编码
one_hot_encoded <- model.matrix(~ name - 1, data = df)

数据的变换和编码都需要根据数据的特点和分析目标来合理选择。例如，对数变换常用于处理偏态数据，而独热编码用于处理类别数据。

### 2.3 数据探索性分析

#### 2.3.1 基本统计量的计算

在数据探索性分析阶段，计算基本统计量是了解数据分布特征的基础。R语言提供了丰富的方法来计算描述性统计量，如均值、中位数、方差、标准差等。

计算基本统计量的代码示例如下：

# 计算平均分数
mean_score <- mean(df$score)

# 计算分数的中位数
median_score <- median(df$score)

# 计算分数的标准差
sd_score <- sd(df$score)

对于不同分组的数据，可以使用`aggregate()`函数计算每个组的统计量：

# 按照name分组，计算每个组的平均分数
grouped_mean <- aggregate(score ~ name, data = df, FUN = mean)

#### 2.3.2 数据的可视化技巧

数据可视化是探索性分析的核心。在R语言中，`ggplot2`是一个非常强大的可视化包，它允许用户通过语法灵活地定制图形。

使用`ggplot2`绘制直方图的代码示例如下：

library(ggplot2)

# 绘制score的直方图
ggplot(df, aes(x = score)) + 
  geom_histogram(binwidth = 5, fill = "blue", color = "black") +
  labs(title = "Histogram of Scores", x = "Score", y = "Frequency")

绘制箱线图来展示数据分布的代码示例如下：

# 绘制每个name对应的score的箱线图
ggplot(df, aes(x = name, y = score)) +
  geom_boxplot(fill = "green") +
  labs(title = "Boxplot of Scores by Name", x = "Name", y = "Score")

#### 2.3.3 相关性分析与假设检验

在数据探索性分析中，经常需要进行相关性分析，以了解变量之间的关系强度和方向。R中可以使用`cor()`函数计算相关系数：

# 计算score与log_score之间的相关系数
correlation <- cor(df$score, df$log_score)

进行假设检验是了解变量间关系显著性的常用方法。例如，使用`t.test()`函数进行两个独立样本的t检验：

# 假设检验：检验男女学生的分数是否存在显著差异
male_scores <- df$score[df$name == "Bob"]
female_scores <- df$score[df$name == "Alice"]

t_test_result <- t.test(male_scores, female_scores)
print(t_test_result)

在实际应用中，常常需要根据数据的特性和分析目标选择合适的检验方法。例如，对于分类数据，可能需要使用卡方检验等非参数检验方法。

在本章节中，我们已经详细介绍了R语言中数据处理的一些基本技巧，包括对数据类型和结构的操作，数据的清洗和预处理方法，以及探索性分析的基本思路和技巧。掌握这些内容将为进行更深入的数据分析打下坚实的基础。接下来的章节将进一步深入到统计建模以及进阶分析方法中，探索数据背后的更多规律和知识。

# 3. R语言统计建模基础

## 3.1 常用统计分布与假设检验
统计分布是统计学中的核心概念，它描述了随机变量的概率特性。理解不同的统计分布可以帮助我们更好地理解数据的自然变异性，而假设检验则是统计建模中验证数据或模型推论是否符合预期的重要方法。

### 3.1.1 连续与离散分布的应用

#### 连续分布
在统计学中，连续分布描述了连续随机变量取各种可能值的概率。连续分布包括但不限于正态分布(Normal Distribution)、均匀分布(Uniform Distribution)和指数分布(Exponential Distribution)。这些分布经常在自然和社会科学领域中被用来模拟各种现象。

例如，正态分布在自然界和社会现象中极为常见，它的特征是均值(mean)和标准差(standard deviation)可以完全描述其形态，其数学表达式为：
\[ f(x|\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
其中，\( \mu \) 为均值，\( \sigma \) 为标准差。

#### 离散分布
相对地，离散分布描述的是随机变量取有限或可数无限多个值的概率。常见的离散分布有二项分布(Binomial Distribution)、泊松分布(Poisson Distribution)等。

以二项分布为例，它描述的是在固定次数的独立实验中，成功次数的概率分布，其概率质量函数为：
\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]
其中，\( n \) 是实验次数，\( k \) 是成功的次数，\( p \) 是单次实验成功的概率。

### 3.1.2 参数与非参数检验的区别

#### 参数检验
参数检验是基于总体参数已知的假设下进行的检验，最典型的参数检验包括t检验和卡方检验。参数检验通常要求数据满足一定的分布条件，例如正态分布，并且对数据的方差等参数有一定假设。t检验常用于比较两组数据的均值是否存在显著差异。

#### 非参数检验
当数据不符合特定的分布假设或者样本量太小时，非参数检验提供了一种无需对数据分布做出假设的检验方法。例如，曼-惠特尼U检验(Mann-Whitney U test)是一种用于比较两个独立样本是否来自相同分布的非参数检验方法。

非参数检验的灵活性更高，但相对参数检验，它的检验功效(即检测实际差异的能力)通常较低。在选择使用参数检验还是非参数检验时，需要综合考虑数据的分布特征、样本量大小以及检验功效的要求。

## 3.2 线性回归模型

### 3.2.1 简单线性回归的构建与解释

简单线性回归是最基本的统计建模形式，旨在研究两个变量之间的关系，其中一个变量被设定为因变量(Y)，另一个变量作为自变量(X)。简单的线性回归模型可以表达为：
\[ Y = \beta_0 + \beta_1X + \epsilon \]
这里，\( \beta_0 \) 是截距，\( \beta_1 \) 是斜率，而\( \epsilon \) 表示误差项。

在R语言中，使用`lm()`函数可以构建简单线性回归模型。例如，我们有数据集`cars`，包含速度和停车距离，我们可以建立速度和停车距离之间的线性关系：

data(cars)
model <- lm(dist ~ speed, data = cars)
summary(model)

通过`summary()`函数，我们能够获得回归模型的详细统计信息，如斜率的估计值、截距、R方值、F统计量、p值等。斜率系数表示速度每增加一个单位，停车距离预期增加的量。

### 3.2.2 多元线性回归分析与变量选择

在现实应用中，往往多个变量会影响目标变量。多元线性回归模型扩展了简单线性模型，允许同时考虑多个自变量(X1, X2, ..., Xn)对因变量(Y)的影响：
\[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n + \epsilon \]

多元线性回归的模型选择可以使用逐步回归(Stepwise Regression)方法，包括前进选择法、向后消除法和双向选择法。R语言中的`step()`函数可以根据AIC准则或BIC准则自动选择模型中的变量。

例如，考虑一个包含多个房屋特征数据集，我们想了解各特征如何影响房屋价格，我们可以这样构建多元线性回归模型：

# 假设已有数据集 housing_data
model <- lm(price ~ ., data = housing_data)
model_step <- step(model, direction = "both")
summary(model_step)

通过`step()`函数，我们得到一个考虑了多个变量的模型，并通过模型的摘要可以了解各个变量对房屋价格的影响。

## 3.3 分类与回归树(CART)

### 3.3.1 决策树模型的原理与实现

决策树模型是机器学习中的一种非参数监督学习方法，用于分类和回归。分类与回归树(CART)是一种常见的决策树算法，它可以处理不同类型的响应变量，不仅仅是分类问题。

CART模型通过一系列的分割规则将数据集划分为更小的子集，从而建立一个树状结构。每个内部节点代表对某个特征的一次测试，每个分支代表测试的一个结果，而每个叶节点代表一个分类或回归结果。

在R中，`rpart`包提供了构建CART模型的函数。以下是一个简单的示例，展示如何使用CART模型对鸢尾花数据集进行分类：

library(rpart)
data(iris)
iris_fit <- rpart(Species ~ ., data = iris, method = "class")

这段代码会训练一个决策树模型来预测鸢尾花的种类。

### 3.3.2 树模型的剪枝与优化

树模型可能会非常复杂，包括大量的分支，这可能会导致模型过度拟合训练数据。为了克服这个问题，CART提供了两种剪枝技术：预剪枝和后剪枝。

预剪枝是在构建决策树时提前停止树的增长，例如限定树的最大深度、叶节点的最小样本数或特征的最小分割数。后剪枝则是先生成一棵完整的树，然后从树中删除一些分支，以简化模型。

iris_pruned <- rpart(Species ~ ., data = iris, method = "class", control = rpart.control(minsplit = 10))

在这段代码中，`minsplit` 参数定义了分割一个节点所需的最小样本数，这有助于控制树的增长，减少过拟合。

以上是本章内容的概述，下面将深入分析R语言的高级统计建模方法，为读者提供更加深入的理解和应用指导。

# 4. R语言进阶分析方法

## 4.1 高级统计模型

### 4.1.1 广义线性模型(GLM)

广义线性模型（Generalized Linear Model, GLM）是统计建模中的一个重要扩展，它包括了线性回归、逻辑回归等多种统计模型。在R语言中，我们通常使用`glm()`函数来拟合GLM。GLM与传统的线性回归模型的主要区别在于其响应变量可以不必是正态分布，而是服从指数分布族。

GLM的一般形式如下：

Y = Xβ + ε

其中，Y是响应变量，X是解释变量矩阵，β是模型参数向量，ε是误差项。

GLM的三个主要部分是：

- 随机成分：描述响应变量Y的概率分布，可以是正态、二项、泊松等分布。
- 系统成分：描述解释变量X与响应变量Y之间的线性关系。
- 联接函数：用于连接随机成分的期望值（μ）和系统成分，允许因变量和自变量之间是非线性关系。

下面是一个GLM在R中的应用例子：

# 使用glm函数拟合逻辑回归模型
glm_model <- glm(response_variable ~ predictor1 + predictor2, 
                  family = binomial(link = "logit"), 
                  data = my_data)

该模型中，`response_variable`是二值响应变量，`predictor1`和`predictor2`是解释变量。`family = binomial(link = "logit")`指定了响应变量的分布为二项分布，联接函数为逻辑斯蒂函数。

在实际应用中，GLM特别适合于响应变量是二项或计数数据的情况，例如信贷违约预测、疾病发生率分析等。

### 4.1.2 混合效应模型与固定效应模型

混合效应模型（Mixed Effects Models）和固定效应模型（Fixed Effects Models）是处理分层数据的两种主要方法。这两种模型在R语言中可以使用`lme4`包中的`lmer()`函数和`lm()`函数来实现。

#### 混合效应模型

混合效应模型包含固定效应和随机效应两部分。固定效应关注解释变量的平均水平效应，而随机效应则允许组内差异可以被模型化。混合效应模型适合于研究数据具有明显层次结构的情况。

# 拟合混合效应模型示例
library(lme4)
mixed效应模型 <- lmer(response_variable ~ fixed_effects + (1 | random_effect), data = my_data)

#### 固定效应模型

固定效应模型专门用来分析解释变量中的组内效应，常用于面板数据或重复测量数据。其目的是消除不随时间变化的不可观测因素的影响。

# 拟合固定效应模型示例
fixed效应模型 <- lm(response_variable ~ fixed_effects + factor(group_id), data = my_data)

在上面的代码中，`group_id`是用来识别不同组别的变量，`factor(group_id)`确保组别以因子形式被模型识别。

这些模型在社会科学、生物统计学和经济学中有广泛的应用，特别是在处理嵌套数据结构时。通过正确地指定随机效应和固定效应，研究者能够更准确地估计解释变量对响应变量的影响，同时控制组内和组间的变化。

## 4.2 时间序列分析

### 4.2.1 ARIMA模型的基础与应用

自回归积分滑动平均模型（Autoregressive Integrated Moving Average，ARIMA）是时间序列分析中最常用的一种统计模型。ARIMA模型结合了自回归（AR）模型、差分处理和滑动平均（MA）模型，用于分析和预测时间序列数据。

#### ARIMA模型组成

- AR部分：描述了当前值与过去的值之间的线性关系。
- I部分：通过对时间序列进行差分来使其平稳化。
- MA部分：包含了时间序列值与其误差项之间的关系。

#### ARIMA模型选择

ARIMA模型的选择依赖于时间序列数据的特征，包括平稳性测试、自相关函数（ACF）和偏自相关函数（PACF）图来确定模型参数p和q，以及差分次数d。

#### R中的ARIMA模型应用

在R中，我们可以使用`forecast`包中的`auto.arima()`函数来自动化ARIMA模型的选择过程：

# 加载forecast包
library(forecast)

# 自动选择ARIMA模型并拟合
auto_arima_model <- auto.arima(my_time_series_data)

# 查看模型摘要
summary(auto_arima_model)

在得到拟合好的模型后，可以使用`forecast()`函数来进行预测：

# 预测未来10个时间点的值
future_forecast <- forecast(auto_arima_model, h = 10)
plot(future_forecast)

ARIMA模型常用于金融时间序列分析、天气预测、销售数据分析等领域。

### 4.2.2 季节性调整与预测

季节性调整是时间序列分析中的一个重要概念，其目的是从数据中分离出季节性成分，以便更清晰地看到趋势和其他非季节性的周期性成分。在R中，`forecast`包提供了`decompose()`函数来进行季节性调整：

# 对时间序列进行季节性调整
seasonally_adjusted <- decompose(my_time_series_data, type = "multiplicative")

季节性调整后，我们可以使用已经拟合好的ARIMA模型来进行未来时间点的预测，并考虑到季节性因素：

# 结合季节性因素进行预测
seasonal_arima <- auto.arima(my_time_series_data)
seasonal_forecast <- forecast(seasonal_arima, h = seasonal_period)
plot(seasonal_forecast)

季节性预测在商业、经济、环境科学等领域的决策制定过程中具有重要的应用价值。

## 4.3 机器学习算法实现

### 4.3.1 支持向量机(SVM)的原理与实践

支持向量机（Support Vector Machine, SVM）是一种强大的监督学习方法，用于分类和回归分析。其核心思想是寻找数据中能最大化不同类别间间隔的超平面。在R中，我们可以使用`e1071`包中的`svm()`函数来实现SVM。

#### SVM原理简述

- **超平面**：在高维空间中，将不同类别数据分开的平面。
- **间隔**：最靠近超平面的数据点叫做支持向量，支持向量之间的距离叫做间隔。
- **核函数**：通过非线性映射，把原始数据映射到高维空间，使数据在高维空间可被线性分割。

#### SVM在R中的应用

使用`svm()`函数构建分类器的基本流程如下：

# 加载e1071包
library(e1071)

# 使用SVM构建分类器
svm_model <- svm(training_data, 
                 target_variable, 
                 kernel = "radial", 
                 cost = 10, 
                 gamma = 0.1)

# 进行预测
predicted_classes <- predict(svm_model, test_data)

# 检查预测准确性
table(predicted_classes, actual_classes)

在SVM中，`kernel`参数可以为`linear`、`polynomial`、`radial`或`sigmoid`等，用于定义数据映射的核函数。`cost`和`gamma`参数是调整模型复杂度的关键超参数。

SVM在手写识别、面部识别、生物信息学等领域拥有广泛的应用。

### 4.3.2 随机森林与梯度提升树的应用

随机森林（Random Forest）和梯度提升树（Gradient Boosting Trees，GBT）是两种流行的集成学习方法，它们通过构建多个决策树并组合它们的预测来提高准确性和稳定性。

#### 随机森林

随机森林在R中通过`randomForest`包实现：

# 加载randomForest包
library(randomForest)

# 使用随机森林构建模型
rf_model <- randomForest(training_data, 
                         target_variable, 
                         ntree = 500, 
                         mtry = 3)

# 对测试数据集进行预测
rf_predictions <- predict(rf_model, test_data)

# 模型评估
confusionMatrix(rf_predictions, test_data$target_variable)

在上述代码中，`ntree`参数指定了要构建的树的数量，`mtry`参数表示在分裂节点时考虑的随机变量的数量。

#### 梯度提升树

梯度提升树在R中可以通过`gbm`包实现：

# 加载gbm包
library(gbm)

# 使用梯度提升树构建模型
gbm_model <- gbm(target_variable ~ ., 
                 data = training_data, 
                 n.trees = 500, 
                 interaction.depth = 4, 
                 shrinkage = 0.01, 
                 cv.folds = 5)

# 对测试数据进行预测
gbm_predictions <- predict(gbm_model, test_data, n.trees = 500)

# 模型评估
# 需要定义适当的误差度量方法来评估模型性能

在`gbm()`函数中，`n.trees`参数指定树的数量，`interaction.depth`参数指定树的最大深度，`shrinkage`参数用于控制学习速率，`cv.folds`参数用于指定交叉验证的折数。

随机森林和梯度提升树在金融风险评估、生物信息学特征选择、广告点击率预测等领域表现优异。

在本章中，我们学习了R语言中几种重要的进阶分析方法，包括广义线性模型、混合效应模型和固定效应模型、时间序列分析中的ARIMA模型及其季节性调整，以及随机森林和梯度提升树这两种集成学习方法。这些方法在统计建模和机器学习领域有着广泛的应用，并通过实践案例加深了理论知识的理解。在掌握这些高级分析方法之后，您将能够应对更复杂的数据分析挑战。

# 5. R语言在实际项目中的应用

## 5.1 数据可视化与报告制作

在数据分析和科学报告中，数据可视化是一项至关重要的技能。R语言以其丰富的可视化包而受到广泛使用，其中`ggplot2`包因其强大的定制能力和美观的图表而出名。此外，`Shiny`是一个特别强大的交互式Web应用框架，允许用户通过简单的R脚本创建动态的Web应用和报告。

### 5.1.1 ggplot2高级图表定制

`ggplot2`是基于“图层”的设计，这使得用户可以按照数据、几何对象、统计变换和图形属性的顺序来构建图表。通过组合不同的图层，我们可以创建出各种各样的数据可视化图表。

**示例代码展示如何使用ggplot2绘制一个散点图：**

library(ggplot2)

# 假设我们有一个名为df的数据框，包含变量x, y, group
# 绘制散点图
ggplot(df, aes(x=x, y=y, color=group)) +
  geom_point() +
  labs(title="散点图示例",
       x="X轴标题",
       y="Y轴标题",
       color="分组变量")

在这个示例中，我们首先加载了`ggplot2`包，然后使用`ggplot()`函数来设定基础图层，并通过`geom_point()`添加了散点层。`labs()`函数用于添加图表的标题和坐标轴标签。

### 5.1.2 动态报告与交互式应用Shiny

`Shiny`是一个用于创建交互式Web应用的强大工具。它允许R用户创建无需HTML、CSS或JavaScript知识的Web应用。一个典型的`Shiny`应用包含两个主要部分：`ui.R`和`server.R`。`ui.R`定义了应用的用户界面，而`server.R`包含了应用的业务逻辑。

**简单Shiny应用的代码示例：**

# ui.R
shinyUI(fluidPage(
  titlePanel("我的Shiny应用"),
  sidebarLayout(
    sidebarPanel(
      sliderInput("bins",
                  "Number of bins:",
                  min = 1,
                  max = 50,
                  value = 30)
    ),
    mainPanel(
      plotOutput("distPlot")
    )
  )

# server.R
shinyServer(function(input, output) {
  output$distPlot <- renderPlot({
    x    <- faithful[, 2] 
    bins <- seq(min(x), max(x), length.out = input$bins + 1)
    hist(x, breaks = bins, col = 'darkgray', border = 'white')
  })
})

在这个示例中，`ui.R`定义了一个包含滑动条的侧边栏和一个主面板，主面板将显示直方图。`server.R`则定义了如何根据输入的滑动条值来绘制直方图。

## 5.2 大数据环境下的R语言应用

随着数据集的规模日益庞大，传统的数据处理方法已不能满足需求。因此，R语言也开始与大数据技术如Hadoop和Spark集成，提供了新的解决方案。

### 5.2.1 R与Hadoop/Spark的集成

R语言通过多种方式与Hadoop和Spark集成，包括`RHadoop`和`SparkR`包。这些包允许数据科学家使用熟悉的R语言对大数据进行处理。

**示例：使用`Rhadoop`包读取HDFS数据：**

# 安装并加载Rhadoop相关包
# install.packages("rmr2")
library(rmr2)

# 读取HDFS上的文件
hdfs <- hdfs.init()
hdfsText <- from.dfs(hdfs, "/path/to/file.txt")

# 进行数据处理
mapreduce(input=hdfsText,
          map = function(k, v) cbind(v, 1),
          reduce = function(k, vs) keyval(k, length(vs)))

# 清理HDFS资源
hdfs.close(hdfs)

在这个例子中，我们首先加载`rmr2`包，然后初始化HDFS连接。之后，我们从HDFS读取文本文件，并使用`mapreduce`函数进行映射和归约操作。最后，我们关闭HDFS连接以释放资源。

### 5.2.2 分布式计算与性能优化技巧

在处理大数据时，性能优化至关重要。在R中，有多种方法可以提高计算性能，包括使用C/C++的Rcpp包，使用并行计算的`parallel`包，或者使用专门的大数据处理包如`sparklyr`。

**示例：使用`sparklyr`包进行Spark的DataFrame操作：**

# 安装并加载sparklyr包
# install.packages("sparklyr")
library(sparklyr)

sc <- spark_connect(master = "local")

# 读取数据到Spark
iris_tbl <- copy_to(sc, iris, "iris")

# 使用dplyr语法进行数据操作
library(dplyr)
result <- iris_tbl %>%
  filter(Species == "versicolor") %>%
  select(Petal.Length, Petal.Width) %>%
  collect()

spark_disconnect(sc)

在这个例子中，我们首先建立了与Spark集群的连接，然后将iris数据集复制到Spark环境。接着，我们使用`dplyr`语法对数据进行过滤和选择，最后收集结果并断开连接。

## 5.3 R包的开发与管理

随着项目复杂性的增加，如何管理和维护R包变得至关重要。R包的开发不仅仅是编写代码，还包括文档编写、单元测试和版本控制等。

### 5.3.1 开发流程与最佳实践

R包的开发通常遵循一系列最佳实践，包括代码的组织、编写文档和单元测试等。

- **代码组织：** 遵循`usethis`和`devtools`包提供的标准结构来组织代码。
- **文档编写：** 使用`roxygen2`注释来生成文档。
- **单元测试：** 利用`testthat`包来编写测试案例。

**示例：创建一个简单的R包骨架**

# 使用usethis包创建包的基本结构
# install.packages("usethis")
usethis::create_package("myPackage")

# 添加一个函数并使用roxygen2注释
myFunction <- function(x) {
  x * 2
}

usethis::use_r("myFunction")
roxygen2::roxygenize()

# 创建测试文件并写入测试案例
test_that("myFunction multiples by 2", {
  expect_equal(myFunction(2), 4)
})

在这个例子中，我们首先创建了一个名为`myPackage`的新包。然后，我们定义了一个简单的函数，并使用`roxygen2`注释添加文档。最后，我们使用`testthat`创建了一个测试案例。

### 5.3.2 包的测试、文档编写与版本控制

一旦R包开发完成，还需要进行测试和文档编写，以确保包的质量和用户友好性。此外，使用版本控制系统如`git`和`GitHub`来管理包的版本和进行协作是不可或缺的。

**示例：将R包推送到GitHub**

# 生成README.md
usethis::use_readme_rmd()

# 初始化git仓库
usethis::use_git()

# 将项目推送到GitHub
usethis::use_github()

在这个例子中，我们首先生成了`README`文件，然后初始化了git仓库，并最终将项目推送到GitHub上。

以上内容演示了如何在实际项目中应用R语言进行数据可视化与报告制作、大数据环境下的处理以及R包的开发与管理。这些实际应用案例和技巧将帮助R语言用户更有效地解决现实中的问题，提高工作效率和项目质量。