数据清洗中的排序算法应用：提升数据处理效率的利器

# 1. 数据清洗与排序算法的重要性

在现代数据处理的场景下，数据清洗与排序算法是两个不可分割的重要组成部分。数据清洗保证了数据的质量和可用性，是数据分析、机器学习以及其他数据密集型应用的基石。排序算法则是数据清洗过程中不可或缺的一环，它能够在数据排序、搜索和优化方面发挥关键作用。本章将探讨为何数据清洗和排序算法在数据处理中如此重要，以及它们如何相辅相成，共同促进数据的准确性和处理效率。

## 1.1 数据清洗与排序算法的协同作用

数据清洗旨在移除数据中的噪声、不一致性或无关信息，而排序算法则将数据按照特定顺序进行排列，以便于分析和处理。它们的协同作用体现在以下几点：

- **准确性提升**：通过清洗，数据的准确性和可靠性得到保证，排序算法则能够更加精确地处理这些高质量数据。
- **效率优化**：排序算法能够优化数据处理流程，例如在索引构建、查找和合并操作中发挥关键作用，从而提升整体的数据处理效率。
- **决策支持**：排序后，数据的可视化和解释能力增强，为业务决策提供更加有力的支持。

## 1.2 应用背景与实际需求

在大数据时代背景下，企业收集并存储了海量的数据，这些数据往往包含许多不完整、不准确或不一致的部分。数据清洗与排序算法的应用需求如下：

- **企业决策支持**：对于需要快速响应市场变化的企业而言，数据清洗和排序算法能够帮助快速分析数据，从而做出及时的商业决策。
- **业务流程优化**：在业务流程自动化和智能化的推动下，高效的数据清洗和排序能力是提升业务流程效率的关键。
- **新兴技术融合**：数据清洗和排序算法与其他新兴技术（如人工智能、物联网）的融合，为特定场景下的问题解决提供了新的可能性。

通过本章的探讨，我们将深入理解数据清洗与排序算法的重要性，并为后续章节中对排序算法的系统学习和应用案例分析打下坚实的基础。

# 2. ```
# 第二章：排序算法基础理论

## 2.1 排序算法的基本概念

### 2.1.1 排序的定义与目的

排序是将一组数据按照特定的顺序重新排列的过程。排序算法的目的是在数据集合中提供一个有序的序列，使得数据能够按照一定的规律进行快速的检索、分析、处理和传输。

从计算机科学的角度来看，排序算法是一种基本的计算机操作，广泛应用于数据库、搜索引擎、数据可视化等众多领域。排序算法不仅提高了数据处理的效率，同时也有助于提升用户体验，比如在搜索引擎中能够快速给出相关性高的结果。

### 2.1.2 时间复杂度与空间复杂度简介

时间复杂度和空间复杂度是衡量排序算法性能的两个关键指标。

- **时间复杂度**：主要用来衡量算法执行所需的时间，通常以算法的操作步骤数量与输入数据规模的函数关系来表示。常见的表示法包括O(n)、O(n log n)、O(n^2)等。

- **空间复杂度**：衡量算法在执行过程中临时占用存储空间大小的指标。排序算法中，有的需要额外的存储空间（如归并排序需要额外的数组空间），而有的不需要（如插入排序）。

理解这两个概念对于选择合适的排序算法至关重要，尤其是在资源受限的环境下，比如嵌入式系统或者大数据处理。

## 2.2 常见排序算法解析

### 2.2.1 冒泡排序和选择排序

- **冒泡排序**：通过重复遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。该算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

- **选择排序**：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

以下是冒泡排序的Python代码实现：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

# 测试数组
test_array = [64, 34, 25, 12, 22, 11, 90]

# 进行排序
bubble_sort(test_array)

print("排序后的数组:")
print(test_array)

在上述代码中，`bubble_sort` 函数通过双层循环遍历数组，进行两两比较并交换位置，最终输出排序后的数组。

### 2.2.2 插入排序和快速排序

- **插入排序**：构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

- **快速排序**：通过一个划分操作将数据分为独立的两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后再递归地对这两部分数据分别进行快速排序，以达到整个序列有序。

快速排序的Python代码示例：

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

# 测试数组
test_array = [3, 6, 8, 10, 1, 2, 1]

# 进行排序
sorted_array = quick_sort(test_array)

print("排序后的数组:")
print(sorted_array)

在上述代码中，`quick_sort` 函数通过递归方式将数组分割为小于基准值、等于基准值和大于基准值三部分，然后递归排序左右两部分，最终合并结果。

### 2.2.3 归并排序与堆排序

- **归并排序**：采用分治法的一个非常典型的应用，将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

- **堆排序**：利用堆这种数据结构所设计的一种排序算法。堆是一种近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。

堆排序的Python代码示例：

import heapq

def heap_sort(arr):
    heapq.heapify(arr)
    return [heapq.heappop(arr) for _ in range(len(arr))]

# 测试数组
test_array = [4, 10, 3, 5, 1]

# 进行排序
sorted_array = heap_sort(test_array)

print("排序后的数组:")
print(sorted_array)

在上述代码中，`heap_sort` 函数使用Python的`heapq`模块来实现堆排序，其中`heapq.heapify`方法用于将列表转换成一个堆结构，然后使用`heappop`方法依次弹出最小值元素，直到堆为空，得到排序后的数组。

## 2.3 排序算法的比较与选择

### 2.3.1 不同场景下的算法选择策略

选择合适的排序算法对于性能优化至关重要。以下是一些根据不同场景选择排序算法的策略：

- **对于小规模数据集**：可以考虑使用插入排序或者冒泡排序，因为它们简单且容易实现。

- **对于大规模数据集**：快速排序是最佳选择，因为它在平均情况下具有较好的时间复杂度（O(n log n)）。

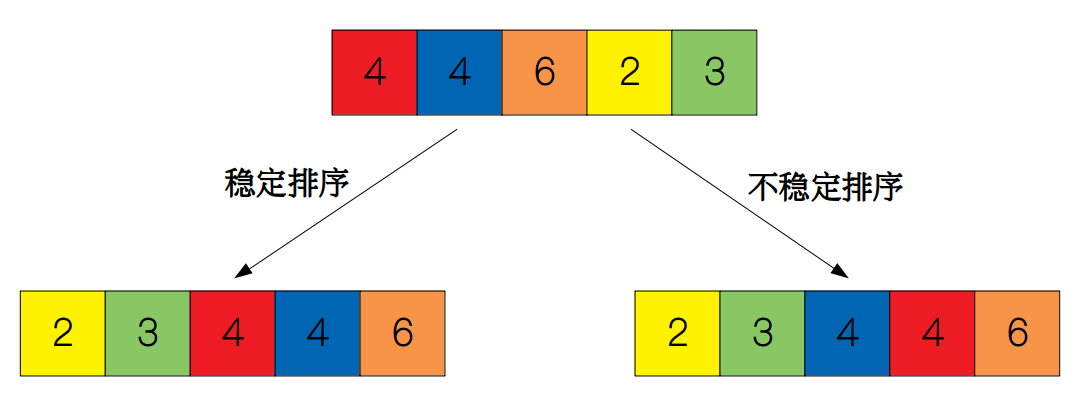
- **对于需要稳定排序的场景**：归并排序是不错的选择，因为它是稳定的，能够保持相等元素的相对顺序。

- **当内存空间受限时**：可以考虑原地排序算法，如快速排序。

### 2.3.2 算法的时间空间权衡

在选择排序算法时，需要考虑算法的时间和空间复杂度之间的权衡：

- **时间复杂度**：对于排序算法，时间复杂度是最重要的性能指标。如果数据集很大，优先选择时间复杂度较低的算法。

- **空间复杂度**：不同的排序算法在空间使用上有着不同的要求。在内存受限的情况下，应选择空间复杂度较低的排序算法，如原地排序算法。

以上是排序算法的基础理论知识。在实际应用中，对不同算法的深入理解和分析对于提升程序性能有着不可忽