揭秘线性表核心操作：增删查改，从入门到精通

# 1. 线性表的基本概念和操作

线性表是一种数据结构，它由一组有序的元素组成，每个元素都具有相同的数据类型。线性表中的元素之间存在着线性关系，即每个元素都与相邻的元素相连。线性表的基本操作包括增、删、查、改，这些操作可以实现对线性表中数据的有效管理。

### 1.1 线性表的特点

线性表具有以下特点：

- **有序性：**线性表中的元素是有序排列的，每个元素都有一个确定的位置。
- **线性关系：**线性表中的元素之间存在线性关系，即每个元素都与相邻的元素相连。
- **动态性：**线性表可以动态地增删元素，以适应数据的变化。

# 2. 线性表的增删查改操作

线性表的增删查改操作是线性表的基础操作，也是后续高级数据结构的基础。本章节将详细介绍线性表的增删查改操作的实现原理、时间复杂度和应用场景。

### 2.1 增：插入操作

插入操作是指在指定位置插入一个元素。线性表中常用的插入操作有三种：头插法、尾插法和指定位置插入。

#### 2.1.1 头插法

头插法是在线性表的头部插入一个元素。其算法步骤如下：

def insert_head(L, x):
    """在链表头部插入元素x"""
    p = Node(x)
    p.next = L.head
    L.head = p

**代码逻辑逐行解读：**

1. 创建一个新的节点p，并将其值设置为x。
2. 将新节点p的next指针指向链表的头部。
3. 将链表的头部指针指向新节点p。

**参数说明：**

* L：线性表对象
* x：要插入的元素

**时间复杂度：**O(1)

#### 2.1.2 尾插法

尾插法是在线性表的尾部插入一个元素。其算法步骤如下：

def insert_tail(L, x):
    """在链表尾部插入元素x"""
    p = Node(x)
    if L.head is None:
        L.head = p
    else:
        cur = L.head
        while cur.next is not None:
            cur = cur.next
        cur.next = p

**代码逻辑逐行解读：**

1. 创建一个新的节点p，并将其值设置为x。
2. 如果链表为空，则将新节点设置为链表的头部。
3. 否则，遍历链表找到最后一个节点，并将新节点插入到其后。

**参数说明：**

* L：线性表对象
* x：要插入的元素

**时间复杂度：**O(n)，其中n为链表的长度。

#### 2.1.3 指定位置插入

指定位置插入是在线性表的指定位置插入一个元素。其算法步骤如下：

def insert_at(L, index, x):
    """在链表指定位置index插入元素x"""
    if index == 0:
        insert_head(L, x)
    elif index == L.length:
        insert_tail(L, x)
    else:
        p = Node(x)
        cur = L.head
        for i in range(index - 1):
            cur = cur.next
        p.next = cur.next
        cur.next = p

**代码逻辑逐行解读：**

1. 如果index为0，则调用头插法插入元素。
2. 如果index为链表长度，则调用尾插法插入元素。
3. 否则，遍历链表找到第index个节点，并将其后一个节点指向新节点。

**参数说明：**

* L：线性表对象
* index：要插入的位置
* x：要插入的元素

**时间复杂度：**O(n)，其中n为链表的长度。

### 2.2 删：删除操作

删除操作是指删除指定位置的元素。线性表中常用的删除操作有三种：头删法、尾删法和指定位置删除。

#### 2.2.1 头删法

头删法是删除线性表的头部元素。其算法步骤如下：

def delete_head(L):
    """删除链表头部元素"""
    if L.head is None:
        return
    L.head = L.head.next

**代码逻辑逐行解读：**

1. 如果链表为空，则直接返回。
2. 将链表的头部指针指向下一个节点。

**参数说明：**

* L：线性表对象

**时间复杂度：**O(1)

#### 2.2.2 尾删法

尾删法是删除线性表的尾部元素。其算法步骤如下：

def delete_tail(L):
    """删除链表尾部元素"""
    if L.head is None:
        return
    if L.head.next is None:
        L.head = None
    else:
        cur = L.head
        while cur.next.next is not None:
            cur = cur.next
        cur.next = None

**代码逻辑逐行解读：**

1. 如果链表为空，则直接返回。
2. 如果链表只有一个元素，则将链表的头部指针指向None。
3. 否则，遍历链表找到最后一个节点，并将其前一个节点的next指针指向None。

**参数说明：**

* L：线性表对象

**时间复杂度：**O(n)，其中n为链表的长度。

#### 2.2.3 指定位置删除

指定位置删除是删除线性表的指定位置的元素。其算法步骤如下：

def delete_at(L, index):
    """删除链表指定位置index的元素"""
    if index == 0:
        delete_head(L)
    elif index == L.length - 1:
        delete_tail(L)
    else:
        cur = L.head
        for i in range(index - 1):
            cur = cur.next
        cur.next = cur.next.next

**代码逻辑逐行解读：**

1. 如果index为0，则调用头删法删除元素。
2. 如果index为链表长度减1，则调用尾删法删除元素。
3. 否则，遍历链表找到第index个节点，并将其后一个节点删除。

**参数说明：**

* L：线性表对象
* index：要删除的位置

**时间复杂度：**O(n)，其中n为链表的长度。

### 2.3 查：查找操作

查找操作是指在线性表中查找指定元素。线性表中常用的查找操作有两种：顺序查找和二分查找。

#### 2.3.1 顺序查找

顺序查找是从线性表的头部开始，逐个比较元素，直到找到目标元素或遍历完整个线性表。其算法步骤如下：

def sequential_search(L, x):
    """顺序查找元素x"""
    cur = L.head
    while cur is not None:
        if cur.val == x:
            return cur
        cur = cur.next
    return None

**代码逻辑逐行解读：**

1. 从线性表的头部开始遍历。
2. 比较当前元素的值与目标元素的值。
3. 如果相等，则返回当前元素。
4. 否则，继续遍历下一个元素。

**参数说明：**

* L：线性表对象
* x：要查找的元素

**时间复杂度：**O(n)，其中n为链表的长度。

#### 2.3.2 二分查找

二分查找适用于有序线性表。其算法步骤如下：

def binary_search(L, x):
    """二分查找元素x"""
    low = 0
    high = L.length - 1
    while low <= high:
        mid = (low + high) // 2
        if L[mid] == x:
            return mid
        elif L[mid] < x:
            low = mid + 1
        else:
            high = mid - 1
    return -1

**代码逻辑逐行解读：**

1. 初始化low和high指针，分别指向线性表的头部和尾部。
2. 循环执行以下步骤：
- 计算中间位置mid。
- 比较中间元素的值与目标元素的值。
- 如果相等，则返回中间位置。
- 如果中间元素的值小于目标元素的值，则将low指针移动到中间位置的下一个位置。
- 否则，将high指针移动到中间位置的前一个位置。
3. 如果循环结束时low指针大于high指针，则表示未找到目标元素，返回-1。

**参数说明：**

* L：有序线性表对象
* x：要查找的元素

**时间复杂度：**O(log n)，其中n为链表的长度。

### 2.4 改：修改操作

修改操作是指修改线性表中指定位置的元素。线性表中常用的修改操作有三种：头修改、尾修改和指定位置修改。

#### 2.4.1 头修改

头修改是修改线性表的头部元素。其算法步骤如下：

def modify_head(L, x):
    """修改链表头部元素为x"""
    if L.head is None:
        return
    L.head.val = x

**代码逻辑逐行解读：**

1. 如果链表为空，则直接返回。
2. 将链表头部元素的值修改为x。

**参数说明：**

* L：线性表对象
* x

# 3. 先进先出

**3.1.1 队列的实现**

队列是一种遵循先进先出（FIFO）原则的数据结构。这意味着最早进入队列的元素将首先被移除。队列可以基于数组或链表实现。

**基于数组的队列实现**

class Queue:
    def __init__(self, size):
        self.queue = [None] * size
        self.head = 0
        self.tail = 0

    def enqueue(self, item):
        if (self.tail + 1) % len(self.queue) == self.head:
            raise IndexError("Queue is full")
        self.queue[self.tail] = item
        self.tail = (self.tail + 1) % len(self.queue)

    def dequeue(self):
        if self.head == self.tail:
            raise IndexError("Queue is empty")
        item = self.queue[self.head]
        self.head = (self.head + 1) % len(self.queue)
        return item

**基于链表的队列实现**

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class Queue:
    def __init__(self):
        self.head = None
        self.tail = None

    def enqueue(self, item):
        new_node = Node(item)
        if self.tail is None:
            self.head = new_node
        else:
            self.tail.next = new_node
        self.tail = new_node

    def dequeue(self):
        if self.head is None:
            raise IndexError("Queue is empty")
        item = self.head.data
        self.head = self.head.next
        if self.head is None:
            self.tail = None
        return item

**3.1.2 队列的应用**

队列在实际应用中非常常见，例如：

- **消息队列：**用于在系统组件之间传递消息，确保消息按顺序处理。
- **任务队列：**用于管理需要按顺序执行的任务，如打印作业或电子邮件发送。
- **缓冲区：**用于在生产者和消费者之间提供缓冲，避免数据丢失。
- **广度优先搜索（BFS）：**用于遍历图或树，按层级顺序访问节点。

# 4. 线性表的复杂度分析

### 4.1 时间复杂度

时间复杂度描述算法执行所花费的时间，通常用大 O 符号表示。对于线性表，主要考虑以下操作的时间复杂度：

#### 4.1.1 顺序查找的时间复杂度

顺序查找从线性表的第一个元素开始，依次与目标元素进行比较，直到找到目标元素或遍历完整个线性表。其时间复杂度为 O(n)，其中 n 为线性表中元素的个数。

#### 4.1.2 二分查找的时间复杂度

二分查找适用于有序线性表。它通过不断将查找范围缩小一半，快速找到目标元素。其时间复杂度为 O(log n)。

#### 4.1.3 链表查找的时间复杂度

链表查找需要从头结点开始，依次遍历每个节点，直到找到目标元素或遍历完整个链表。其时间复杂度为 O(n)，其中 n 为线性表中元素的个数。

### 4.2 空间复杂度

空间复杂度描述算法执行所占用的内存空间。对于线性表，主要考虑以下操作的空间复杂度：

#### 4.2.1 数组实现的空间复杂度

数组实现的线性表需要预先分配一个固定大小的数组来存储元素。其空间复杂度为 O(n)，其中 n 为线性表中元素的个数。

#### 4.2.2 链表实现的空间复杂度

链表实现的线性表不需要预先分配内存空间，而是动态分配节点来存储元素。其空间复杂度为 O(n)，其中 n 为线性表中元素的个数。

### 4.2.3 复杂度分析表格

| 操作 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 顺序查找 | O(n) | O(n) |
| 二分查找 | O(log n) | O(n) |
| 链表查找 | O(n) | O(n) |

### 4.3 复杂度优化

为了优化线性表的复杂度，可以采用以下策略：

* **选择合适的线性表实现方式：**对于顺序查找，数组实现优于链表实现；对于二分查找，链表实现优于数组实现。
* **使用索引：**为线性表建立索引可以快速定位目标元素，从而优化查找操作的时间复杂度。
* **使用分治算法：**将线性表划分为多个子表，并分别进行查找操作，可以优化查找操作的时间复杂度。
* **使用缓存：**将最近访问过的元素缓存起来，可以优化后续查找操作的时间复杂度。

# 5. 线性表的扩展和优化

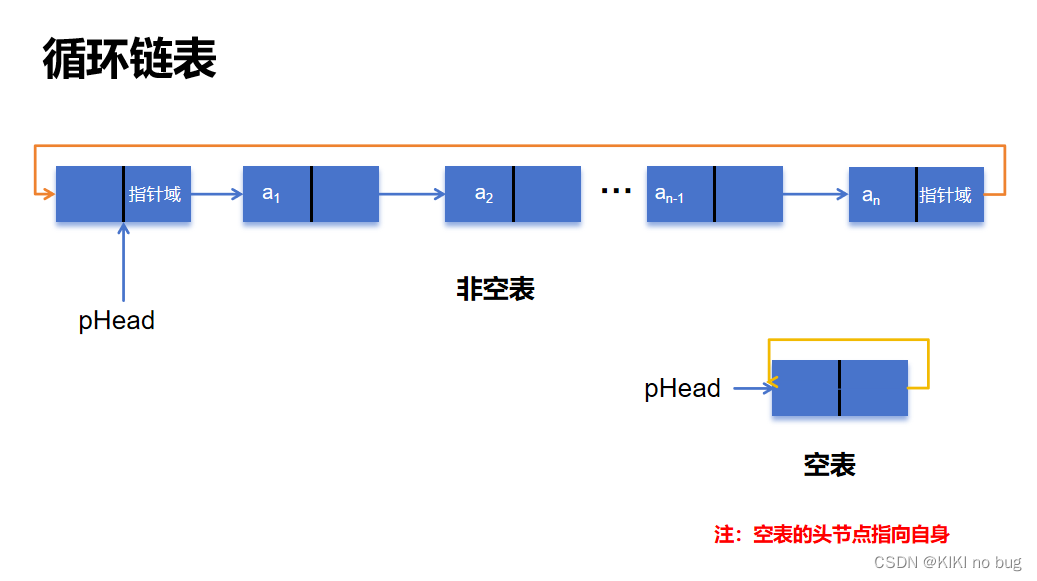
### 5.1 循环链表

#### 5.1.1 循环链表的实现

循环链表是在单链表的基础上，将尾结点的 next 指针指向头结点，形成一个闭合的环形结构。这样，循环链表可以从任意一个结点开始遍历，并且可以方便地插入和删除结点。

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class CircularLinkedList:
    def __init__(self):
        self.head = None

    def insert_at_beginning(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            new_node.next = self.head
        else:
            new_node.next = self.head
            current = self.head
            while current.next != self.head:
                current = current.next
            current.next = new_node
            self.head = new_node

    def insert_at_end(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            new_node.next = self.head
        else:
            current = self.head
            while current.next != self.head:
                current = current.next
            current.next = new_node
            new_node.next = self.head

    def insert_at_position(self, data, position):
        new_node = Node(data)
        if position == 0:
            self.insert_at_beginning(data)
        else:
            current = self.head
            count = 0
            while current.next != self.head and count < position - 1:
                current = current.next
                count += 1
            if count == position - 1:
                new_node.next = current.next
                current.next = new_node
            else:
                print("Invalid position")

    def delete_at_beginning(self):
        if self.head is None:
            print("List is empty")
        else:
            current = self.head
            while current.next != self.head:
                current = current.next
            current.next = self.head.next
            self.head = self.head.next

    def delete_at_end(self):
        if self.head is None:
            print("List is empty")
        else:
            current = self.head
            while current.next.next != self.head:
                current = current.next
            current.next = self.head

    def delete_at_position(self, position):
        if self.head is None:
            print("List is empty")
        else:
            current = self.head
            count = 0
            while current.next != self.head and count < position - 1:
                current = current.next
                count += 1
            if count == position - 1:
                current.next = current.next.next
            else:
                print("Invalid position")

    def display(self):
        current = self.head
        while current.next != self.head:
            print(current.data, end=" ")
            current = current.next
        print(current.data)

#### 5.1.2 循环链表的应用

循环链表的应用场景包括：

* **约瑟夫环问题：**解决一个圆形队列中，从某个位置开始报数，报到某个数的人出列的问题。
* **哈希表：**使用循环链表作为哈希表中的冲突解决机制，可以有效减少冲突的发生。
* **缓冲区：**使用循环链表作为缓冲区，可以实现数据的循环读写，提高数据处理效率。

### 5.2 双向链表

#### 5.2.1 双向链表的实现

双向链表是在单链表的基础上，为每个结点添加一个 prev 指针，指向其前驱结点。这样，双向链表可以双向遍历，并且可以方便地插入和删除结点。

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None

class DoublyLinkedList:
    def __init__(self):
        self.head = None
        self.tail = None

    def insert_at_beginning(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            self.tail = new_node
        else:
            new_node.next = self.head
            self.head.prev = new_node
            self.head = new_node

    def insert_at_end(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            self.tail = new_node
        else:
            new_node.prev = self.tail
            self.tail.next = new_node
            self.tail = new_node

    def insert_at_position(self, data, position):
        new_node = Node(data)
        if position == 0:
            self.insert_at_beginning(data)
        elif position == self.get_length():
            self.insert_at_end(data)
        else:
            current = self.head
            count = 0
            while current.next is not None and count < position - 1:
                current = current.next
                count += 1
            if count == position - 1:
                new_node.next = current.next
                current.next.prev = new_node
                current.next = new_node
                new_node.prev = current
            else:
                print("Invalid position")

    def delete_at_beginning(self):
        if self.head is None:
            print("List is empty")
        else:
            if self.head == self.tail:
                self.head = None
                self.tail = None
            else:
                self.head = self.head.next
                self.head.prev = None

    def delete_at_end(self):
        if self.head is None:
            print("List is empty")
        else:
            if self.head == self.tail:
                self.head = None
                self.tail = None
            else:
                self.tail = self.tail.prev
                self.tail.next = None

    def delete_at_position(self, position):
        if self.head is None:
            print("List is empty")
        elif position == 0:
            self.delete_at_beginning()
        elif position == self.get_length() - 1:
            self.delete_at_end()
        else:
            current = self.head
            count = 0
            while current.next is not None and count < position - 1:
                current = current.next
                count += 1
            if count == position - 1:
                current.next = current.next.next
                current.next.prev = current
            else:
                print("Invalid position")

    def get_length(self):
        count = 0
        current = self.head
        while current is not None:
            count += 1
            current = current.next
        return count

    def display(self):
        current = self.head
        while current is not None:
            print(current.data, end=" ")
            current = current.next
        print()

#### 5.2.2 双向链表的应用

双向链表的应用场景包括：

* **LRU 缓存：**使用双向链表作为 LRU 缓存的实现，可以快速访问最近使用的数据。
* **浏览器历史记录：**使用双向链表作为浏览器的历史记录，可以方便地向前和向后浏览。
* **文本编辑器：**使用双向链表作为文本编辑器的文本缓冲区，可以高效地进行文本编辑和操作。

### 5.3 跳表

#### 5.3.1 跳表的实现

跳表是一种基于链表实现的概率数据结构，它通过引入多个层次的指针来提高查找效率。跳表中的结点除了包含数据和 next 指针外，还包含多个 level 指针，指向更高层次的结点。

import random

class Node:
    def __init__(self, data, level):
        self.data = data
        self.next = [None] * level

class SkipList:
    def __init__(self, p=0.5):
        self.header = Node(None, 1)
        self.

# 6. 线性表在实际项目中的应用

### 6.1 数据结构的选择

在实际项目中，选择合适的线性表数据结构对于优化性能和代码简洁性至关重要。以下是一些常见的比较：

#### 6.1.1 数组与链表的比较

| 特征 | 数组 | 链表 |
|---|---|---|
| 存储方式 | 连续内存块 | 分散内存块 |
| 访问方式 | 索引访问 | 指针访问 |
| 插入删除 | 复杂度高 | 复杂度低 |
| 空间利用率 | 高 | 低 |
| 适用场景 | 数据量固定，频繁索引 | 数据量可变，频繁插入删除 |

#### 6.1.2 队列与栈的比较

| 特征 | 队列 | 栈 |
|---|---|---|
| 进出顺序 | 先进先出 (FIFO) | 后进先出 (LIFO) |
| 适用场景 | 处理顺序数据，如消息队列 | 处理嵌套结构数据，如函数调用 |

### 6.2 常见算法的实现

线性表在实际项目中广泛用于实现各种算法。以下是一些常见的示例：

#### 6.2.1 排序算法

* 冒泡排序
* 选择排序
* 插入排序
* 快速排序
* 归并排序

#### 6.2.2 搜索算法

* 顺序查找
* 二分查找
* 哈希查找

#### 6.2.3 图形算法

* 广度优先搜索 (BFS)
* 深度优先搜索 (DFS)
* 最小生成树 (MST)
* 最短路径 (Dijkstra 算法)