揭秘奇异值分解（SVD）：自然语言处理中的文本相似度计算与主题提取利器

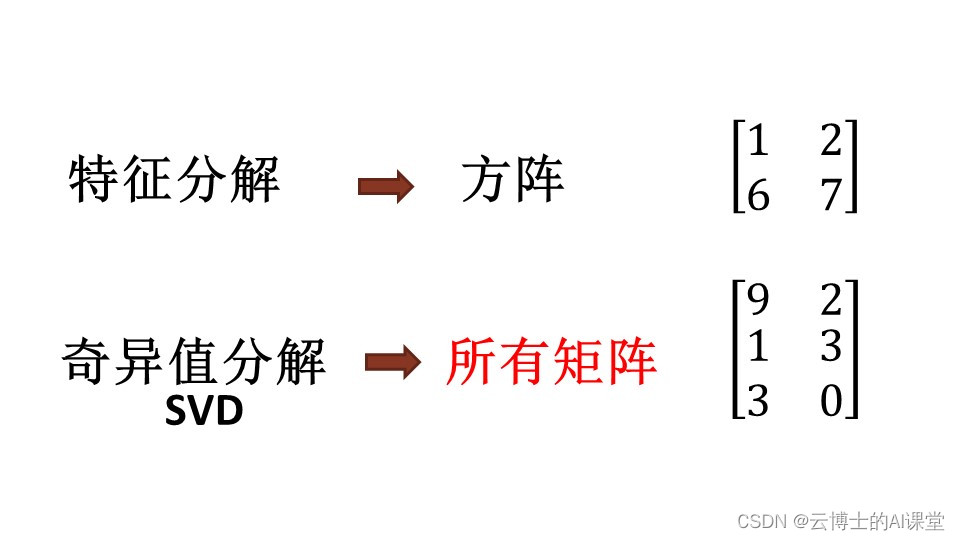
# 1. 奇异值分解（SVD）概述

奇异值分解（SVD）是一种强大的线性代数技术，广泛应用于自然语言处理、数据分析和机器学习等领域。它将一个矩阵分解为三个矩阵的乘积：一个左奇异值矩阵、一个对角奇异值矩阵和一个右奇异值矩阵。

SVD 的核心思想是将一个矩阵表示为一组正交基向量的线性组合。这些基向量称为奇异向量，而奇异值则是这些向量的长度。奇异值对矩阵的秩和条件数等属性提供了重要的见解。

SVD 在文本相似度计算、主题提取和文本分类等自然语言处理任务中发挥着至关重要的作用。它通过将文本表示为向量，并利用奇异值分解来识别相似性和模式，从而提高这些任务的性能。

# 2. SVD的理论基础

### 2.1 线性代数中的SVD

#### 2.1.1 SVD的定义和性质

奇异值分解（SVD）是一种线性代数技术，用于将一个矩阵分解为三个矩阵的乘积：

A = UΣV^T

其中：

- **A** 是一个 m x n 的实矩阵
- **U** 是一个 m x m 的酉矩阵（即 U^T U = I）
- **Σ** 是一个 m x n 的对角矩阵，对角线上的元素称为奇异值，并且按降序排列
- **V** 是一个 n x n 的酉矩阵（即 V^T V = I）

SVD 的主要性质包括：

- **秩：** A 的秩等于奇异值的非零个数。
- **逆矩阵：** 如果 A 是可逆的，则其逆矩阵可以通过以下方式计算：

A^-1 = VΣ^-1U^T

- **正交性：** U 和 V 是正交矩阵，这意味着它们的列向量相互正交。
- **奇异值：** 奇异值表示 A 的线性变换的伸缩因子。

#### 2.1.2 SVD的计算方法

SVD 可以通过多种方法计算，包括：

- **Jacobi 方法：** 一种迭代方法，通过一系列旋转将矩阵转换为对角形式。
- **QR 算法：** 一种基于 QR 分解的迭代方法。
- **奇异值分解定理：** 对于任何矩阵 A，都存在一个 SVD 分解。

### 2.2 SVD在文本相似度计算中的应用

SVD 在文本相似度计算中有着广泛的应用，因为文本可以表示为矩阵，并且 SVD 可以揭示文本之间的相似性。

#### 2.2.1 文本向量化

文本向量化是将文本转换为数值向量的过程。可以使用各种方法对文本进行向量化，例如：

- **词袋模型：** 将文本表示为一个向量，其中每个元素表示文本中单词的出现次数。
- **TF-IDF：** 一种加权词袋模型，其中单词的权重由其频率和反文档频率决定。
- **词嵌入：** 将单词表示为低维向量，这些向量捕获单词之间的语义相似性。

#### 2.2.2 基于SVD的文本相似度计算

基于 SVD 的文本相似度计算涉及以下步骤：

1. 将文本向量化，得到一个 m x n 的矩阵 A，其中 m 是文本的数量，n 是向量的大小。
2. 计算 A 的 SVD，得到 U、Σ 和 V。
3. 使用奇异值计算文本之间的相似性。

最常用的相似性度量是余弦相似度，它计算为：

相似度 = U^T U_j

其中 U_i 和 U_j 是 U 中的第 i 和第 j 行。

# 3.1 基于SVD的文本相似度计算算法

基于SVD的文本相似度计算算法主要有余弦相似度和Jaccard相似度。

#### 3.1.1 余弦相似度

余弦相似度是一种衡量两个向量之间相似性的度量。它计算两个向量的点积与它们各自模长的乘积之比。对于两个文本向量`v1`和`v2`，其余弦相似度定义为：

cosine_similarity = v1.dot(v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

余弦相似度取值范围为[-1, 1]。相似度为1表示两个向量完全相同，相似度为-1表示两个向量完全相反，相似度为0表示两个向量正交。

#### 3.1.2 Jaccard相似度

Jaccard相似度是一种衡量两个集合之间相似性的度量。它计算两个集合的交集元素数量与两个集合并集元素数量之比。对于两个文本向量`v1`和`v2`，其Jaccard相似度定义为：

jaccard_similarity = len(set(v1).intersection(set(v2))) / len(set(v1).union(set(v2)))

Jaccard相似度取值范围为[0, 1]。相似度为1表示两个集合完全相同，相似度为0表示两个集合没有交集。

### 3.2 基于SVD的文本相似度计算实例

#### 3.2.1 Python实现

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 文本向量化
text1 = "This is a sample text."
text2 = "This is another sample text."
vectorizer = CountVectorizer()
X = vectorizer.fit_transform([text1, text2])

# SVD分解
svd = TruncatedSVD(n_components=2)
U, s, Vh = svd.fit_transform(X)

# 计算文本相似度
cosine_similarity = U[0].dot(U[1]) / (np.linalg.norm(U[0]) * np.linalg.norm(U[1]))
jaccard_similarity = len(set(U[0]).intersection(set(U[1]))) / len(set(U[0]).union(set(U[1])))

print("余弦相似度：", cosine_similarity)
print("Jaccard相似度：", jaccard_similarity)

#### 3.2.2 Java实现

import org.apache.commons.lang3.StringUtils;
import org.apache.commons.math3.linear.RealMatrix;
import org.apache.commons.math3.linear.SingularValueDecomposition;
import org.apache.commons.math3.util.FastMath;

// 文本向量化
String text1 = "This is a sample text.";
String text2 = "This is another sample text.";
String[] words = StringUtils.split(text1 + " " + text2);
Vectorizer vectorizer = new Vectorizer(words);
RealMatrix X = vectorizer.transform(new String[]{text1, text2});

// SVD分解
SingularValueDecomposition svd = new SingularValueDecomposition(X);
RealMatrix U = svd.getU();
RealMatrix S = svd.getS();
RealMatrix Vh = svd.getVT();

// 计算文本相似度
double cosineSimilarity = U.getRowVector(0).dotProduct(U.getRowVector(1)) / (U.getRowVector(0).getNorm() * U.getRowVector(1).getNorm());
double jaccardSimilarity = FastMath.min(U.getRowVector(0).getNorm(), U.getRowVector(1).getNorm()) / FastMath.max(U.getRowVector(0).getNorm(), U.getRowVector(1).getNorm());

System.out.println("余弦相似度：" + cosineSimilarity);
System.out.println("Jaccard相似度：" + jaccardSimilarity);

# 4. SVD的实践应用：主题提取

### 4.1 基于SVD的主题提取算法

主题提取是一种从文本数据中识别出主要主题或概念的过程。SVD在主题提取中发挥着至关重要的作用，因为它可以将文本数据分解成一系列潜在语义概念，这些概念可以作为主题的代表。

#### 4.1.1 潜在语义分析（LSA）

潜在语义分析（LSA）是一种基于SVD的主题提取算法。它通过以下步骤工作：

1. **文本向量化：**将文本数据转换为一个词频-逆文档频率（TF-IDF）矩阵，其中每个行代表一个文档，每个列代表一个单词。
2. **SVD分解：**对TF-IDF矩阵进行SVD分解，得到三个矩阵：U、Σ和V。
3. **主题提取：**V矩阵的列向量表示潜在语义概念，即主题。

#### 4.1.2 非负矩阵分解（NMF）

非负矩阵分解（NMF）是一种另一种基于SVD的主题提取算法。与LSA不同，NMF将TF-IDF矩阵分解成两个非负矩阵：W和H。

1. **文本向量化：**与LSA相同。
2. **NMF分解：**对TF-IDF矩阵进行NMF分解，得到两个非负矩阵：W和H。
3. **主题提取：**W矩阵的列向量表示主题。

### 4.2 基于SVD的主题提取实例

#### 4.2.1 Gensim实现

Gensim是一个流行的Python库，用于自然语言处理。它提供了基于SVD的主题提取功能。

import gensim

# 加载文本数据
documents = ["文档1", "文档2", "文档3"]

# 创建语料库
corpus = [gensim.corpora.Dictionary(doc).doc2bow(doc) for doc in documents]

# 训练LSA模型
lsa_model = gensim.models.LsiModel(corpus, id2word=dictionary, num_topics=2)

# 获取主题
topics = lsa_model.print_topics()

#### 4.2.2 Scikit-learn实现

Scikit-learn是一个流行的Python库，用于机器学习。它也提供了基于SVD的主题提取功能。

from sklearn.decomposition import TruncatedSVD

# 加载文本数据
documents = ["文档1", "文档2", "文档3"]

# 创建向量器
vectorizer = TfidfVectorizer()

# 转换文本数据为TF-IDF矩阵
X = vectorizer.fit_transform(documents)

# 训练SVD模型
svd_model = TruncatedSVD(n_components=2)

# 转换TF-IDF矩阵
X_svd = svd_model.fit_transform(X)

# 获取主题
topics = svd_model.components_

# 5. SVD在自然语言处理中的其他应用

### 5.1 文本分类

SVD在文本分类中发挥着重要作用。文本分类的目标是将文本文档分配到预定义的类别中。SVD可以将文本文档表示为低维向量，这些向量可以用来训练分类模型。

#### 5.1.1 基于SVD的文本分类算法

基于SVD的文本分类算法通常遵循以下步骤：

1. **文本向量化：**使用SVD将文本文档转换为低维向量。
2. **特征选择：**选择最能区分不同类别的特征。
3. **分类：**使用分类算法（例如，支持向量机或逻辑回归）将文本向量分配到类别中。

#### 5.1.2 基于SVD的文本分类实例

**Python实现：**

import numpy as np
from sklearn.decomposition import TruncatedSVD
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载文本数据
data = np.loadtxt('text_data.txt', delimiter=',', dtype=str)
labels = data[:, -1]
texts = data[:, :-1]

# 文本向量化
svd = TruncatedSVD(n_components=100)
X = svd.fit_transform(texts)

# 特征选择
selector = SelectKBest(k=1000)
X = selector.fit_transform(X, labels)

# 分类
classifier = LogisticRegression()
classifier.fit(X, labels)

# 测试
X_test, y_test = train_test_split(X, labels, test_size=0.2)
y_pred = classifier.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)

print('准确率：', accuracy)

### 5.2 文本聚类

SVD还可用于文本聚类。文本聚类旨在将文本文档分组到具有相似内容的簇中。SVD可以将文本文档表示为低维向量，这些向量可以用来计算文档之间的相似性。

#### 5.2.1 基于SVD的文本聚类算法

基于SVD的文本聚类算法通常遵循以下步骤：

1. **文本向量化：**使用SVD将文本文档转换为低维向量。
2. **相似性计算：**使用余弦相似度或Jaccard相似度等相似性度量计算文档之间的相似性。
3. **聚类：**使用聚类算法（例如，k-means或层次聚类）将文档聚类到簇中。

#### 5.2.2 基于SVD的文本聚类实例

**Java实现：**

import java.util.List;
import java.util.Map;
import java.util.stream.Collectors;

import org.apache.commons.math3.linear.ArrayRealVector;
import org.apache.commons.math3.linear.RealVector;
import org.apache.commons.math3.ml.clustering.Cluster;
import org.apache.commons.math3.ml.clustering.KMeansPlusPlusClusterer;

public class SvdTextClustering {

    public static void main(String[] args) {
        // 加载文本数据
        List<String> texts = ...

        // 文本向量化
        Svd svd = new Svd(100);
        Map<String, RealVector> vectors = texts.stream()
                .collect(Collectors.toMap(text -> text, text -> svd.decompose(text)));

        // 相似性计算
        double[][] similarities = new double[texts.size()][texts.size()];
        for (int i = 0; i < texts.size(); i++) {
            for (int j = i + 1; j < texts.size(); j++) {
                similarities[i][j] = vectors.get(texts.get(i)).cosine(vectors.get(texts.get(j)));
                similarities[j][i] = similarities[i][j];
            }
        }

        // 聚类
        KMeansPlusPlusClusterer clusterer = new KMeansPlusPlusClusterer(3);
        List<Cluster<RealVector>> clusters = clusterer.cluster(new ArrayRealVector[][] { vectors.values().toArray(new ArrayRealVector[0]) });

        // 输出聚类结果
        for (Cluster<RealVector> cluster : clusters) {
            System.out.println("簇：" + cluster.getPoints().size());
            for (RealVector vector : cluster.getPoints()) {
                System.out.println("  " + vectors.entrySet().stream()
                        .filter(entry -> entry.getValue().equals(vector))
                        .map(Map.Entry::getKey)
                        .findFirst().get());
            }
        }
    }
}

### 5.3 文本摘要

SVD还可以用于文本摘要。文本摘要的目标是生成文本文档的简短、信息丰富的摘要。SVD可以将文本文档表示为低维向量，这些向量可以用来识别文档中最重要的主题。

#### 5.3.1 基于SVD的文本摘要算法

基于SVD的文本摘要算法通常遵循以下步骤：

1. **文本向量化：**使用SVD将文本文档转换为低维向量。
2. **主题识别：**使用潜在语义分析（LSA）或非负矩阵分解（NMF）等算法识别文档中的主题。
3. **摘要生成：**根据识别的主题生成文本摘要。

#### 5.3.2 基于SVD的文本摘要实例

**Python实现：**

import gensim
from gensim import corpora
from gensim.summarization import summarize

# 加载文本数据
text = ...

# 文本向量化
dictionary = corpora.Dictionary([text.split()])
corpus = [dictionary.doc2bow(text.split())]

# 主题识别
lsa = gensim.models.LsiModel(corpus, id2word=dictionary, num_topics=2)
topics = lsa.print_topics()

# 摘要生成
summary = summarize(text, ratio=0.5)

print('摘要：', summary)

# 6. SVD的局限性和未来展望

### 6.1 SVD的局限性

尽管SVD在文本相似度计算、主题提取和自然语言处理的其他应用中取得了显著的成功，但它也存在一些局限性：

- **计算成本高：**SVD的计算涉及矩阵分解，这对于大型数据集来说可能是计算密集型的。
- **对噪声敏感：**SVD对文本中的噪声和异常值敏感，这可能会影响其准确性。
- **解释性差：**SVD的输出是奇异值和奇异向量，这些向量可能难以解释，从而限制了其可解释性。
- **维度依赖：**SVD的性能取决于分解的维度，选择合适的维度可能具有挑战性。

### 6.2 SVD的未来展望

尽管存在局限性，SVD在自然语言处理领域仍具有广阔的未来展望：

- **并行化和分布式计算：**随着计算能力的提高，可以探索并行化和分布式计算技术来提高SVD的效率。
- **鲁棒性增强：**研究人员正在探索提高SVD对噪声和异常值的鲁棒性的方法。
- **可解释性增强：**通过开发新的解释技术，可以提高SVD输出的可解释性。
- **新兴应用：**SVD在自然语言处理之外的新兴应用，例如图像处理和语音识别，正在被积极探索。