鲁棒控制应对电机控制中的不确定性：策略与应用，让电机系统稳如磐石

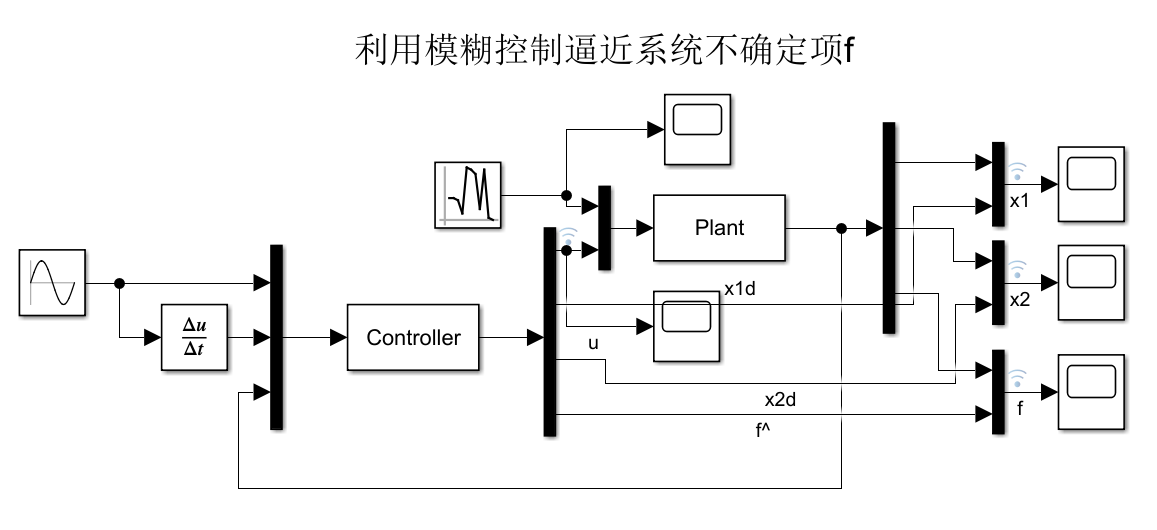
# 1. 电机控制中的不确定性

电机控制系统不可避免地存在不确定性，包括：

- **参数不确定性：**电机参数（如电感、电阻）受温度、老化等因素影响而变化。
- **负载不确定性：**负载的惯量、摩擦力等特性可能未知或随时间变化。
- **环境不确定性：**温度、湿度等环境因素会影响电机性能。

这些不确定性会影响控制系统的稳定性和性能，导致电机无法准确跟踪指令，甚至出现振荡或失稳现象。因此，鲁棒控制策略对于电机控制系统至关重要，以应对这些不确定性。

# 2.1 滑模控制

### 2.1.1 滑模控制的基本原理

滑模控制是一种非线性控制方法，它通过设计一个滑动面，使系统状态在滑动面上滑行，从而实现对系统的鲁棒控制。滑动面的设计目标是使系统在滑动面上的运动具有期望的动态特性，例如稳定性、鲁棒性和快速响应。

滑模控制的基本原理如下：

1. **定义滑动面：**设计一个滑动面 $s(x, t) = 0$，其中 $x$ 是系统状态，$t$ 是时间。滑动面通常是一个超平面，它将状态空间划分为两个部分。
2. **到达条件：**设计一个控制律 $u(x, t)$，使系统状态 $x$ 沿着滑动面运动，即 $\dot{s} = 0$。
3. **保持条件：**一旦系统状态到达滑动面，控制律 $u(x, t)$ 应确保系统状态保持在滑动面上，即 $s(x, t) = 0$。

### 2.1.2 滑模控制器的设计

滑模控制器的设计包括以下步骤：

1. **选择滑动面：**滑动面的选择取决于系统的具体要求和性能目标。常用的滑动面包括线性滑动面、非线性滑动面和高阶滑动面。
2. **设计等效控制：**等效控制 $u_{eq}(x, t)$ 是在滑动面上使系统状态保持运动的控制律。等效控制的计算方法有Lyapunov稳定性理论、积分分离法和高阶滑模控制等。
3. **设计切换控制：**切换控制 $u_{sw}(x, t)$ 是使系统状态到达滑动面的控制律。切换控制的计算方法有边界层法、饱和函数法和高阶滑模控制等。
4. **总控律：**总控律 $u(x, t)$ 是等效控制和切换控制的组合，即 $u(x, t) = u_{eq}(x, t) + u_{sw}(x, t)$。

**代码块：**

import numpy as np

def sliding_mode_controller(x, t):
    """
    滑模控制器

    参数：
        x: 系统状态
        t: 时间

    返回：
        控制律
    """

    # 定义滑动面
    s = x[0] + x[1]

    # 设计等效控制
    u_eq = -x[1]

    # 设计切换控制
    u_sw = -np.sign(s)

    # 计算总控律
    u = u_eq + u_sw

    return u

**逻辑分析：**

该代码块实现了滑模控制器的设计。首先，定义了滑动面 $s = x[0] + x[1]$。然后，计算了等效控制 $u_{eq} = -x[1]$ 和切换控制 $u_{sw} = -np.sign(s)$。最后，计算了总控律 $u = u_{eq} + u_{sw}$。

**参数说明：**

* `x`: 系统状态，是一个包含系统位置和速度的列表。
* `t`: 时间，是一个标量。
* `u`: 控制律，是一个标量。

# 3. 鲁棒控制在电机控制中的应用

鲁棒控制策略在电机控制领域有着广泛的应用，特别是在存在不确定性和干扰的情况下。本章节将介绍鲁棒控制在电机位置控制和速度控制中的应用，并探讨其优势和局限性。

### 3.1 位置控制

**3.1.1 滑模控制在位置控制中的应用**

滑模控制是一种鲁棒控制技术，通过将系统状态限制在预定义的滑模表面上来实现控制目标。在电机位置控制中，滑模