【SVPWM算法在实时系统中的挑战与对策】:优化与实现难点
发布时间: 2024-11-30 17:40:15 阅读量: 24 订阅数: 37 


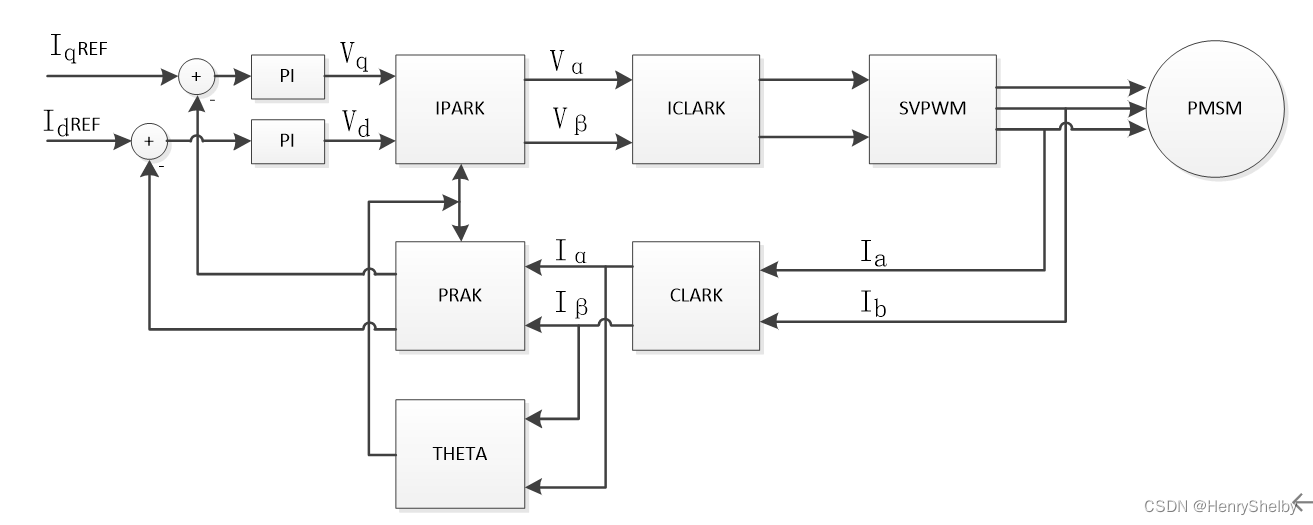
单片机与DSP中的用单片机实现SVPWM合成
参考资源链接:[SVPWM原理详解:推导、控制算法及空间电压矢量特性](https://wenku.csdn.net/doc/7g8nyekbbp?spm=1055.2635.3001.10343)
# 1. SVPWM算法概述
空间矢量脉宽调制(SVPWM)是一种高效的电力电子开关控制技术,广泛应用于电机驱动、变频器和可再生能源等领域。其核心在于通过优化开关序列和时间分配,减少逆变器输出电流的谐波含量,提高整体性能。SVPWM算法基于电机或逆变器的三相对称模型,将开关状态映射到一个复平面上,形成多个空间矢量。通过控制这些空间矢量的合成和作用时间,实现对输出电压的有效控制。这一算法的优化和实现对现代电力电子设备的效率和性能至关重要。下面章节将进一步探讨SVPWM算法的理论基础、实现挑战、优化策略和应用案例,为读者提供全面的技术洞见。
# 2. SVPWM算法理论基础
## 2.1 空间矢量理论
空间矢量理论是理解SVPWM算法的起点,它为算法提供了理论基础和实现框架。理解这一理论对于深入分析SVPWM算法至关重要。
### 2.1.1 空间矢量调制的基本原理
空间矢量调制(Space Vector Modulation,SVM)是一种用于多电平逆变器的PWM技术,通过在时间平均上合成期望的输出电压矢量来控制电机。基本原理是利用电压矢量的合成和分解,将电机控制问题转化为空间矢量的控制问题。这一过程可以形象地理解为在复平面上移动矢量,以此来近似一个圆形或椭圆形的旋转矢量。
关键步骤包括:
1. 确定合成矢量:基于电机的控制指令(如转矩和磁通),确定所需的参考矢量。
2. 分解合成矢量:将参考矢量分解为相邻的三个基本矢量(实际存在或者虚拟生成的)。
3. 计算矢量作用时间:通过几何关系或优化算法计算各个基本矢量的作用时间。
4. 实现矢量切换:根据计算出的作用时间切换逆变器的状态,从而合成所需的参考矢量。
### 2.1.2 矢量扇区的划分与判断方法
为了方便矢量的合成和切换,需要将整个复平面划分为不同的扇区。SVPWM算法中的矢量扇区通常是六个,对应于逆变器开关状态的六种基本组合。每个扇区由相邻的三个基本矢量界定,并且每个矢量对应一个扇区。
判断参考矢量位于哪个扇区的方法通常涉及基本矢量的叉乘或点积运算。例如,给定三个基本矢量 V1, V2, 和 V3,可以通过以下逻辑判断参考矢量 Vref 所在的扇区:
```
if (Vref.x * V1.y - Vref.y * V1.x >= 0) {
if (Vref.x * V2.y - Vref.y * V2.x < 0)
扇区 = 1;
else
扇区 = 6;
} else {
if (Vref.x * V3.y - Vref.y * V3.x < 0)
扇区 = 2;
else
扇区 = 5;
}
```
其中,Vref.x 和 Vref.y 是参考矢量在复平面上的坐标,V1.x, V1.y, V2.x, V2.y, V3.x, V3.y 分别为三个基本矢量在复平面上的坐标。
## 2.2 SVPWM算法的数学模型
### 2.2.1 SVPWM数学描述
SVPWM算法的数学模型是基于空间矢量和基本矢量的数学表示,它为实现控制策略提供了精确的数学工具。数学模型中,通常将逆变器的三相输出电压表示为一个复数或二维矢量,并在复平面上进行操作。
数学模型的关键公式包括:
- 逆变器输出电压矢量 Vout = (Vout_a + jVout_b)/sqrt(3)
- 基本矢量 V1, V2, V3 等的表示
- 参考矢量 Vref 的表示
- 各基本矢量作用时间的计算
### 2.2.2 矢量作用时间的计算方法
在SVPWM算法中,计算基本矢量作用时间是核心步骤。这通常涉及到以下方程:
```
T1 = (2Vref.x + Vref.y)/sqrt(3) * T
T2 = 2Vref.y/sqrt(3) * T
T0 = T - (T1 + T2)
```
其中,T1和T2是相邻两个基本矢量的作用时间,T0是零矢量的作用时间,T是开关周期。以上计算使用了三个基本矢量对应的电压值和参考矢量的坐标。
## 2.3 SVPWM与传统PWM的比较
### 2.3.1 PWM调制技术概述
传统PWM调制技术通常基于方波调制,通过调整波形的占空比来控制输出电压的平均值。SVPWM则是一种优化的PWM调制技术,它在复平面内对电压矢量进行操作,不仅考虑了输出电压的幅值,还考虑了输出电压相位的信息,从而能够更精细地控制电机。
### 2.3.2 SVPWM的优势分析
SVPWM相较于传统PWM技术的优势主要体现在以下几个方面:
1. **提高直流母线利用率**:SVPWM在相同的开关频率下,可以输出更高的基波电压幅值。
2. **减少开关损耗**:由于电压矢量在空间中更接近圆形轨迹,因此开关次数相对于传统PWM技术有所减少。
3. **改善输出波形**:SVPWM输出波形更加接近正弦波,可以降低电机的谐波损耗和噪音。
4. **增加有效矢量数目**:SVPWM算法可以增加有效矢量的使用,从而提高电机控制的精确度。
本章节详细介绍了SVPWM算法的基础理论,为后续章节中算法在实时系统中的实现挑战、优化策略以及在实际应用中的案例分析提供了扎实的理论支撑。接下来的章节将继续深入探讨这些方面。
# 3. SVPWM算法在实时系统中的实现挑战
实现SVPWM算法在实时系统中是电力电子领域的一个技术挑战。实时系统对于时间的敏感性要求算法必须在严格的时序约束下完成复杂的计算任务。本章节将深入探讨SVPWM算法在实时系统中实现所面临的挑战。
## 3.1 实时性能要求
### 3.1.1 实时系统的特点与要求
实时系统(Real-Time System, RTS)被广泛应用于工业控制、航空航天和汽车电子等领域,它的核心要求在于对事件或数据的处理必须满足特定的时间约束。实时系统通常分为两类:硬实时系统和软实时系统。硬实时系统必须严格按照时间约束完成任务,否则可能会导致灾难性的后果;而软实时系统则可以容忍一定的延迟,但仍然要求在可接受的时间范围内完成任务。
在SVPWM算法的应用中,实时系统需要在每个PWM周期内计算出相应的开关状态,这就要求算法不仅要准确还要快速。SVPWM算法的实时性要求主要体现在快速准确地计算出矢量作用时间以及完成相应的开关控制。
### 3.1.2 SVPWM算法的时间复杂度分析
SVPWM算法的时间复杂度对于实时性至关重要。时间复杂度是一个衡量算法执行时间与输入数据规模之间关系的指标,通常用大O符号表示。对于SVPWM算法,其时间复杂度主要受到以下几个因素影响:
1. 矢量扇区的计算:SVPWM算法需要确定当前矢量所在的扇区,这一过程通常通过比较参考矢量与几个基本矢量的角度或幅值来实现。在最坏情况下,可能需要多次比较才能确定扇区,这部分的时间复杂度通常为O(1),即常数时间复杂度,因为它不随着系统规模的增大而变化。
2. 矢量作用时间的计算:确定扇区后,需要计算出该扇区内三个相邻基本矢量的作用时间。这一过程涉及到的计算较多,例如反三角函数计算、开方、乘除法等。尽管计算过程较为复杂,但在采用优化的数值方法后,这部分的时间复杂度亦可认为是O(1)。
3. PWM波形生成:最后,算法需要基于计算出的作用时间生成PWM波形。这个过程涉及到定时器的配置、中断服务程序的执行等,其时间复杂度取决于硬件平台的能力,通常也能达到O(1)。
综上所述,SVPWM算法整体的时间复杂度能够满足实时系统的要求,关键在于算法的优化和硬件平台的性能。在实际应用中,需要通过软件层面的算法优化和硬件层面的性能提升来共同确保SVPWM算法的实时性能。
## 3.2 硬件资源限制
### 3.2.1 微处理器的计算能力限制
硬件计算能力的限制是实现SVPWM算法的一个重要挑战。在实时系统中,微处理器需要快速响应各种事件并完成复杂的计算任务。对于SVPWM算法而言,这就要求微处理器必须具备高性能的数学计算能力,特别是涉及到浮点运算和三角函数计算的部分。
在设计实时系统时,工程师必须仔细考虑微处理器的性能指标,如主频、指令集、缓存大小等。常用的微处理器包括ARM Cort
0
0





