【提升SVPWM控制精度与效率】：算法优化策略全解析


参考资源链接：[SVPWM原理详解：推导、控制算法及空间电压矢量特性](https://wenku.csdn.net/doc/7g8nyekbbp?spm=1055.2635.3001.10343)
# 1. SVPWM控制技术概述

## 1.1 SVPWM控制技术的起源与发展
SVPWM（Space Vector Pulse Width Modulation）控制技术起源于20世纪70年代，它是一种用于电机驱动和电力转换器的高效调制技术。随着电力电子技术的进步和电机控制需求的提升，SVPWM技术因其高效率、低谐波和良好的动态响应性能，被广泛应用于变频调速、逆变器控制等场景。

## 1.2 SVPWM控制技术的重要性
SVPWM技术的核心优势在于其能够更接近理想的电压矢量调制，从而在交流电机控制中实现更精细的速度和扭矩控制。与传统的正弦波脉宽调制（SPWM）相比，SVPWM在相同开关频率下可以得到更大的输出电压，同时降低电流谐波，提高了电能的利用效率。

## 1.3 SVPWM技术在现代工业的应用
现代工业应用中，SVPWM技术不仅提高了电机驱动系统的性能，还促进了对电机控制策略的创新与优化。其应用领域涵盖了家用电器、电动汽车、风力发电以及工业自动化等众多行业，是现代电力电子技术发展的关键技术之一。

# 2. ```
# 第二章：SVPWM控制的基本原理
## 2.1 SVPWM的数学模型与变换
### 2.1.1 基本数学模型介绍
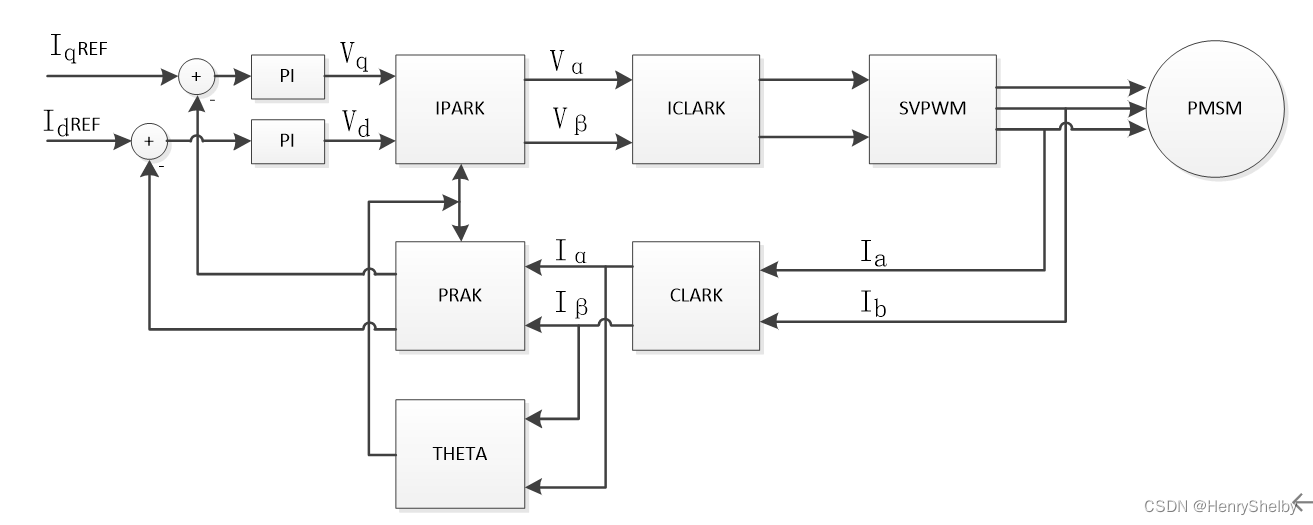
空间矢量脉宽调制（SVPWM）是一种用于三相逆变器的高级调制技术，它通过对逆变器开关状态的精确控制来生成接近圆形的电压矢量轨迹，进而提高电机的输入电压波形质量。其核心在于将电机的三相供电看作是在平面内的矢量，通过合理安排开关状态，使电机两端的电压矢量达到期望的大小和方向。

在SVPWM的基本数学模型中，采用了一种称为正交变换的方法，例如Clark变换和Park变换，将三相静态坐标系下的电压电流矢量转换为两相旋转坐标系下的电压电流矢量。这种转换简化了控制系统的数学描述，并使矢量控制更为直观。

### 2.1.2 变换方法及其影响因素
变换方法的选择对SVPWM控制的性能有直接影响。例如，Clarke变换是将三相变量(x,y,z)转换为两相静止变量(α,β)，公式如下：

\begin{bmatrix}
  x \\
  y \\
  z
\end{bmatrix}
=
\frac{2}{3}
\begin{bmatrix}
  1 & -\frac{1}{2} & -\frac{1}{2} \\
  0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\
  \frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{bmatrix}
\begin{bmatrix}
  \alpha \\
  \beta
\end{bmatrix}

Park变换则是将上述得到的两相静止坐标系下的变量进一步转换为两相旋转坐标系下的变量(d,q)，公式如下：

\begin{bmatrix}
  d \\
  q
\end{bmatrix}
=
\begin{bmatrix}
  \cos{\theta} & \sin{\theta} \\
  -\sin{\theta} & \cos{\theta}
\end{bmatrix}
\begin{bmatrix}
  \alpha \\
  \beta
\end{bmatrix}

其中，θ是旋转坐标系与静止坐标系之间的夹角。

变换方法的选择和实现直接影响SVPWM控制策略的准确性与效率。在实际应用中，变换方法需要结合系统的实时性能和所需的精度来进行选择。

## 2.2 SVPWM的矢量控制策略
### 2.2.1 空间矢量的定义和计算
空间矢量是通过逆变器中六个开关的组合状态来定义的，每个开关状态对应一个空间矢量。在SVPWM中，通过计算和选择合适的开关状态，实现期望的电压矢量输出。空间矢量可以表示为：

\begin{align*}
  V_{k} = V_{dc} \left( \frac{1}{2} e^{j(k-1)\frac{\pi}{3}} \right), \quad k = 1,2,...,6
\end{align*}

其中，V_{dc}是直流侧电压，k代表六个基本空间矢量的位置。

### 2.2.2 控制策略的实施步骤
实施SVPWM控制策略通常包含以下步骤：
1. **计算参考矢量**：根据电机的控制目标计算出电压参考矢量V_{ref}。
2. **扇区判定**：确定V_{ref}所在的扇区，通常通过比较V_{ref}与相邻的V_{1}到V_{6}来实现。
3. **计算作用时间**：基于所选扇区和参考矢量的相对位置，计算各个基本矢量的作用时间。
4. **生成开关序列**：根据作用时间分配每个基本矢量对应的开关状态，产生脉宽调制波形。

开关序列的生成是SVPWM控制中的关键，它直接影响到逆变器输出电压的质量和电机的运行性能。

## 2.3 SVPWM的调制过程分析
### 2.3.1 开关序列的生成方法
开关序列的生成方法通常是基于离散化原理，通过计算得到一系列开关动作指令，从而构造逆变器的开关序列。生成开关序列的方法有多种，但核心在于将期望的输出电压矢量在空间上进行细分，分配给不同的开关状态，以此控制逆变器输出。

### 2.3.2 调制过程中的波形分析
在调制过程中，通过对开关序列的时序控制，可以得到逆变器输出的电压波形。对于SVPWM来说，其目标是使输出电压波形接近理想的圆形轨迹，以减小谐波含量并提升电机效率。

调制过程中的波形分析通常需要依据实时反馈的信息，对开关序列进行动态调整。在实际应用中，通常会涉及到复杂的计算，以保证控制的精度和实时性。

以上内容仅为第二章的部分详细章节内容。每个章节内容需要达到既定的字数要求，包含代码块、表格、列表、mermaid流程图等元素，并对代码、mermaid流程图、表格进行必要的说明。确保章节内容的逻辑性和连贯性，使得文章内容对IT行业和相关行业从业者都有深入的吸引力和教育意义。

# 3. SVPWM算法的常见问题与挑战

在电气驱动系统中，空间矢量脉宽调制（SVPWM）因其优异的性能而被广泛应用于电机控制。然而，这一算法在实际应用中也面临一系列挑战，包括控制精度不足、效率低下以及硬件平台限制等问题。本章将深入探讨这些挑战，并分析其原因与潜在的解决方案。

## 3.1 算法精度不足的原因分析

### 3.1.1 精度损失的主要因素

在SVPWM算法中，精度的损失可能来源于多个方面，主要包括以下几个主要因素：

- **数值计算误差**：在进行空间矢量的计算时，由于浮点数的舍入误差，导致最终的结果与理论值存在偏差。在某些情况下，这些小的误差会累积，从而影响到调制波的精度。
- **离散时间处理**：SVPWM是一种基于数字控制的技术，需要在离散时间点上采样和处理信号。这种离散化处理可能导致波形的失真，进而影响调制精度。
- **测量噪声和干扰**：实际应用中的测量噪声和电磁干扰可能会引入误差，尤其是在电机高速运行时，这些噪声和干扰的影响更加显著。

### 3.1.2 精度提升的现有方法

为了提升SVPWM