电力潮流计算的直角坐标方法：从理论到实践的完整流程


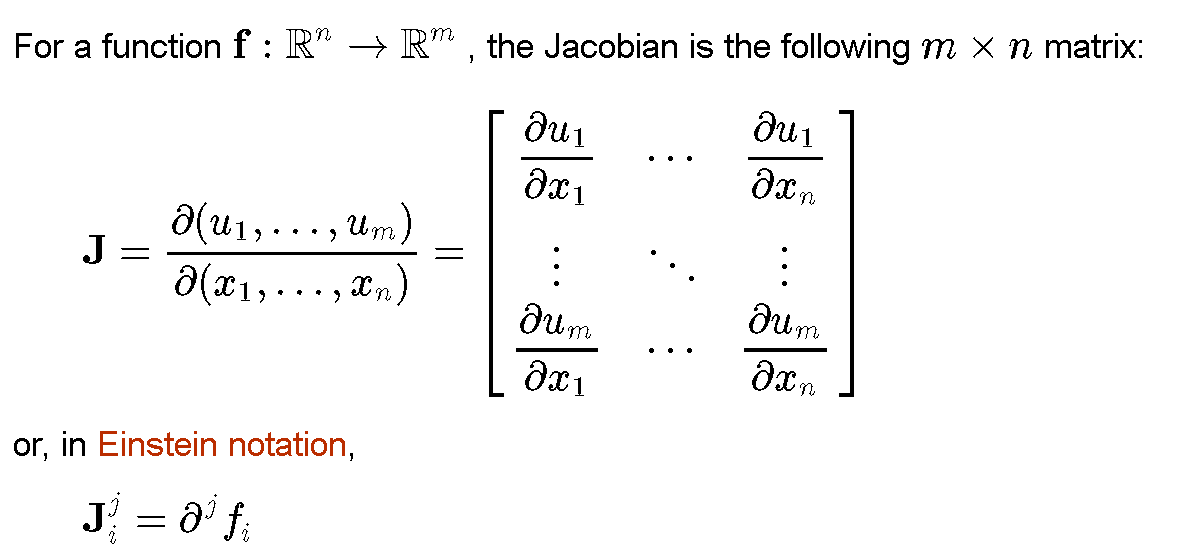
# 摘要
电力潮流计算是电力系统分析中的核心任务，对于电力系统的规划、运行和管理具有重要意义。本文首先概述了电力潮流计算的基本理论和直角坐标方法的原理，包括坐标系统的定义、电力系统模型的建立以及节点导纳矩阵的构建。接着，详细解读了直角坐标方法在潮流计算中的应用，从计算步骤到模拟分析，以及误差来源和校正方法。文章还讨论了潮流计算软件的使用、实际案例演练和结果的解读应用。最后，探讨了大数据和人工智能技术结合下的潮流计算前沿问题，以及可再生能源并网和电力系统智能化对潮流计算带来的挑战和未来发展。

# 关键字
电力潮流计算；直角坐标方法；节点导纳矩阵；误差分析；软件选择；前沿技术

参考资源链接：[电力系统潮流计算：节点电压与功率方程解析](https://wenku.csdn.net/doc/3taowbqr1b?spm=1055.2635.3001.10343)
# 1. 电力潮流计算概述

## 1.1 电力潮流计算的重要性
电力潮流计算是电力系统分析的核心内容之一，它旨在确定在给定负荷条件下，电力网络中各线路和变压器的功率流动情况和节点电压的大小与相位。这些信息对电力系统的稳定运行、规划、设计和管理至关重要。正确的潮流计算结果能够帮助工程师进行有效的电力网络优化，减少损耗，提升系统效率，同时还能预防潜在的过载和故障问题。

## 1.2 潮流计算的发展历程
潮流计算的历史可以追溯到20世纪初，早期的方法主要是基于手工计算，随着计算机技术的发展，潮流计算由手工计算逐渐转向计算机辅助分析。从最初的直流潮流计算方法，发展到如今更为精确的交流潮流计算方法，其中包括了直角坐标方法、极坐标方法和各种迭代算法等。潮流计算的演进为电力系统的分析提供了更加丰富的工具和方法，也使得电力系统的规划与运行变得更加科学和高效。

## 1.3 潮流计算与现代电力系统
在现代电力系统中，随着可再生能源的大量并网和电力电子设备的广泛使用，传统的潮流计算方法面临着新的挑战。潮流计算必须适应这些变化，以确保电力系统能够稳定、高效地运行。此外，新的技术如大数据分析、人工智能和机器学习的应用，为潮流计算带来了新的可能性，可以处理更加复杂的网络和实时计算的需求。在本章中，我们将概述电力潮流计算的基本概念和重要性，为后续章节更深入的讨论打下基础。

# 2. 直角坐标方法的理论基础

### 2.1 直角坐标系统的定义和特性

#### 2.1.1 坐标系统的数学定义
直角坐标系统是由一对垂直的坐标轴构成的，通常被称为x轴和y轴。在平面上任意一点的位置可以通过一对实数（x, y）来表示，这个点就位于以原点为起点，到该点水平距离为x，垂直距离为y的位置。数学上，这个点P可以表示为P(x, y)。在此系统中，所有的点都可以用两个数值来精确确定。

#### 2.1.2 直角坐标与电力系统的关系
在电力系统中，直角坐标系统被广泛应用于潮流计算和网络分析中。因为电力系统的各个节点、输电线和负载通常都具有特定的物理位置，使用直角坐标能够直观地将这些组件映射到二维平面上，方便进行空间位置的分析和计算。此外，由于直角坐标系统符合欧几里得几何的规则，所以可以应用许多成熟的数学工具和方法进行复杂的电气量计算，比如使用节点导纳矩阵在直角坐标系下进行电力潮流计算。

### 2.2 电力潮流计算的基本原理

#### 2.2.1 潮流计算的目标和意义
潮流计算（Load Flow Analysis）是电力系统分析中的核心，主要目标是确定系统在特定负荷条件下的电压分布、线路流过的电流大小以及功率分布。进行潮流计算的意义在于，它可以帮助设计和规划电网、提高电力系统的运行效率、保障电网的安全稳定运行、辅助进行故障分析与预防，以及优化系统经济性。

#### 2.2.2 潮流计算中的基本假设和约束条件
为了简化计算过程，潮流计算通常基于以下几个基本假设：
1. 电力系统是一个稳定的交流系统，频率固定。
2. 负载是恒定的，即负荷不随时间变化。
3. 系统中的所有线路和设备均为理想无损元件，忽略电阻损耗。
4. 电力系统中的发电机输出电压和相位角可控，且保持恒定。
基于这些假设，潮流计算需要解决的问题就是在这些约束条件下，通过计算来确定系统中各节点的电压大小和相位角，以及各支路的功率流动。

### 2.3 直角坐标方法的工作流程

#### 2.3.1 系统建模与参数设定
系统建模是进行潮流计算的第一步，它涉及到将实际电力系统的物理结构转换成数学模型。在直角坐标系统中，这包括定义节点的位置、线路的连接关系、线路的阻抗参数、发电机和负载的参数等。建模过程需要将每个组件的位置转换为直角坐标（x, y），并为每条线路和设备赋予相应的阻抗值。

#### 2.3.2 节点导纳矩阵的构建与应用
节点导纳矩阵是潮流计算的核心工具之一，它是一个表示节点间电气联系的矩阵，其中包含了线路的电导和电纳信息。构建节点导纳矩阵首先要确定系统的节点数量，然后根据系统模型中的线路连接情况，计算出各个节点之间的电纳值。导纳矩阵的每一项代表了系统中某两个节点之间的电纳联系。

使用节点导纳矩阵，可以将电力系统的电路方程表示为YV=I的形式，其中Y是节点导纳矩阵，V是节点电压向量，I是节点电流向量。通过求解这个方程组，可以得到电力系统的潮流分布。

import numpy as np

# 假设系统有3个节点，构建节点导纳矩阵Y
Y = np.array([[0.1+0.01j, -0.01j, 0],
              [-0.01j, 0.1+0.01j, -0.01j],
              [0, -0.01j, 0.1+0.01j]])

# 假设节点电压向量V
V = np.array([1.0, 1.0, 1.0])

# 计算节点电流向量I
I = np.dot(Y, V)

print("节点电流向量I:", I)

在上述代码块中，我们创建了一个3x3的节点导纳矩阵，并假设了一个简单的节点电压向量。通过矩阵乘法，我们得到了节点电流向量I。在实际应用中，节点数量将远大于3，节点导纳矩阵将更加复杂，并且需要解耦合技术来处理。

# 3. 直角坐标方法在潮流计算中的应用

在电力系统分析中，潮流计算占据着核心位置，而直角坐标方法作为一种常用的计算技术，在确保计算精度与效率方面发挥着重要作用。本章将详细解读直角坐标方法在潮流计算中的应用，通过案例研究和模拟分析，深入探讨其在实际操作中的步骤和优化。

## 3.1 计算步骤的详细解读

直角坐标方法的应用是电力潮流计算领域的一项基础且重要的技术。为了更好地理解其操作流程，我们将其计算步骤分为初始条件的设定和高