混合加权定位技术：精度提升与实验验证的全面解析


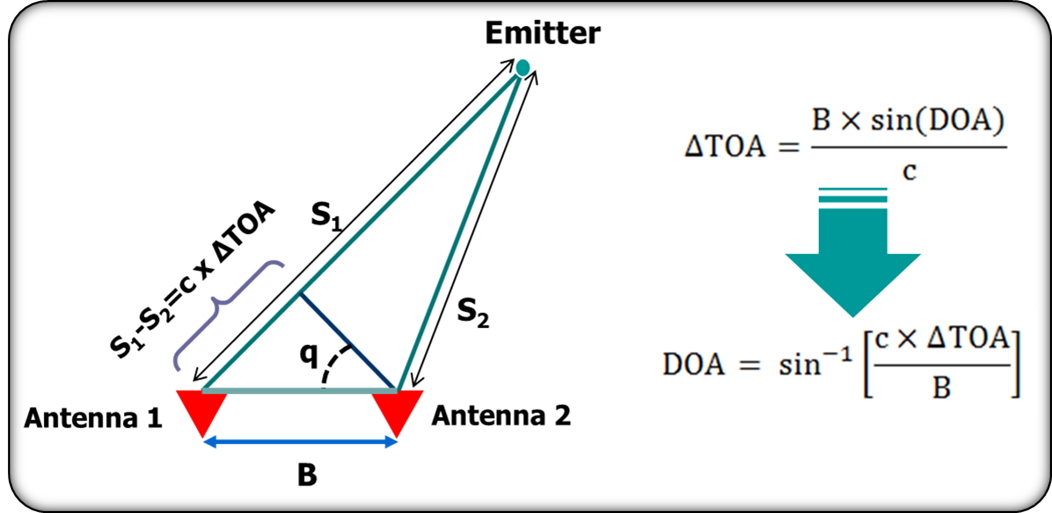
参考资源链接：[MATLAB实现Chan-Taylor混合加权算法进行TDOA定位](https://wenku.csdn.net/doc/aibjxu0sw0?spm=1055.2635.3001.10343)
# 1. 混合加权定位技术概述

在本章中，我们将介绍混合加权定位技术的基本概念及其重要性。我们将探讨该技术如何应用于多个领域，并简要说明其在当前技术环境中的地位和作用。

## 1.1 混合加权定位技术简介

混合加权定位技术是一种将多种定位方法和数据源相结合的技术，旨在提高定位的精确性和可靠性。这种技术考虑到不同的信号源（如GPS、Wi-Fi、蓝牙等）具有不同的优势和限制，并利用算法对不同信号源的数据进行加权计算，以得到更为准确的位置信息。

## 1.2 技术背景与发展

近年来，随着物联网(IoT)和智能设备的普及，对高精度定位的需求不断增长。传统的单一信号源定位方法已不能满足复杂的现实需求，因此混合加权定位技术应运而生，成为解决定位精度问题的重要手段。

## 1.3 应用领域

混合加权定位技术的应用领域广泛，包括但不限于智能交通系统、室内导航、资产追踪、紧急救援、农业和自然资源管理。该技术的应用极大地提升了这些领域服务的准确性和效率。

在接下来的章节中，我们将深入探讨混合加权定位技术的理论基础、关键实现步骤、以及在实际应用中的案例研究。

# 2. 基础理论与算法架构

## 2.1 定位技术的理论基础

### 2.1.1 定位系统的工作原理

定位系统的核心在于捕捉到的信号与已知位置的信标（beacons）或基站（base stations）之间的相对关系。在这一过程中，设备（例如智能手机或车载GPS）利用接收的信号强度、到达时间和角度等信息来推断自身的位置。定位系统的实现可以分为以下三个基本步骤：

1. **信号发射**：信号源（如GPS卫星）发射具有特定特征的信号。
2. **信号接收与测量**：定位设备接收信号并测量信号的某些属性，如时间延迟、信号强度等。
3. **位置计算**：根据测量到的信号属性和信号源位置，采用特定的算法计算出设备的位置坐标。

### 2.1.2 信号传播和误差分析

信号在传播过程中会受到多种因素的影响，这包括但不限于大气条件、建筑物反射或阻挡、多径效应等，导致信号发生衰减、扩散、延迟或相位变化，最终影响定位精度。例如：

- **大气延迟**：信号通过电离层和对流层时，其传播速度会减慢，导致到达时间的误差。
- **多径效应**：信号反射和折射产生的多个路径到达接收器，会引起信号强度和时间的不稳定，导致定位误差。
- **设备误差**：定位设备的内部时钟偏差、测量噪声等，也会引入误差。

为了减少这些误差，现代定位系统采用了多种技术，如差分GPS（DGPS）和实时动态定位（RTK）等。

## 2.2 混合加权定位算法原理

### 2.2.1 加权算法的基本概念

加权算法通过赋予不同信号源或定位参数不同的权重来提高定位精度。这些权重基于信号质量、误差模型以及信号源的可靠性来确定。权重的确定通常通过以下公式实现：

\[ x = \frac{\sum_{i=1}^{n} w_i \cdot x_i}{\sum_{i=1}^{n} w_i} \]

这里，\( x \) 表示最终的定位结果，\( w_i \) 表示第 \( i \) 个信号源的权重，\( x_i \) 表示基于该信号源的定位估计值，而 \( n \) 是信号源的总数。

### 2.2.2 混合加权方法的优势

混合加权方法结合了多种定位技术的优点，例如GPS、Wi-Fi、蓝牙、IMU（惯性测量单元）等，通过最优化权重分配，在不同的环境和条件下保持定位的高准确性和鲁棒性。混合方法的优势在于：

- **更高的定位精度**：在理想条件下，可以达到更高的定位精度。
- **更好的环境适应性**：混合方法能够在不同的环境中自动调整，如在室内采用Wi-Fi定位，在户外使用GPS。
- **更强的容错能力**：当某一种信号源不可用或信号质量差时，可以依赖其他信号源继续工作。

## 2.3 算法数学模型构建

### 2.3.1 坐标系统的选择和转换

在构建定位算法的数学模型时，需要先选择合适的坐标系统。常用的选择有地理坐标系统（经纬度）和笛卡尔坐标系统。由于多数定位计算在数学上更易于使用笛卡尔坐标，因此在实际应用中通常需要将经纬度坐标转换为笛卡尔坐标。

转换过程可以通过以下数学公式实现：

\[ X = (N + h) \cdot \cos(\phi) \cdot \cos(\lambda) \]
\[ Y = (N + h) \cdot \cos(\phi) \cdot \sin(\lambda) \]
\[ Z = \left[(N \cdot (1 - e^2)) + h\right] \cdot \sin(\phi) \]

其中，\(X, Y, Z\) 是笛卡尔坐标系下的点，\(N\) 是卯酉圈曲率半径，\(h\) 是大地高度，\(\phi\) 是地理纬度，\(\lambda\) 是地理经度，\(e\) 是椭球体的第一偏心率。

### 2.3.2 误差模型和方程的建立

为了准确计算位置，需要建立误差模型来纠正信号传播和设备读数中的误差。误差模型通常包括系统误差和随机误差，模型的构建需要依据具体的定位场景进行调整。一个常见的误差模型方程如下：

\[ \Delta s = s_0 + \Delta s_{sys} + \Delta s_{ran} \]

在该方程中：

- \(\Delta s\) 表示总的信号误差。
- \(s_0\) 表示信号的理想传播时间或强度。
- \(\Delta s_{sys}\) 表示系统误差，比如设备时钟偏差。
- \(\Delta s_{ran}\) 表示随机误差，如多径效应。

通过收集足够的数据并使用统计分析方法，可以估计并修正上述误差模型中的系统误差和随机误差部分。在实际应用中，还需要考虑如多普勒效应、天线相位中心偏移等因素，并通过动态校正算法进行实时误差校正。

以上阐述了混合加权定位技术中基础理论与算法架构的主要内容，包括了定位技术的理论基础、加权算法的原理以及算法数学模型构建的细节。在接下来的章节中，我们将会深入探讨混合加权定位技术的关键技术和实践操作。

# 3. 关键技术和实践操作

混合加权定位技术的关键在于将不同来源的数据进行有效整合，以达到高精度定位的目的。这一章节将深入探讨数据采集与处理的策略，混合加权定位的实施步骤，以及如何对定位精度进行评估。

## 3.1 数据采集与处理

### 3.1.1 传感器的选择和部署

定位系统的精度在很大程度上取决于所选用的传感器。不同类型的传感器具有不同的测量精度、成本和应用场景。因此，针对特定的定位需求，选择恰当的传感器是至关重要的。

例如，全球导航卫星系统（GNSS）的信号可用于室外宽区域定位；惯性测量单元（IMU）能够提供短期的高精度移动速度和方向信息；而超宽带（UWB）技术则适合高精度室内定位。

在部署传感器时，应考虑以下因素：
- 环境适应性：传感器是否能在预期的环境条件下稳定工作。
- 成本效益：选择性价比高的传感器，以保证项目的经济性。
- 互操作性：确保不同传感器间的兼容性和数据同步。

### 3.1.2 数据预处理和噪声去除

采集到的原始数据往往包含了大量噪声和不准确的测量值。在进行加权处理之前，必须对数据进行预处理，以提高其质量。