【大型项目中JS树结构转换】：挑战应对与策略优化

# 1. JavaScript树结构转换概述

在当今的IT行业中，树结构作为数据存储和操作的重要方式，在各种应用中无处不在，尤其在前端工程化、数据可视化等场景中扮演着关键角色。JavaScript，作为一种广泛使用的编程语言，对树结构的操作和转换提供了强大的支持。在这一章节中，我们将概述树结构的基本概念，分析其在JavaScript中的转换需求，并探讨其应用意义，为后续章节的深入探讨打下坚实的基础。我们将从树结构的定义开始，逐步深入到其转换的需求分析，以及为什么JavaScript是处理树结构转换的理想工具。

# 2. 树结构的基础理论与应用

## 2.1 树结构的定义和分类

### 2.1.1 树结构的基本概念

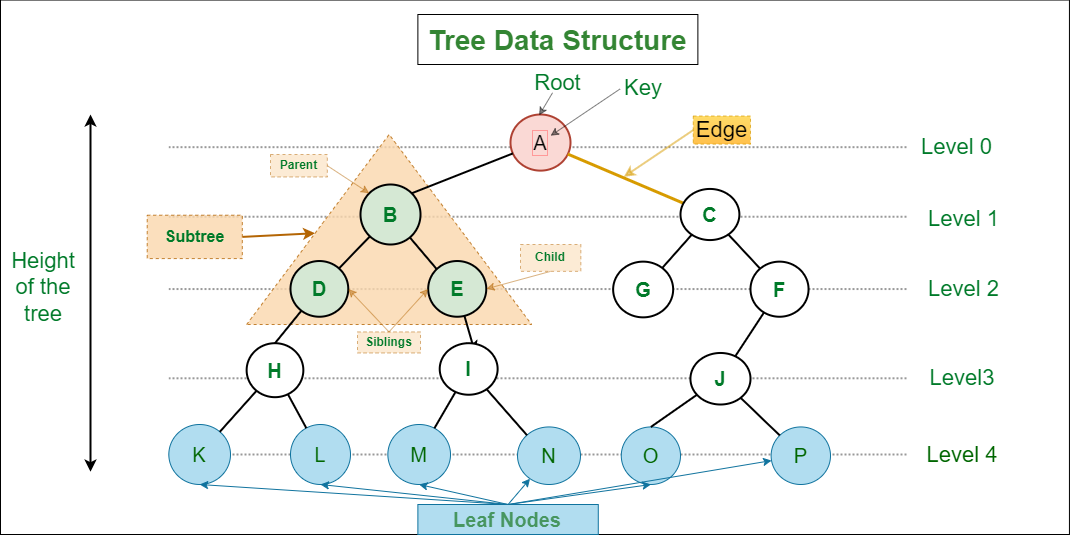
在计算机科学中，树结构是一种非线性数据结构，用于模拟具有层次关系的数据。它是由节点（Node）和连接节点的边（Edge）组成的集合。树结构用于表示具有层级关系的数据，其中每个节点都可以有零个或多个子节点，而根节点是整个结构的起始节点，没有父节点。

树结构的几个重要术语包括：

- **根节点（Root）**：树的顶部节点，没有父节点。
- **子节点（Child）**：一个节点直接连接的节点。
- **父节点（Parent）**：任何节点直接连接的上一个节点。
- **叶节点（Leaf）**：没有子节点的节点。
- **子树（Subtree）**：节点及其后代构成的树。

### 2.1.2 常见树结构的种类和特性

不同种类的树结构有其特定的应用场景和特性：

- **二叉树（Binary Tree）**：每个节点最多有两个子节点，通常用于高效的查找和排序算法。
- **二叉搜索树（Binary Search Tree, BST）**：是一种特殊的二叉树，其中左子树的所有值都小于其父节点，右子树的所有值都大于其父节点，常用于数据查找。
- **平衡树（Balanced Tree）**：一种通过旋转来维持高度平衡的树，如AVL树和红黑树，用于优化二叉搜索树的性能，使操作保持在对数时间复杂度。
- **堆（Heap）**：一种特殊的完全二叉树，所有父节点的值都大于或等于其子节点的值（最大堆），用于实现优先队列等。
- **B树（B-Tree）/B+树（B+Tree）**：多路平衡查找树，广泛用于数据库和文件系统的索引，可以存储大量数据且磁盘读写效率高。

## 2.2 树结构在大型项目中的角色

### 2.2.1 数据组织与管理中的树结构

在大型项目中，树结构常用于数据的组织和管理，为复杂的数据关系提供清晰的层次。例如，文件系统的目录结构、UI组件的层级关系、权限控制的组织等，都可通过树结构清晰地展现出来。

- **文件系统的目录结构**：树状结构非常适合表示文件和目录之间的层次关系，每个目录可以包含多个文件和子目录，形成清晰的层级。
- **UI组件的层级关系**：在前端开发中，组件的父子关系、嵌套关系经常使用树结构来表示，从而实现组件的复用和状态管理。
- **权限控制的组织**：企业中的组织架构、角色和权限的分配往往也可以通过树状结构来进行清晰的划分和管理。

### 2.2.2 树结构在前端框架中的应用

前端框架中广泛运用了树结构来处理组件的渲染和状态管理，例如：

- **React的虚拟DOM**：React使用虚拟DOM树结构来记录和比较实际DOM状态，从而高效地更新视图。
- **Redux中的状态树**：Redux使用树结构来组织全局状态，组件可以很方便地访问和更新状态树的特定部分。
- **Vue的组件树**：Vue框架中，组件之间的父子关系构成了一个组件树，帮助开发者管理组件的生命周期和数据流动。

## 2.3 树结构转换的需求分析

### 2.3.1 转换的场景和目的

在实际应用中，可能遇到需要将数据从一种树状结构转换为另一种结构的场景，这可能由以下需求驱动：

- **数据展示**：将扁平化的数据转换成层次化的树状结构，以便以更直观的方式展示。
- **性能优化**：通过转换结构来减少不必要的DOM操作，提高渲染效率。
- **功能实现**：实现如拖拽排序、权限管理等特定功能，需要对节点关系进行重新组织。
- **跨平台兼容**：在不同平台或系统间迁移数据时，需要进行结构转换以适配新的格式。

### 2.3.2 转换前的准备工作

在开始转换之前，需要做好以下准备工作：

- **分析源数据结构**：了解源数据的格式、属性和关系，这是制定转换策略的基础。
- **确定目标结构**：明确转换后的树状结构需要满足的要求和特性，以指导转换过程。
- **考虑转换逻辑**：根据源结构和目标结构制定转换算法，包括节点的匹配、插入和删除规则。
- **测试案例准备**：准备一些典型的转换案例，以便在转换完成后进行测试验证。

接下来，我们将深入探讨JavaScript中的树结构操作实践，以及如何在大型项目中策略性地应用树结构转换。

# 3. JavaScript中的树结构操作实践

## 3.1 JavaScript树节点的创建与遍历

### 3.1.1 节点的创建方法和属性定义

在JavaScript中创建树结构的节点通常需要定义一个基础的构造函数或类，来包含节点的基本信息，比如标识符、父节点引用、子节点列表等。下面是一个简单的节点构造函数示例：

function TreeNode(data) {
  this.id = data.id;
  this.parent = null;
  this.children = [];
  this.data = data;
}

在这个构造函数中，`id` 是节点的唯一标识，`parent` 是一个引用，指向当前节点的父节点，而 `children` 是一个数组，包含当前节点的所有子节点。`data` 属性可以存储任何与节点相关的数据。

创建节点实例后，我们可以通过修改 `parent` 和 `children` 属性来构建整个树结构。以下是如何创建并初始化树结构的示例：

const rootData = { id: 0 };
const root = new TreeNode(rootData);

const child1Data = { id: 1 };
const child1 = new TreeNode(child1Data);
root.children.push(child1);
child1.parent = root;

const child2Data = { id: 2 };
const child2 = new TreeNode(child2Data);
root.children.push(child2);
child2.parent = root;

这个例子中，我们创建了一个根节点 `root` 和两个子节点 `child1` 和 `child2`，然后将子节点加入到根节点的 `children` 数组中，并设置它们的 `parent` 属性。

### 3.1.2 深度优先与广度优先遍历算法

遍历树结构是许多树操作的基础，包括深度优先（DFS）和广度优先（BFS）两种常见的算法。

深度优先遍历通过递归的方式遍历每个节点，通常会访问到树的最底层节点，然后再回溯。以下是一个深度优先遍历的示例：

function dfsVisit(node) {
  console.log(node.data); // 处理当前节点
  node.children.forEach(dfsVisit); // 递归处理每个子节点
}

dfsVisit(root); // 从根节点开始遍历

广度优先遍历则是使用队列来进行层次遍历。我们首先访问根节点，然后访问根节点的所有子节点，再访问这些子节点的子节点，以此类推。以下是广度优先遍历的示例：

function bfsVisit(node) {
  let queue = [node]; // 使用数组作为队列来存储待访问节点

  while (queue.length) {
    let currentNode = queue.shift(); // 弹出第一个元素
    console.log(currentNode.data); // 处理当前节点
    queue.push(...currentNode.children); // 将所有子节点加入队列
  }
}

bfsVisit(root); // 从根节点开始遍历

## 3.2 树结构的增删改查操作

### 3.2.1 添加节点

添加节点通常意味着在特定节点下添加一个或多个子节点。首先创建新的节点实例，然后将其加入到父节点的 `children` 数组中，并设置新节点的 `parent` 属性。

function addChild(parentNode, childData) {
  const childNode = new TreeNode(childData);
  parentNode.children.push(childNode);
  childNode.parent = parentNode;
}

// 假设已有一个树结构和节点
 addChild(child1, { id: 3 }); // 在child1下添加一个新的子节点

### 3.2.2 删除节点

删除节点稍微复杂，需要先从父节点的 `children` 数组中移除指定的节点，然后将该节点的所有子节点都提升一级，变成父节点的直接子节点。

function removeNode(nodeToRemove) {
  if (nodeToRemove.parent) {
    const index = nodeToRemove.parent.children.indexOf(nodeToRemove);
    nodeToRemove.parent.children.splice(index, 1); // 从父节点中移除

    // 将子节点提升一级
    nodeToRemove.children.forEach(child => {
      child.parent = nodeToRemove.parent;
      nodeToRemove.parent.children.push(child);
    });
    nodeToRemove.children.length = 0; // 清空原节点的子节点数组
  }
}

removeNode(child2); // 删除child2节点及其子树

### 3.2.3 修改节点数据

修改节点数据很