【数字逻辑与计算机架构】：《Digital Fundamentals》第11版对计算机科学的深远影响


参考资源链接：[托马斯·弗洛伊德第11版《数字基础》全球版：经典电子技术教程](https://wenku.csdn.net/doc/13rz298e43?spm=1055.2635.3001.10343)
# 1. 数字逻辑基础及其在计算机架构中的作用

数字逻辑是计算机科学和电子工程的基石。理解数字逻辑的重要性首先源于其构建基础——逻辑门电路。逻辑门通过基本的逻辑运算（如AND、OR、NOT）组合起来，构成了更复杂的逻辑电路。这些电路是实现各种数字功能，如算术运算和数据传输的基础。

组合逻辑和时序逻辑是数字逻辑的两个核心概念。组合逻辑的输出仅依赖于当前输入，而时序逻辑则依赖于时间，其输出也依赖于先前状态。这种区分对于理解计算机内部的时钟同步、内存和状态机设计至关重要。

在计算机架构中，数字逻辑被用于设计CPU、存储器和输入/输出系统。CPU中的算术逻辑单元（ALU）就体现了数字逻辑的应用，而存储器的编址、指令的解码等也都建立在这些原理之上。掌握数字逻辑不仅有助于理解计算机的运作方式，还对于硬件编程和系统优化有着不可或缺的作用。接下来的章节将深入探讨这些关键概念如何影响现代计算机架构的设计和发展。

# 2.1 数字电路基础
数字电路是构成现代电子系统的基础。其核心在于使用逻辑门构建各种逻辑电路，实现复杂的逻辑功能。其中，逻辑门是数字电路的基本构建单元，它们根据输入电平的不同，输出特定的电平状态。

### 2.1.1 逻辑门和逻辑电路

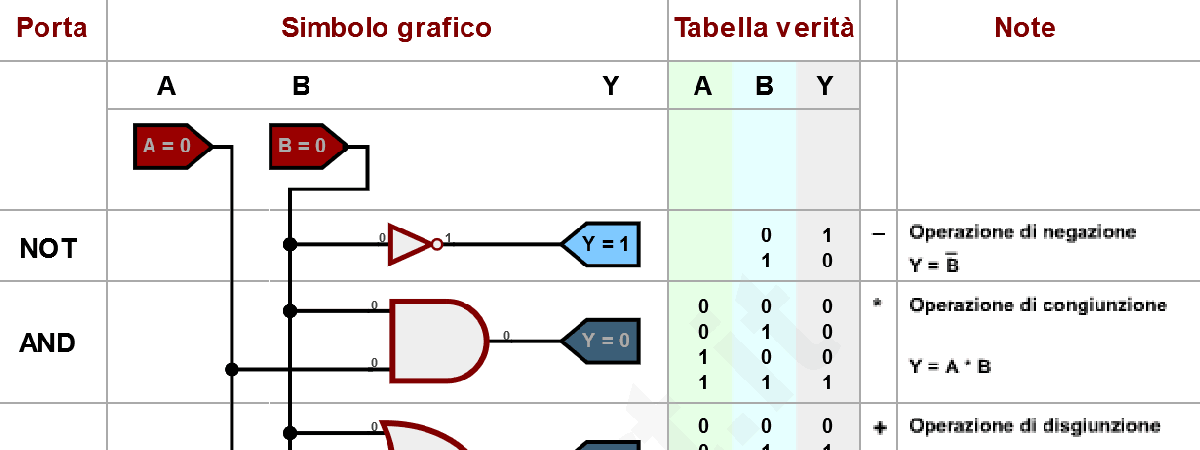
逻辑门是一种物理设备，它按照预定义的逻辑运算规则进行工作，例如AND、OR、NOT、NAND、NOR、XOR等门。在数字电路中，这些基本逻辑门被组合使用以构建更为复杂的电路。

举个例子，当两个输入同时为高电平时，AND门的输出才为高电平；而OR门只要任一输入为高电平，输出即为高电平。NOT门是一个单输入的门，它将输入信号取反，即高电平输入产生低电平输出，反之亦然。

graph TD
    A[输入A] -->|AND| C[AND门]
    B[输入B] -->|AND| C
    C --> D[输出]

    E[输入X] -->|OR| G[OR门]
    F[输入Y] -->|OR| G
    G --> H[输出]

    I[输入Z] -->|NOT| J[NOT门]
    J --> K[输出]

逻辑电路是由逻辑门组合形成的电路，它可以执行更复杂的逻辑操作。比如，一个简单的组合逻辑电路可以是一个4位加法器，它使用多个全加器（Full Adder）逻辑门来实现。

### 2.1.2 组合逻辑和时序逻辑

数字电路分为组合逻辑和时序逻辑两大类。

- **组合逻辑**电路的输出仅取决于当前的输入值，不包含任何记忆元素。常见的组合逻辑电路包括解码器、编码器、多路复用器、加法器等。
- **时序逻辑**电路除了输入信号外，还包含内部存储元件（如触发器或锁存器），这些存储元件的状态决定电路的输出。时序逻辑电路能够根据输入信号以及电路过去的状态产生输出，因此它们常用于设计计数器、寄存器和存储器。

## 2.2 数制和代码

在数字电子中，信息以二进制形式表示。二进制是计算机内部工作语言，但计算机与其他系统交互时，还会用到八进制和十六进制数制。

### 2.2.1 二进制、八进制和十六进制数制

- **二进制**系统是最基本的数字系统，只使用两个数字0和1。
- **八进制**系统每三位二进制数对应一个八进制数位，优点是简明且易于转换。
- **十六进制**系统每四位二进制数对应一个十六进制数位，由于计算机中以字节（8位）为单位存储数据，十六进制可以更方便地表示一个字节。

graph TD
    A[二进制] -->|3位对应1位| B[八进制]
    A -->|4位对应1位| C[十六进制]

### 2.2.2 错误检测与校正码

在数据传输和存储过程中，为了检测和纠正可能出现的错误，数字系统广泛使用错误检测与校正码。常见的包括奇偶校验位、循环冗余检验（CRC）以及海明码等。这些方法为数字系统提供了数据的完整性和可靠性保障。

graph LR
    A[原始数据] -->|添加校验位| B[带奇偶校验位的数据]
    B -->|传输| C[接收方]
    C -->|检查校验位| D[错误检测]
    D -->|有错| E[请求重发]
    D -->|无错| F[接受数据]

## 2.3 数据表示和处理

数字系统必须能够有效地表示和处理数据。数据可以是数字、文本、图像等多种形式，每种形式都有其特定的表示方法和处理要求。

### 2.3.1 数据表示方法

数据在计算机中以数字形式表示，最常见的有定点数和浮点数两种表示方法。定点数适用于表示整数，而浮点数则用于表示小数。

浮点数表示方法借鉴了科学记数法的概念，它将数值表示为一个基数和一个指数的乘积，其中基数部分称为尾数，指数部分决定了小数点的位置。IEEE 754是目前广泛使用的浮点数标准，它规定了数据格式、舍入规则以及操作细节。

### 2.3.2 加法器和乘法器设计

为了处理数据，数字系统需要执行算术运算。加法器和乘法器是数字电路中执行基础算术运算的关键组成部分。

加法器将两个或多个二进制数相加，生成结果和可能的进位。最基本的加法器是半加器，它可以处理两个一位二进制数的相加，但不考虑进位。全加器在半加器的基础上增加了一个进位输入，因此可以处理三个一位二进制数的相加。

乘法器执行的是两个二进制数的乘法运算，其设计比加法器复杂。最常见的乘法器设计方法有移位相加法、Booth算法和W