深入理解MATLAB数值计算：揭开数值计算的奥秘

# 1. MATLAB数值计算基础

MATLAB是一种用于数值计算和数据分析的高级编程语言。它提供了广泛的内置函数和工具箱，使数值计算变得简单高效。本章将介绍MATLAB数值计算的基础知识，包括：

- **数值表示：**了解MATLAB中数字的表示方式，包括浮点表示和精度。
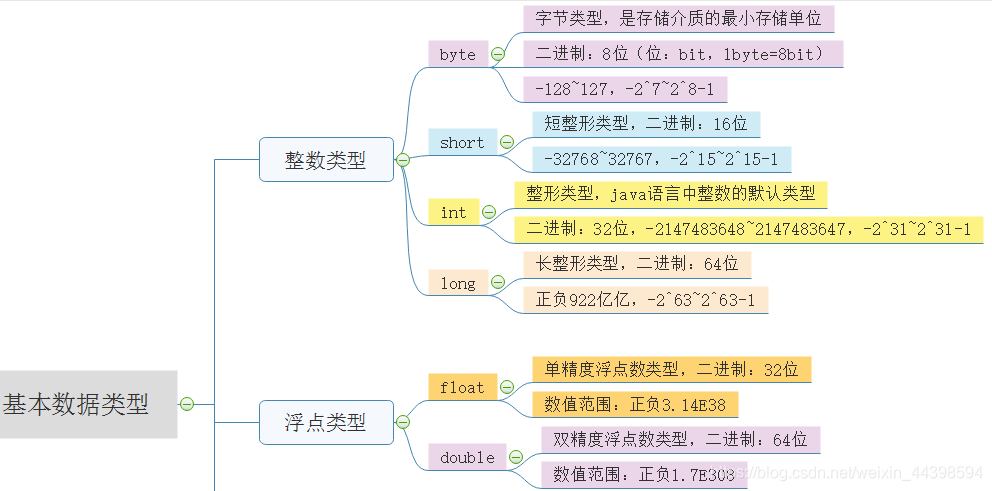
- **数据类型：**熟悉MATLAB中不同的数据类型，例如整数、实数、复数和字符数组。
- **算术运算：**掌握MATLAB中基本的算术运算，包括加、减、乘、除和幂运算。
- **矩阵和数组操作：**学习如何创建、操作和管理MATLAB中的矩阵和数组，包括矩阵乘法、转置和元素运算。

# 2. MATLAB数值计算技术

### 2.1 数值积分和微分

#### 2.1.1 数值积分方法

**梯形法则**

梯形法则是一种数值积分方法，它将积分区间等分成若干个子区间，并用每个子区间的梯形面积来近似积分值。其公式为：

∫[a, b] f(x) dx ≈ (b - a) / 2 * [f(a) + f(b)]

**辛普森法则**

辛普森法则是一种比梯形法则更精确的数值积分方法，它将积分区间等分成偶数个子区间，并用每个子区间的抛物线面积来近似积分值。其公式为：

∫[a, b] f(x) dx ≈ (b - a) / 6 * [f(a) + 4f((a + b) / 2) + f(b)]

#### 2.1.2 数值微分方法

**向前差分**

向前差分是一种数值微分方法，它使用函数在当前点和前一个点的值来近似导数值。其公式为：

f'(x) ≈ (f(x + h) - f(x)) / h

**中心差分**

中心差分是一种比向前差分更精确的数值微分方法，它使用函数在当前点和前后一个点的值来近似导数值。其公式为：

f'(x) ≈ (f(x + h) - f(x - h)) / (2h)

### 2.2 线性方程组求解

#### 2.2.1 直接求解法

**高斯消去法**

高斯消去法是一种直接求解线性方程组的方法，它通过一系列行变换将系数矩阵化为上三角矩阵，然后从上到下逐个求解未知数。

#### 2.2.2 迭代求解法

**雅可比迭代法**

雅可比迭代法是一种迭代求解线性方程组的方法，它通过反复更新未知数的值来逼近解。其公式为：

x_i^(k+1) = (b_i - ∑_{j=1, j≠i}^n a_{ij}x_j^(k)) / a_{ii}

**高斯-赛德尔迭代法**

高斯-赛德尔迭代法是一种比雅可比迭代法更快的迭代求解线性方程组的方法，它在更新未知数时使用最新的值。其公式为：

x_i^(k+1) = (b_i - ∑_{j=1}^{i-1} a_{ij}x_j^(k+1) - ∑_{j=i+1}^n a_{ij}x_j^(k)) / a_{ii}

### 2.3 非线性方程组求解

#### 2.3.1 一元非线性方程求解法

**牛顿-拉夫森法**

牛顿-拉夫森法是一种一元非线性方程求解方法，它使用函数的导数来迭代更新近似解。其公式为：

x^(k+1) = x^(k) - f(x^(k)) / f'(x^(k))

#### 2.3.2 多元非线性方程求解法

**牛顿法**

牛顿法是一种多元非线性方程求解方法，它使用雅可比矩阵来迭代更新近似解。其公式为：

x^(k+1) = x^(k) - J(x^(k))^(-1) * f(x^(k))

**拟牛顿法**

拟牛顿法是一种比牛顿法更快的多元非线性方程求解方法，它使用近似雅可比矩阵来迭代更新近似解。

# 3. MATLAB数值计算应用

### 3.1 科学计算

#### 3.1.1 物理建模

MATLAB在物理建模中广泛应用，可用于模拟和分析各种物理现象。例如，使用MATLAB可以：

- 模拟流体动力学，预测流体流动模式和压力分布。
- 构建机械系统模型，分析运动、振动和应力分布。
- 求解电磁场问题，设计天线和电磁设备。

#### 3.1.2 化学计算

MATLAB在化学计算中也发挥着重要作用，可用于：

- 模拟化学反应，预测反应速率和产物分布。
- 分析光谱数据，识别化合物和确定其结构。
- 设计药物分子，优化其性质和活性。

### 3.2 工程计算

#### 3.2.1 机械工程

MATLAB在机械工程中广泛应用，可用于：

- 分析结构应力，优化设计以提高强度和耐用性。
- 模拟流体流动，设计高效的管道系统和热交换器。
- 控制机器人运动，实现精确和灵活的操作。

#### 3.2.2 电气工程

MATLAB在电气工程中也发挥着重要作用，可用于：

- 设计和分析电路，优化性能和稳定性。
- 模拟电磁场，设计天线和电磁设备。
- 控制电机和发电机，实现高效和可靠的运行。

### 3.3 金融计算

#### 3.3.1 风险评估

MATLAB在金融计算中广泛应用，可用于：

- 分析金融数据，识别风险和预测市场趋势。
- 构建风险模型，评估投资组合的风险敞口。
- 优化投资策略，最大化收益并降低风险。

#### 3.3.2 投资组合优化

MATLAB在投资组合优化中也发挥着重要作用，可用于：

- 构建投资组合，优化收益和风险平衡。
- 分析投资组合绩效，识别改进领域。
- 管理投资组合，动态调整资产配置以应对市场变化。

# 4. MATLAB数值计算优化

### 4.1 数值计算算法优化

#### 4.1.1 算法选择和优化

在数值计算中，算法的选择和优化至关重要。不同的算法具有不同的复杂度、精度和稳定性。因此，根据具体问题选择合适的算法非常重要。

**算法复杂度**

算法复杂度是指算法执行所需的时间或空间资源。对于大规模问题，算法复杂度尤为重要。常见的时间复杂度有 O(n)、O(n^2)、O(n^3) 等，其中 n 表示问题规模。

**算法精度**

算法精度是指算法计算结果与真实结果之间的接近程度。对于高精度要求的问题，需要选择精度较高的算法。常见的精度指标有绝对误差、相对误差等。

**算法稳定性**

算法稳定性是指算法在输入数据存在微小扰动时，输出结果的变化程度。稳定性好的算法对输入数据的扰动不敏感，输出结果变化较小。

#### 4.1.2 并行计算

并行计算是一种利用多核处理器或多台计算机同时执行任务的技术。并行计算可以显著提高数值计算的效率，尤其对于大规模问题。

**并行编程模型**

常见的并行编程模型有共享内存模型和消息传递模型。共享内存模型允许线程访问同一块内存区域，而消息传递模型需要线程通过消息传递进行通信。

**并行算法**

并行算法是专门为并行计算设计的算法。常见的并行算法有并行矩阵乘法、并行快速排序等。

### 4.2 数值计算精度优化

#### 4.2.1 浮点运算误差

浮点运算误差是由于计算机使用有限精度表示实数导致的。浮点运算误差可能导致计算结果与真实结果存在差异。

**浮点运算误差类型**

常见的浮点运算误差类型有舍入误差、截断误差和舍入误差。舍入误差是将无限精度实数转换为有限精度浮点数时产生的误差，截断误差是将有限精度浮点数转换为更低精度的浮点数时产生的误差。

**减少浮点运算误差**

减少浮点运算误差的方法包括：

* 使用更高精度的浮点数类型，如 double 而不是 float
* 避免不必要的浮点运算
* 使用舍入算法，如舍入到最接近的偶数或最接近的奇数

#### 4.2.2 数值稳定性

数值稳定性是指算法对输入数据扰动的敏感程度。数值稳定的算法在输入数据存在微小扰动时，输出结果变化较小。

**数值不稳定性**

数值不稳定性可能导致计算结果放大或缩小输入数据的扰动，从而导致严重错误。

**提高数值稳定性**

提高数值稳定性的方法包括：

* 使用条件数较小的算法
* 避免使用分母接近零的表达式
* 使用正交分解或奇异值分解等数值稳定技术

# 5.1 大规模数据处理

### 5.1.1 并行计算技术

**并行计算**是指利用多个处理器或计算机同时执行任务，以提高计算速度。MATLAB提供了多种并行计算工具，包括：

- **并行池 (Parallel Pool)**：创建一个包含多个工作进程的池，并使用 `parfor` 循环并行执行代码。
- **分布式计算引擎 (Distributed Computing Engine)**：在集群或云计算平台上分布式执行任务。
- **GPU 计算**：利用图形处理单元 (GPU) 的并行处理能力加速计算。

**并行计算步骤：**

1. **创建并行池：**使用 `parpool` 函数创建包含指定数量工作进程的并行池。
2. **并行执行代码：**使用 `parfor` 循环将代码块并行执行。
3. **获取结果：**使用 `gather` 函数从工作进程收集结果。

**示例：**

% 创建并行池
parpool(4);

% 并行计算 1000 个随机数的平均值
n = 1000;
x = rand(n, 1);
avg = parfor i = 1:n
    x(i) / n;
end

% 获取结果
avg = gather(avg);

### 5.1.2 云计算平台

**云计算平台**提供了可扩展的计算资源，可用于处理大规模数据集。MATLAB支持与以下云计算平台集成：

- **亚马逊网络服务 (AWS)**
- **微软 Azure**
- **谷歌云平台 (GCP)**

**云计算步骤：**

1. **创建云实例：**在云平台上创建虚拟机或容器实例。
2. **部署MATLAB：**将MATLAB安装到云实例上。
3. **连接到云实例：**使用MATLAB远程桌面或其他工具连接到云实例。
4. **执行并行计算：**使用MATLAB并行计算工具在云实例上并行执行代码。

**示例：**

% 连接到 AWS EC2 实例
instance = ec2connect('KeyName', 'my-key', 'Region', 'us-east-1');

% 在实例上并行计算 1000 个随机数的平均值
n = 1000;
x = rand(n, 1);
avg = parfor i = 1:n
    x(i) / n;
end

% 断开连接
ec2disconnect(instance);