【MATLAB函数值计算秘籍】：揭开数值计算背后的奥秘，从新手到大师的进阶指南

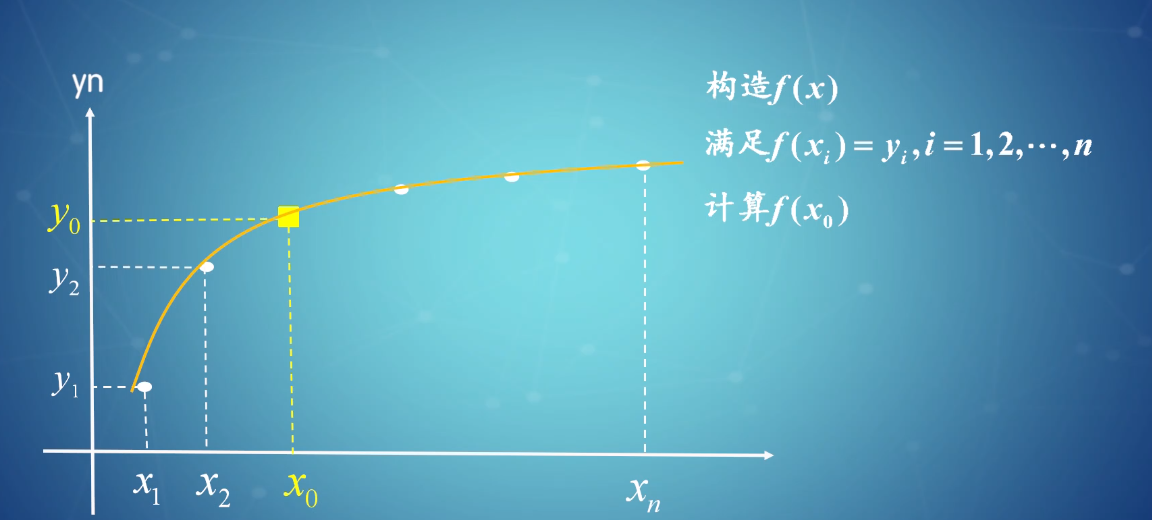
# 1. MATLAB 函数值计算的基础**

MATLAB 中的函数值计算是数值计算的基础，它允许用户计算函数在特定输入值下的值。MATLAB 提供了一系列内置函数来执行此类计算，包括用于插值、积分和求导的函数。此外，用户还可以编写自己的自定义函数来执行更复杂的计算。

函数值计算在科学、工程和金融等领域有着广泛的应用。例如，在科学研究中，函数值计算可用于拟合数据并构建模型。在工程中，它可用于求解方程组和优化设计。在金融中，它可用于计算股票价格和风险。

# 2. 数值计算的理论基础

### 2.1 数值分析简介

#### 2.1.1 误差分析

在数值计算中，误差是不可避免的。误差可以分为以下几类：

- **截断误差：**由于数值方法的近似性而产生的误差。
- **舍入误差：**由于计算机有限精度而产生的误差。
- **数据误差：**由于输入数据不准确而产生的误差。

误差分析是数值分析的重要组成部分，它可以帮助我们了解和控制数值计算中的误差。

#### 2.1.2 数值方法的分类

数值方法可以分为以下几类：

- **直接方法：**直接求解问题的精确解。
- **迭代方法：**通过逐步逼近的方式求解问题的近似解。
- **蒙特卡罗方法：**通过随机采样来求解问题的近似解。

不同的数值方法适用于不同的问题类型。

### 2.2 函数值计算的数学原理

#### 2.2.1 插值法

插值法是通过已知函数在几个点上的值来估计函数在其他点上的值。常用的插值方法有：

- **线性插值：**通过两个已知点作一条直线，来估计函数在其他点上的值。
- **二次插值：**通过三个已知点作一个二次多项式，来估计函数在其他点上的值。
- **样条插值：**通过多个已知点作一个分段多项式，来估计函数在其他点上的值。

#### 2.2.2 数值积分

数值积分是通过近似的方式计算积分值。常用的数值积分方法有：

- **梯形法：**将积分区间等分成多个小梯形，并计算每个小梯形的面积之和来近似积分值。
- **辛普森法：**将积分区间等分成多个小抛物线，并计算每个小抛物线的面积之和来近似积分值。
- **高斯求积法：**使用高斯求积公式来近似积分值。

#### 2.2.3 数值求导

数值求导是通过近似的方式计算导数值。常用的数值求导方法有：

- **前向差分法：**使用函数在当前点和前一个点的值来近似导数值。
- **后向差分法：**使用函数在当前点和后一个点的值来近似导数值。
- **中心差分法：**使用函数在当前点的前一个点和后一个点的值来近似导数值。

% 使用中心差分法计算导数值
f = @(x) x^2;
x = 1;
h = 0.01;
df_dx = (f(x + h) - f(x - h)) / (2 * h);
disp(df_dx);

**代码逻辑分析：**

1. 定义函数 `f`，计算 x 的平方。
2. 设置 x 的值和步长 h。
3. 使用中心差分公式计算导数值 `df_dx`。
4. 输出导数值。

**参数说明：**

- `f`: 要计算导数的函数。
- `x`: 要计算导数的点。
- `h`: 步长。

# 3.1 内置函数的使用

MATLAB 提供了丰富的内置函数来执行函数值计算任务，这些函数可以有效地处理各种数值计算问题。

#### 3.1.1 插值函数

插值函数用于根据一组已知数据点估计中间值。MATLAB 提供了多种插值函数，包括：

- `interp1`：一维线性插值
- `interp2`：二维线性插值
- `spline`：三次样条插值
- `pchip`：分段三次样条插值

% 一维线性插值
x = [0, 1, 2, 3];
y = [0, 1, 4, 9];
x_interp = 1.5;
y_interp = interp1(x, y, x_interp);

% 显示插值结果
disp(['插值结果：', num2str(y_interp)]);

#### 3.1.2 积分函数

积分函数用于计算函数在给定区间上的积分。MATLAB 提供了以下积分函数：

- `integral`：数值积分
- `quad`：自适应数值积分
- `trapz`：梯形积分

% 数值积分
f = @(x) x.^2;
a = 0;
b = 1;
result = integral(f, a, b);

% 显示积分结果
disp(['积分结果：', num2str(result)]);

#### 3.1.3 求导函数

求导函数用于计算函数的导数。MATLAB 提供了以下求导函数：

- `diff`：数值求导
- `gradient`：多维数组的梯度
- `symdiff`：符号求导

% 数值求导
f = @(x) x.^3;
x_val = 2;
derivative = diff(f, x_val);

% 显示求导结果
disp(['导数结果：', num2str(derivative)]);

# 4. 函数值计算的进阶应用

### 4.1 拟合和建模

#### 4.1.1 数据拟合

数据拟合是根据给定的数据点找到一条或多条曲线，以近似表示这些数据。MATLAB 提供了多种内置函数用于数据拟合，例如 `polyfit`、`fit` 和 `curvefit`。

% 给定数据点
data = [1, 2; 3, 4; 5, 6; 7, 8];

% 使用 polyfit 进行多项式拟合
p = polyfit(data(:,1), data(:,2), 1);

% 拟合曲线
x = linspace(1, 7, 100);
y = polyval(p, x);

% 绘制拟合曲线和原始数据
plot(data(:,1), data(:,2), 'o', x, y, '-');
xlabel('x');
ylabel('y');
legend('原始数据', '拟合曲线');

**参数说明：**

* `polyfit(x, y, n)`：进行 n 阶多项式拟合，其中 x 和 y 是数据点的横纵坐标。
* `linspace(a, b, n)`：生成从 a 到 b 的 n 个均匀间隔的点。
* `polyval(p, x)`：使用多项式系数 p 计算 x 处的拟合值。

**逻辑分析：**

1. `polyfit` 函数根据给定的数据点计算多项式系数 p。
2. `linspace` 函数生成均匀间隔的 x 值，用于绘制拟合曲线。
3. `polyval` 函数使用 p 计算每个 x 值对应的拟合 y 值。
4. 最后，将原始数据和拟合曲线绘制在同一张图上，以可视化拟合效果。

#### 4.1.2 模型构建

模型构建是指基于数据或理论知识建立数学模型，以描述和预测系统行为。MATLAB 提供了 `simulink` 和 `stateflow` 等工具箱，用于创建和仿真复杂模型。

% 创建一个简单的二阶系统模型
sys = tf([1, 2, 1], [1, 3, 2]);

% 仿真模型的阶跃响应
t = linspace(0, 10, 100);
[y, t] = step(sys, t);

% 绘制阶跃响应
plot(t, y);
xlabel('时间 (s)');
ylabel('输出');
title('二阶系统阶跃响应');

**参数说明：**

* `tf(num, den)`：创建传递函数，其中 num 和 den 是分子和分母多项式系数。
* `step(sys, t)`：仿真系统 sys 在时间 t 处的阶跃响应。

**逻辑分析：**

1. `tf` 函数创建传递函数 sys，表示二阶系统的数学模型。
2. `step` 函数仿真 sys 在时间 t 处的阶跃响应，得到输出 y。
3. 最后，将阶跃响应绘制在图上，以可视化系统对阶跃输入的反应。

### 4.2 数值求解

#### 4.2.1 方程组求解

MATLAB 提供了多种方法来求解方程组，包括直接求解、迭代求解和稀疏求解。对于直接求解，可以使用 `inv` 函数求解线性方程组，对于迭代求解，可以使用 `gmres` 和 `bicgstab` 函数。

% 定义方程组系数矩阵和右端向量
A = [2, 1; 3, 4];
b = [5; 6];

% 使用 inv 函数直接求解
x = inv(A) * b;

% 使用 gmres 函数迭代求解
[x, flag, relres, iter, resvec] = gmres(A, b);

**参数说明：**

* `inv(A)`：求解线性方程组 A*x = b。
* `gmres(A, b)`：使用广义最小残量 (GMRES) 方法迭代求解方程组 A*x = b。

**逻辑分析：**

1. `inv` 函数直接求解方程组，得到解 x。
2. `gmres` 函数使用 GMRES 算法迭代求解方程组，并返回解 x、收敛标志 flag、相对残差 relres、迭代次数 iter 和残差向量 resvec。

#### 4.2.2 最优化问题求解

MATLAB 提供了多种优化算法来求解最优化问题，包括无约束优化、约束优化和全局优化。对于无约束优化，可以使用 `fminunc` 函数，对于约束优化，可以使用 `fmincon` 函数，对于全局优化，可以使用 `ga` 和 `pso` 函数。

% 定义目标函数
fun = @(x) x^2 + 2*x + 1;

% 使用 fminunc 函数求解无约束优化问题
x0 = 0;  % 初始点
options = optimset('Display', 'iter');  % 设置优化选项
[x, fval] = fminunc(fun, x0, options);

**参数说明：**

* `fun`：目标函数。
* `fminunc(fun, x0, options)`：使用无约束优化算法 fminunc 求解目标函数 fun，其中 x0 是初始点，options 是优化选项。

**逻辑分析：**

1. `fminunc` 函数使用无约束优化算法求解目标函数 fun，并返回最优解 x 和最优值 fval。
2. `optimset` 函数设置优化选项，例如 `Display` 选项用于控制优化过程的显示方式。

# 5. MATLAB 函数值计算的调试和优化

### 5.1 调试技巧

**5.1.1 断点调试**

断点调试是一种在特定代码行暂停程序执行的技术，以便检查变量的值和程序状态。在 MATLAB 中，可以使用 `dbstop` 函数设置断点。例如：

% 在第 10 行设置断点
dbstop('myFunction', 10);

**5.1.2 代码跟踪**

代码跟踪允许您逐步执行程序，并检查每个步骤中的变量值。在 MATLAB 中，可以使用 `dbcont` 函数执行代码跟踪。例如：

% 逐行执行代码
dbcont;

**5.1.3 错误处理**

MATLAB 提供了广泛的错误处理功能，允许您捕获和处理运行时错误。可以使用 `try-catch` 语句块捕获错误，并执行相应的操作。例如：

try
    % 执行可能引发错误的代码
catch err
    % 捕获错误并执行操作
    disp(err.message);
end

### 5.2 优化策略

**5.2.1 代码优化**

* **矢量化操作：**使用矢量化操作可以提高代码效率，因为它可以同时对数组中的多个元素进行操作。例如：

% 使用矢量化操作计算数组元素的平方
y = x.^2;

* **预分配内存：**预分配内存可以减少 MATLAB 在运行时分配和释放内存的开销。例如：

% 预分配一个 1000 x 1000 的矩阵
A = zeros(1000, 1000);

* **避免不必要的循环：**使用矩阵操作或矢量化操作可以避免不必要的循环，提高代码效率。例如：

% 使用矩阵操作计算矩阵元素的总和
sum_matrix = sum(A, 2);

**5.2.2 内存优化**

* **使用稀疏矩阵：**稀疏矩阵可以存储大量零元素的矩阵，从而节省内存。例如：

% 创建一个稀疏矩阵
S = sparse(1000, 1000);

* **使用结构体和类：**结构体和类可以将相关数据组织在一起，并允许有效地访问和修改数据。例如：

% 创建一个包含学生信息的结构体
student = struct('name', 'John', 'age', 20, 'gpa', 3.5);

**5.2.3 并行计算**

MATLAB 支持并行计算，允许您在多个处理器或内核上分布计算任务。例如：

% 使用并行计算求解方程组
A = randn(1000, 1000);
b = randn(1000, 1);
x = A \ b;

# 6. MATLAB 函数值计算的应用案例**

MATLAB 函数值计算在各个领域都有广泛的应用，以下列举几个典型的案例：

**6.1 数据分析**

MATLAB 提供了强大的数据分析工具，可以高效地处理和分析大量数据。例如，我们可以使用 `fitlm` 函数对数据进行线性回归，并使用 `plot` 函数绘制拟合曲线。

% 导入数据
data = importdata('data.csv');

% 拟合线性回归模型
model = fitlm(data(:,1), data(:,2));

% 绘制拟合曲线
plot(data(:,1), data(:,2), 'o');
hold on;
plot(data(:,1), model.Fitted, 'r-');
legend('数据点', '拟合曲线');
xlabel('x');
ylabel('y');

**6.2 机器学习**

MATLAB 是机器学习算法开发和部署的理想平台。我们可以使用 `train` 函数训练分类器，并使用 `predict` 函数对新数据进行预测。

% 导入数据
data = importdata('data.csv');

% 划分训练集和测试集
[trainData, testData] = dividerand(data, 0.7, 0.3);

% 训练分类器
classifier = train(trainData, 'class');

% 对测试集进行预测
predictions = predict(classifier, testData);

**6.3 图像处理**

MATLAB 提供了丰富的图像处理工具，可以用于图像增强、特征提取和对象识别。例如，我们可以使用 `imfilter` 函数对图像进行滤波，并使用 `edge` 函数检测图像中的边缘。

% 导入图像
image = imread('image.jpg');

% 滤波图像
filteredImage = imfilter(image, fspecial('gaussian', 5, 1));

% 检测边缘
edges = edge(filteredImage, 'canny');

% 显示原图和边缘检测结果
subplot(1,2,1);
imshow(image);
title('原图');
subplot(1,2,2);
imshow(edges);
title('边缘检测结果');

**6.4 科学研究**

MATLAB 在科学研究中扮演着至关重要的角色，可以用于数值模拟、数据可视化和结果分析。例如，我们可以使用 `ode45` 函数求解微分方程，并使用 `plot` 函数绘制解的图像。

% 定义微分方程
dydt = @(t, y) y - t^2 + 1;

% 求解微分方程
[t, y] = ode45(dydt, [0, 1], 1);

% 绘制解的图像
plot(t, y);
xlabel('t');
ylabel('y');
title('微分方程的解');