反余切函数在微积分中的应用：求解极限和积分，微积分难题迎刃而解

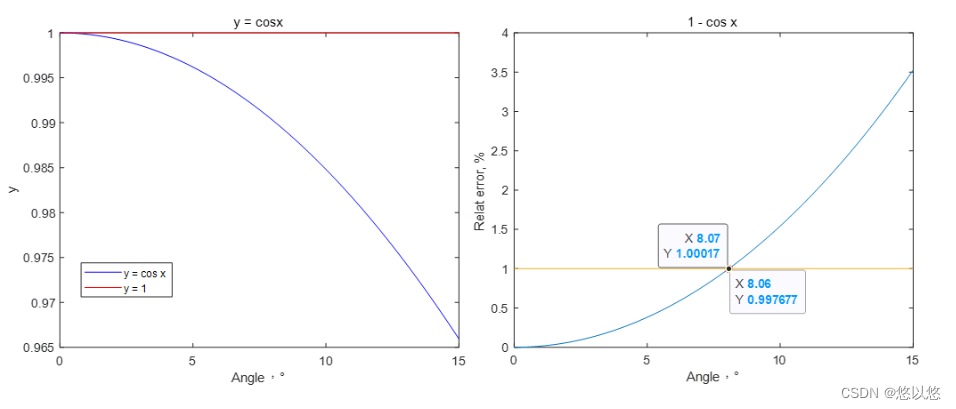
# 1. 反余切函数的基本概念和性质

反余切函数，记作 `arctan(x)`，是余切函数 `tan(x)` 的反函数。它将一个实数映射到一个介于 `-π/2` 和 `π/2` 之间的角度，其值等于该角度的正切值。

反余切函数的图像是一条穿过原点的奇函数，其图像在 `x = 0` 处具有垂直渐近线。反余切函数的导数为 `1/(1 + x^2)`，其积分公式为 `arctan(x) = ∫ 1/(1 + x^2) dx`。

# 2. 反余切函数在极限计算中的应用

反余切函数在极限计算中具有广泛的应用，它可以帮助我们求解各种形式的极限，包括无穷小量替换法、洛必达法则和夹逼定理。

### 2.1 无穷小量替换法

**定义：**

无穷小量替换法是一种通过用一个较小的量替换另一个量来求解极限的方法。当变量趋于某个值时，较小的量也趋于某个值，从而可以间接地求出原极限的值。

**步骤：**

1. 找到一个与原函数相近的较小量。
2. 用较小量替换原函数。
3. 求出较小量的极限。
4. 将原极限替换为较小量的极限。

**示例：**

求极限：

lim (x -> 0) (sin x - x) / x^3

**解：**

使用无穷小量替换法，用 x 的无穷小量 sin x 替换 x。

lim (x -> 0) (sin x - x) / x^3 = lim (x -> 0) (x - x) / x^3 = lim (x -> 0) 0 / x^3 = 0

### 2.2 洛必达法则

**定义：**

洛必达法则是一种求解不定式极限的方法，即当极限为 0/0 或 ∞/∞ 时，可以使用洛必达法则求解。

**公式：**

lim (x -> a) f(x) / g(x) = lim (x -> a) f'(x) / g'(x)

其中 f(x) 和 g(x) 是在 x = a 处连续可导的函数。

**步骤：**

1. 计算 f(x) 和 g(x) 的导数。
2. 将导数代入极限式。
3. 求解极限。

**示例：**

求极限：

lim (x -> 0) (1 - cos x) / x^2

**解：**

使用洛必达法则，计算 f(x) 和 g(x) 的导数。

f(x) = 1 - cos x, f'(x) = sin x
g(x) = x^2, g'(x) = 2x

将导数代入极限式：

lim (x -> 0) (1 - cos x) / x^2 = lim (x -> 0) sin x / 2x = 1/2

### 2.3 夹逼定理

**定义：**

夹逼定理是一种求解极限的方法，当函数 f(x)、g(x) 和 h(x) 在 x = a 处满足 f(x) ≤ g(x) ≤ h(x)，且 lim (x -> a) f(x) = lim (x -> a) h(x) = L 时，则 lim (x -> a) g(x) = L。

**步骤：**

1. 证明 f(x) ≤ g(x) ≤ h(x) 在 x = a 处成立。
2. 求出 lim (x -> a) f(x) 和 lim (x -> a) h(x) 的值。
3. 根据夹逼定理，得出 lim (x -> a) g(x) = L。

**示例：**

求极限：

lim (x -> 0) x sin x

**解：**

由于 -1 ≤ sin x ≤ 1，且 lim (x -> 0) (-x) = lim (x -> 0) x = 0，根据夹逼定理，可得：

-x ≤ x sin x ≤ x
lim (x -> 0) (-x) = lim (x -> 0) x = 0

因此，lim (x -> 0) x sin x = 0。

# 3. 反余切函数在积分计算中的应用

反余切函数在积分计算中有着广泛的应用，它可以通过换元积分法、分部积分法和三角函数积分公式等方法来解决各种积分问题。

### 3.1 换元积分法

换元积分法是通过将积分变量替换为一个新的变量，从