信号分析中的特征提取：从数据中挖掘价值，洞察信号内涵

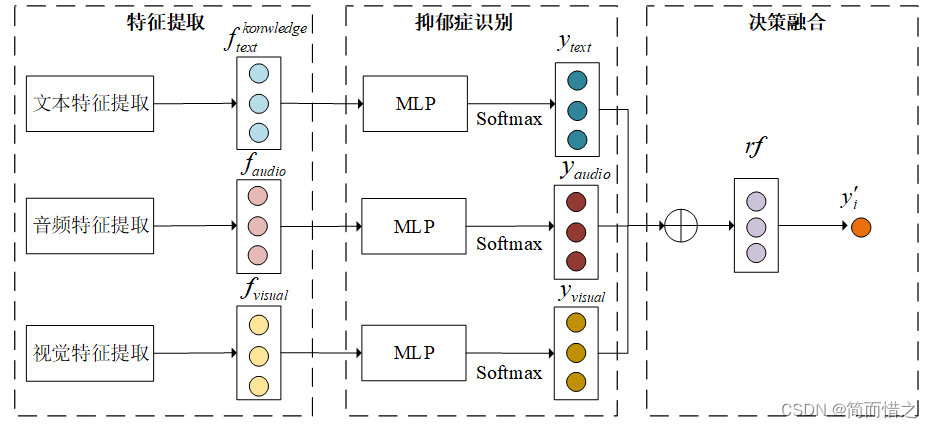
# 1. 信号分析概述

信号分析是处理和解释信号的过程，信号是携带信息的物理量。信号分析广泛应用于各个领域，如通信、医疗、工业和金融。

信号分析的目标是提取信号中的特征，这些特征可以用来识别、分类和理解信号。信号特征可以分为时域特征和频域特征。时域特征描述信号在时间上的变化，而频域特征描述信号在频率上的分布。

# 2. 信号特征提取理论基础

### 2.1 时域特征提取

时域特征提取是指从信号的时间序列中提取特征。时域特征反映了信号在时间轴上的变化规律，可以用于描述信号的幅度、频率和相位等基本属性。

#### 2.1.1 均值、方差和标准差

均值、方差和标准差是时域特征提取中最常用的统计量。

- **均值**反映了信号的平均值，可以用来衡量信号的整体强度。
- **方差**反映了信号的离散程度，可以用来衡量信号的波动性。
- **标准差**是方差的平方根，具有与方差相同的单位，可以用来衡量信号的离散程度。

import numpy as np

# 计算均值
mean = np.mean(signal)

# 计算方差
variance = np.var(signal)

# 计算标准差
std = np.std(signal)

#### 2.1.2 自相关和互相关

自相关和互相关是时域特征提取中常用的相关性度量。

- **自相关**衡量信号与自身在不同时间偏移下的相关性。自相关函数可以用来识别信号中的周期性或重复性模式。
- **互相关**衡量两个信号在不同时间偏移下的相关性。互相关函数可以用来识别两个信号之间的相似性或相关性。

import numpy as np

# 计算自相关
autocorr = np.correlate(signal, signal, mode='full')

# 计算互相关
crosscorr = np.correlate(signal1, signal2, mode='full')

### 2.2 频域特征提取

频域特征提取是指从信号的频率谱中提取特征。频域特征反映了信号在频率轴上的分布规律，可以用于描述信号的频率成分和能量分布。

#### 2.2.1 傅里叶变换和功率谱密度

傅里叶变换是将时域信号转换为频域信号的数学工具。功率谱密度是傅里叶变换的平方模，反映了信号在不同频率上的能量分布。

import numpy as np
from scipy.fftpack import fft

# 计算傅里叶变换
fft_signal = fft(signal)

# 计算功率谱密度
psd = np.abs(fft_signal) ** 2

#### 2.2.2 小波变换和时频分析

小波变换是一种时频分析工具，可以将信号分解为不同尺度和频率的子带。时频分析可以同时显示信号在时间轴和频率轴上的变化规律。

im