频率特性深入分析：模拟电路中的频率响应掌握技巧


参考资源链接：[模拟集成电路的分析与设计（第4版）答案](https://wenku.csdn.net/doc/6401ac32cce7214c316eaf87?spm=1055.2635.3001.10343)
# 1. 频率特性的理论基础

在电子工程领域，频率特性是描述系统在不同频率信号作用下性能变化的重要指标。理解频率特性的理论基础是掌握电路设计和分析的关键。本章将介绍与频率特性相关的基础理论，包括信号在电子系统中的传播方式、频率域分析的基本概念以及信号处理中常用的一些数学模型。

## 1.1 频率特性的基本概念

频率特性主要描述了一个信号处理系统如何响应不同频率的输入信号。系统可能对某些频率的信号放大或者衰减，这种差异性就称为频率特性。在数学上，可以通过傅里叶变换将信号分解成一系列不同频率的正弦波，进一步研究每个频率成分在系统中的传递情况。

## 1.2 傅里叶分析基础

傅里叶分析是研究频率特性的基础，它允许我们把任何周期性或者非周期性的时间信号转化为频域中的一系列频率分量。通过傅里叶变换，信号的时域特性被转化为频域特性，其中包含了幅值和相位两个维度的信息。

## 1.3 信号的频域表示

在频域中，信号由其频率分量的幅值和相位构成，这种表示形式称为频谱。频谱可以清晰地展示出信号在不同频率下的能量分布，对于分析系统的频率特性提供了直观的视角。通过对频谱的分析，我们可以更深入地理解信号的特性和系统的响应行为。

## 1.4 传递函数与频率响应

传递函数描述了系统输入和输出信号之间的关系，是频域分析中的核心概念。通过传递函数，可以计算出系统对于不同频率信号的响应，也就是频率响应。频率响应分析能够揭示系统在处理特定频率信号时的性能表现，是设计电子系统时必须考虑的因素。

总结而言，频率特性理论基础为我们后续深入学习频率响应在模拟电路中的应用提供了必要的理论支撑。通过本章内容，我们了解了频率特性的重要性，并对傅里叶分析和传递函数等基础概念有了初步的认识，为后续章节的学习打下了坚实的理论基础。

# 2. 模拟电路的频率响应概念

## 2.1 频率响应的基本定义

### 2.1.1 传递函数与频率响应的关系

在模拟电路中，传递函数定义了电路的输出与输入之间的比率关系，其形式一般为复频域中的有理分式。传递函数可以用来描述电路对不同频率信号的放大或衰减能力，它是一个复数函数，其中分子代表输出信号的复幅值，而分母则体现了信号通过电路时可能遇到的抑制或增强特性。

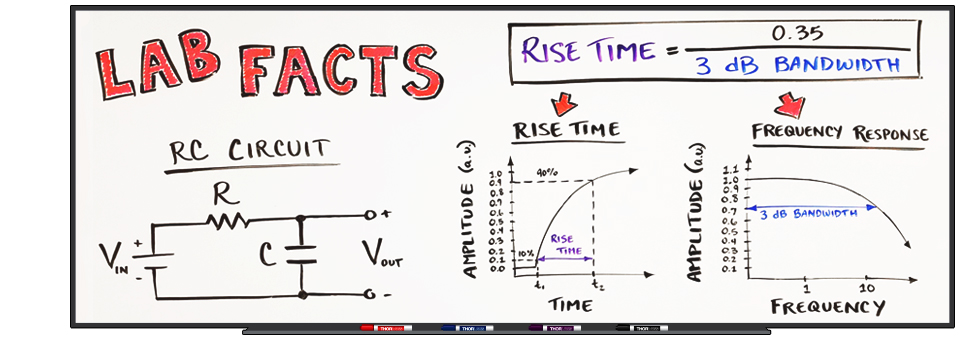
为了便于理解，我们可以通过一个简单的RC低通滤波器的传递函数来分析频率响应：

\[ H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{RCs + 1} \]

其中，\( V_{out}(s) \)和\( V_{in}(s) \)分别表示输出和输入信号的拉普拉斯变换（s域），\( R \)和\( C \)分别是电阻和电容的值，\( s \)是复频域变量。这个传递函数描述了当输入信号频率增加时，输出信号幅度会降低，即电路具有低通滤波特性。通过分析传递函数的频率依赖部分，即\( s \)的函数，可以推导出频率响应。

### 2.1.2 极点与零点对频率响应的影响

在复频域分析中，传递函数中的极点和零点对于确定电路频率响应至关重要。

- **极点**：极点是传递函数分母多项式中\( s \)的值使得传递函数趋向无穷大的点。在模拟电路中，极点通常对应于电路的时间常数，并决定了电路的自然响应速率。例如，RC低通滤波器中的\( -\frac{1}{RC} \)就是一个极点。
- **零点**：零点是传递函数分子多项式中\( s \)的值使得传递函数等于零的点。零点决定了特定频率处的增益特性。零点可以用来抵消某些极点的不利影响，或者在特定频率提供额外的增益。

在RC低通滤波器中，如果我们在输出端加入一个电压跟随器（一个缓冲器），则可以在\( s = 0 \)处添加一个零点，这有助于改善低频区的相位响应。通过添加零点和极点，我们可以精心设计电路以获得特定的频率响应特性。

## 2.2 频率响应的图形表示

### 2.2.1 幅频特性曲线（Bode图）

Bode图是描述模拟电路频率响应的一种常用方法，它由两个图组成：幅频图和相频图。幅频图显示了电路对不同频率信号的增益（幅度）变化，而相频图显示了相位变化。

幅频特性曲线通常使用对数刻度来表示频率和增益的关系，使得频率范围很大的电路特性可以直观展示在有限的图表空间内。该图的横轴是频率的对数，纵轴是增益（分贝，dB）的线性尺度。

以RC低通滤波器为例，其幅频特性可以表示为：

\[ 20 \log_{10} \left| H(j\omega) \right| = 20 \log_{10} \left| \frac{1}{\sqrt{1 + (\omega RC)^2}} \right| \]

其中\( \omega \)是角频率，\( j \)是虚数单位。通过绘制这个关系，我们可以得到一个典型的低通滤波器的幅频特性曲线，它在频率低时增益接近1（0 dB），随着频率增加而逐渐降低。

### 2.2.2 相频特性曲线

相频特性曲线显示了信号通过电路后相位移动的变化情况。对于RC低通滤波器，其相位移动可以表示为：

\[ \angle H(j\omega) = -\arctan(\omega RC) \]

在低频时，相位移动接近0度，随着频率增加，相位移动逐渐趋向-90度。

## 2.3 影响频率响应的因素

### 2.3.1 元件参数的变化

模拟电路中使用的电阻、电容和电感等元件的参数值不是恒定不变的，会受到温度、老化和其他环境因素的影响，从而影响频率响应。

例如，电阻值可能会由于温度的升高而增加；电容的介电材料在不同的温度和湿度条件下其介电常数会发生变化，进而改变电容值；电感器也可能因为磁芯材料的非线性特性而影响其工作频率范围。因此，设计时需要对这些潜在的变化进行考虑，以保证电路在指定的工作条件下性能稳定。

### 2.3.2 外部环境对频率响应的影响

外部环境，包括电源噪声、电磁干扰（EMI）、温度变化等，都可能对模拟电路的频率响应产生影响。

- **电源噪声**：开关电源或不稳定电源会产生噪声，这些噪声叠加在电路的信号上，可以改变电路的频率响应，特别是在高频部分。
- **电磁干扰（EMI）**：EMI可以通过辐射或感应耦合进入电路，尤其是对高频电路影响较大。通过合理布局和使用屏蔽、滤波等技术，可以减少这种影响。
- **温度变化**：温度的变化会影响元件的电气特性，进而影响电路的频率响应。

在设计电路时，上述因素都需要纳入考虑，以确保电路在实际工作环境中的稳定性和可靠性。通过对电路的环境敏感性分析和测试，可以对电路进行适当调整或增加保护措施，以提高电路在各种条件下的频率响应性能。

# 3. 频率特性分析工具与方法

## 3.1 分析工具的选择与应用

### 3.1.1 电路仿真软件的使用技巧

随着技术的进步，电路设计和分析工具已经发展到非常高级的阶段。电路仿真软件为工程师提供了强大的平台，能够进行复杂电路的频率特性分析。在众多可用的仿真软件中，SPICE（Simulation Program with Integrated Circuit Emphasis）及其衍生版本是最常见的选择。

在使用SPICE类软件时，首先要创建电路的网表（netlist），这是一个包含所有元件参数和连接关系的文本文件。例如，在LTspice中创建一个简单的RC电路网表，可以按照以下步骤进行：

*LTspice
V1 in 0 SIN(0 1 1k) ; 1kHz sine wave voltage source
R1 in out 1k ; 1kOhm resistor
C1 out 0 1u ; 1uF capacitor
.ac dec 10 1 10k ; frequency sweep from 1Hz to 10kHz, 10 points/decade
.plot mag(V(out))

这里，`.ac` 指令用于设置交流分析，其中`dec`表示频率扫描的类型是十进制，数字10表示每十年的点数，1和10k定义了扫描的频率范围。`plot`指令用于生成输出电压的幅度响应。

仿真软件能够通过这种方式快速地给出电路的频率响应，无需实际搭建电路，节省时间和成本。软件中的模拟器会计算出每个频率点的电路响应，然后生成Bode图、幅度响应曲线等，工程师可以直观地看到电路的频率特性。

### 3.1.2 实验室仪器在频率分析中的应用

尽管仿真软件功能强大，但实际硬件测试仍然是必不可少的步骤。频谱分析仪和网络分析仪是实验室中用于频率分析的关键工具。

频谱分析仪能够测量信号的频率组成和幅度信息，其应用范围广泛，从音频到微波频段的信号都可以分析。在测量信号频率特性时，频谱分析仪可以提供信号的幅度谱和相位谱。

网络分析仪主要用于测量射频(RF)和微波电路的S参数。它能够同时进行幅度和相位的测量，并自动转换成其他常用的参数，如增益、相位延迟等。利用网络分析仪进行频率响应测量，可以得到更精确和详细的频率特性数据。

在使用这些仪器时，正确设置仪器参数是关键。需要考虑的因素包括频率范围、分辨率带宽、扫描时间、参考电平、输入衰减等。在实际操作中，工程师应遵循设备的使用手册，确保测试数据的准确性和重复性。

## 3.2 频率响应的测量技术

### 3.2.1 频率扫描法

频率扫描法是一种广泛应用于频率特性测量的技术。它通过改变输入信号的频率，并记录输出信号与输入信号的比率，从而得到电路的幅频和相频特性。在实际操作中，可以使用函数发生器来生成不同频率的信号，并用示波器或频谱分析仪来观测响应。

一个典型的频率扫描过程如下：

1. 准备一个信号源，可以是一个函数发生器。
2. 设置信号源的频率范围和步进值。
3. 使用示波器或频谱分析仪测量每个频率点的输出幅度。
4. 记录数据并绘制Bode图。

### 3.2.2 瞬态响应分析法

瞬态响应分析法是另一种测量频率特性的技术。不同于频率扫描法，瞬态分析关注的是电路对一个非周期性瞬态输入（如阶跃函数或脉冲）的响应。

进行瞬态响应分析的基本步骤如下：

1. 为电路施加一个阶跃输入信号。
2. 使用示波器记录电路的瞬态输出。
3. 通过傅里叶变换将时域信号转换为频域信号。
4. 分析电路的频率特性。

## 3.3 分析方法的深入探讨

### 3.3.1 时域与频域分析的对比

在电子学中，时域分析和频域分析是两种基本的分析方法。时域分析关注的是信号随时间变化的特性，而频域分析则关注信号的频率成分。

时域分析如瞬态响应测试，它直接提供了关于电路对输入脉冲或阶跃信号响应的信息，适合于分析电路的稳定性和瞬态行为。频域分析则帮助工程师了解电路对不同频率信号的放大或衰减特性，这对于滤波器设计和信号完整性分析尤为重要。

例如，使用频谱分析仪进行频域测量，可以查看一个电路在各个频率上的幅度和相位特性，这是时域方法无法直接提供的信息。在设计滤波器或进行通信系统分析时，频域信息是不可或缺的。

### 3.3.2 多参数影响下的分析策略

在实际电路设计中，许多参数可能会对频率特性产生影响。例如，一个放大器的带宽和增益不仅受内部电路设计的影响，也与晶体管的选择、电源电压、温度等因素有关。

面对多参数的影响，工程师需要制定出一套有效的分析策略。这通常包括以下步骤：

1. 确定关键参数：识别对电路性能影响最大的参数。
2. 参数扫描：对关键参数进行系统性的扫描，以了解它们如何影响电路性能。
3. 交互分析：对相互影响的参数进行联合分析，确定最佳的设计点。
4. 实验验证：通过实验验证仿真和分析的结果，调整设计以获得预期性能。

采用上述策略，可以确保电路设计在各种条件下均能达到最佳性能。这是提高设计效率和电路性能的重要手段。

以上内容仅为第三章部分内容的缩略示例。每章节的内容都应该按照这一标准，结合Markdown格式中的表格、代码块、流程图等元素进行详细展开，以达到2000字的一级章节内容要求。

# 4. 模拟电路设计中的频率优化

## 4.1 设计策略与频率优化

### 4.1.1 滤波器设计原理

在模拟电路设计中，滤波器是用于选择性地允许或抑制特定频率范围内的信号的重要组件。滤波器根据其设计目标可以分为低通、高通、带通和带阻等类型。滤波器设计的关键在于其传递函数的选择，传递函数决定了滤波器的