【优先队列的扩展】：构建满足特定需求的自定义优先队列

# 1. 优先队列的概念与基础实现

在计算机科学中，优先队列是一种抽象数据类型，它允许插入数据元素，并能迅速检索出具有最高优先级的元素。相比标准队列，它使得队列中的元素可以按照任何优先级顺序进行处理，而不仅仅是按照先进先出（FIFO）的顺序。

## 2.1 优先队列的基本概念

### 2.1.1 优先队列的定义
优先队列可以简单地定义为一种允许插入数据元素，同时允许检索和删除当前优先级最高的元素的数据结构。它模拟了现实中的一些场景，比如紧急任务总是先执行。

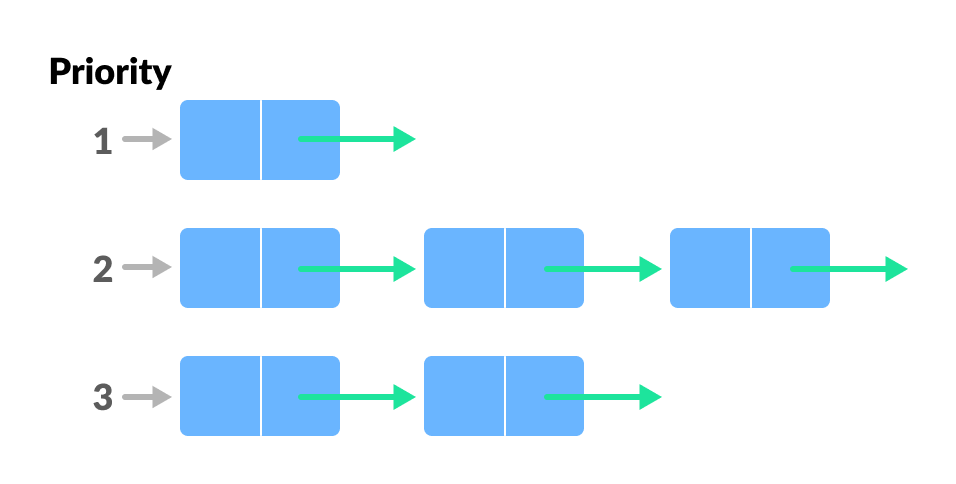
### 2.1.2 优先队列的工作原理
优先队列的实现通常依赖于堆数据结构。在堆中，元素按照优先级排序，最高优先级的元素位于堆顶。检索（获取但不删除）和删除操作通常发生在堆顶元素。

优先队列是很多高级算法和数据结构（如图算法、排序算法）的重要组成部分，应用广泛，从操作系统任务调度到各种网络服务。

在下一章，我们将深入探讨优先队列的理论基础，包括它的数学模型和常见实现方式，帮助您更好地理解优先队列的原理和应用。

# 2. 理解优先队列的理论基础

### 2.1 优先队列的基本概念

#### 2.1.1 优先队列的定义

在计算机科学中，优先队列是一种抽象数据类型，与普通队列类似，允许用户插入新的对象，并从队列中移除“最高优先级”的元素。然而，与标准队列操作不同的是，优先队列中元素的移除顺序不是由它们插入的顺序决定的，而是由它们的优先级决定。在大多数实现中，优先级最高的元素将是最先被移除的元素。优先队列通常用于任务调度、事件驱动模拟、优先级邮件队列、A*搜索算法等场景。

#### 2.1.2 优先队列的工作原理

优先队列的工作原理类似于现实生活中的紧急待办事项列表。想象一下，如果有多个任务需要完成，我们会根据每个任务的紧迫性或重要性来优先处理。优先队列就是这样一个机制，在其内部，每个元素都会有一个关联的优先级，优先级最高的元素排在队列的最前面。当需要取出一个元素时，系统会检查所有元素的优先级，并取出优先级最高的那个元素。

### 2.2 优先队列的数学模型

#### 2.2.1 堆（Heap）结构简介

堆是一种特殊的完全二叉树，其中每个节点的值都大于或等于其子节点的值（这样的堆被称为最大堆），或者每个节点的值都小于或等于其子节点的值（最小堆）。堆结构常用来实现优先队列，因为堆的性质可以保证堆顶元素总是整个树中的最大元素（对于最大堆）或最小元素（对于最小堆），这使得每次取出优先级最高元素的操作可以在O(1)的时间复杂度内完成。

#### 2.2.2 堆排序算法

堆排序是一种基于比较的排序算法，使用了二叉堆的概念。堆排序的工作原理如下：
1. 首先，将输入数据构建成一个最大堆。
2. 然后，由于最大堆的根节点是最大的元素，将其与最后一个元素交换，这样最大的元素就移到了数组的末尾。
3. 接着，缩小堆的范围，排除掉最后一个元素（已经放置在正确的位置上），再将剩下的元素重新调整为最大堆。
4. 重复步骤2和3，直到堆的大小减小到1，此时所有元素都已排序完成。

堆排序的时间复杂度为O(nlogn)，在平均和最坏的情况下都有相同的性能表现。

### 2.3 常见的优先队列实现

#### 2.3.1 标准库中的优先队列实现

在诸如C++的STL（Standard Template Library）或Java的Collection框架中，都提供了优先队列的实现。例如，在C++中，可以使用`<queue>`头文件中的`priority_queue`类，它默认使用一个最大堆来存储元素，通过一个比较器来定义元素间的优先级关系。使用标准库实现优先队列是一种简单且高效的解决方案，但可能无法满足特定场景下的所有需求，比如并发处理或是自定义数据结构的特定实现。

#### 2.3.2 时间复杂度分析

优先队列的常见操作包括插入（push）、删除（pop）以及查看堆顶元素（top）。对于使用堆实现的优先队列，这些操作的时间复杂度如下：
- 插入操作（push）：O(logn)，因为需要将新元素添加到堆中，然后可能需要执行堆的调整操作来维持堆的性质。
- 删除操作（pop）：O(logn)，需要将堆顶元素与最后一个元素交换，然后从堆中移除最后一个元素，并调整堆。
- 查看堆顶元素（top）：O(1)，查看堆顶元素（最大或最小元素）并不需要移动或删除任何元素，因此时间复杂度较低。

通过使用堆数据结构，优先队列实现了有效的动态优先级管理，为各种应用程序提供了高效的优先级处理能力。

# 3. 自定义优先队列的需求分析

在现代的计算机科学和软件工程中，优先队列是一种特殊的数据结构，它允许插入一组元素，并且每次可以从集合中取出一个"优先级最高"的元素。这种数据结构广泛应用于各种场景，比如操作系统任务调度、网络路由选择、事件驱动系统等等。在本章节中，我们将着重分析特定应用中的优先队列需求，探讨自定义优先队列的设计原则，并给出一些场景实例。

## 3.1 分析特定应用的优先队列需求

### 3.1.1 需求收集与分类

对于优先队列来说，不同的应用场景往往会对优先队列提出不同的要求。在进行需求收集时，首先要明确优先队列将被应用于什么样的业务场景中。比如说，如果优先队列用于一个订单处理系统，那么可能需要根据订单的紧急程度或者顾客等级进行优先级排序。一旦明确了业务场景，接下来就是进行需求的分类：

- **功能性需求**：这类需求通常关注优先队列需要实现的基本功能，例如插入、删除最小元素、更新元素优先级等。
- **性能性需求**：在性能方面的需求可能包括时间复杂度、空间复杂度、以及在高负载情况下的稳定性和可靠性等。
- **安全性需求**：尽管优先队列通常不涉及直接的安全性问题，但在某些应用场景中，可能需要考虑数据的完整性和防篡改特性。

### 3.1.2 需求优先级的确定方法

确定需求优先级的一个常用方法是通过MoSCoW方法：

- **Must have**：必须有的需求，没有这些功能系统无法正常工作。
- **Should have**：应该有的需求，这些是提高用户体验或系统性能的重要功能。
- **Could have**：可以有的需求，这些需求在有足够资源和时间的情况下可以考虑实现。
- **Won't have**：不打算有的需求，这些需求在目前的开发周期内不会被实现，可能是由于资源限制或优先级较低。

通过这样的方法，可以更加清晰地界定和排序需求，为后续的系统设计与实现提供指导。

## 3.2 自定义优先队列的设计原则

### 3.2.1 扩展性与灵活性

设计自定义优先队列时，我们需要考虑如何让这个结构在未来容易地添加新的特性。扩展性和灵活性是两个关键的设计原则。扩展性意味着系统能够在不影响原有功能的前提下增加新的功能。例如，可以在优先队列的基础上增加一个功能，用于追踪每个插入元素的原始优先级信息。

### 3.2.2 性能考量

性能是衡量数据结构好坏的关键指标。设计时应该关注如下几点：

- **时间复杂度**：操作插入、删除最小元素等关键操作的效率。
- **空间复杂度**：存储元素所占用的内存。
- **缓存友好性**：数据结构在内存中的布局应该尽量利用CPU缓存，以减少访问延迟。
- **并发性能**：对于多线程环境，如何高效地处理并发访问，避免死锁和其他并发问题。

## 3.3 自定义优先队列的场景实例

### 3.3.1 网络流量管理

在复杂的网络系统中，可能需要根据不同的数据包类型或者源地址来决定数据包的传输优先级。这时，网络流量管理系统会利用一个优先队列来安排数据包的处理顺序。在这个场景中，优先队列需要根据预定义的规则快速调整队列中的元素顺序，以保证高优先级的数据包被优先处理。

### 3.3.2 实时操作系统任务调度

在实时操作系统中，任务调度器根据任务的优先级来分配CPU资源。为了实现这一功能，操作系统会使用优先队列来管理这些任务。在这个场景下，任务可以动态地添加到队列中，并且根据优先级的变化被重新排序。这要求优先队列具备高效率的插入和删除操作，同时能够快速地找到并调度优先级最高的任务。

以上内容展现了自定义优先队列需求分析的深度和广度，下一章节将会深入到如何实现自定义优先队列的数据结构。

# 4. 实现自定义优先队列的数据结构

在本章节，我们将深入探讨如何实现自定义优先队列的数据结构。自定义