Python堆与优先队列应用：案例驱动的深入剖析

# 1. Python堆与优先队列概念解析

在计算机科学中，堆（Heap）是一种特殊的完全二叉树，用于实现优先队列（Priority Queue）。优先队列是一种抽象数据结构，每个元素都拥有一个优先级，具有最高优先级的元素总是第一个被删除。堆结构提供了一种高效的方式来管理和维护这样的数据集。

## 2.1 堆的基本概念和特性

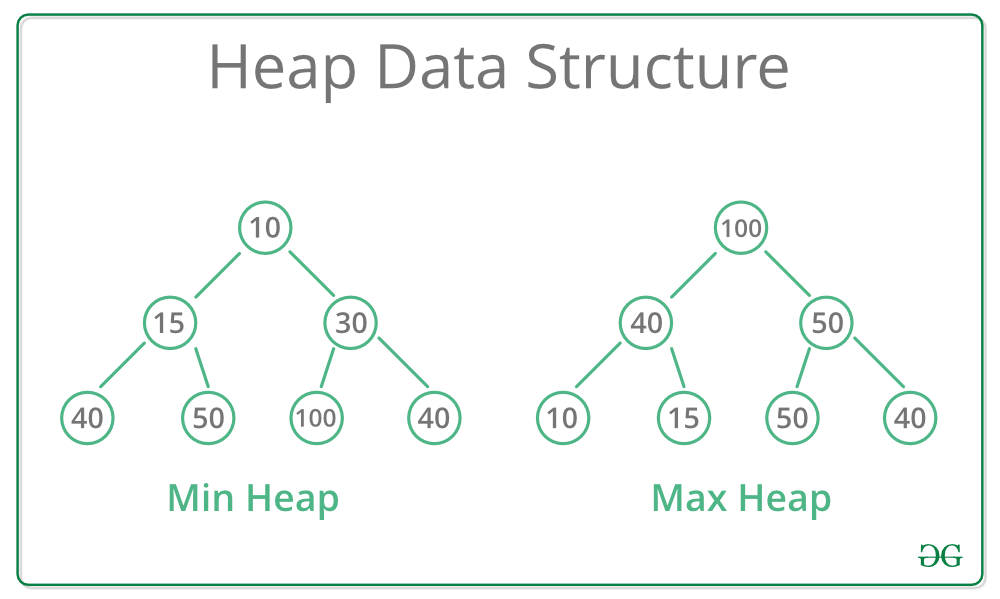
### 2.1.1 什么是堆

堆是一种特殊的二叉树，它满足堆性质：任何一个父节点的值都必须大于或等于（在最小堆中）或者小于或等于（在最大堆中）其子节点的值。这种结构特别适合实现优先队列，因为它可以快速找到最大或最小元素。

### 2.1.2 堆与优先队列的关系

堆是优先队列的一种实现方式。优先队列要求按照元素的优先级顺序来访问，堆结构的性质确保了根节点（队列的头部）始终是所有节点中优先级最高（或最低）的，因此能够支持快速的插入和删除操作。

## 2.2 堆的操作和实现细节

### 2.2.1 堆的插入和删除操作

堆的插入操作通常称为`push`，它将一个元素添加到堆的末尾，然后执行上浮（`heapify-up`）操作以恢复堆性质。删除操作通常称为`pop`，它移除并返回根节点，然后将堆的最后一个元素放到根的位置，并执行下沉（`heapify-down`）操作来重建堆。

### 2.2.2 堆的遍历和重建

堆的遍历通常指的是访问堆中所有元素的操作，由于堆通常用数组实现，因此可以按顺序访问数组的元素来实现遍历。堆的重建指的是在所有元素被删除后，如何通过一系列操作使一个空堆重新成为有效的堆结构。

在下一章节，我们将深入探讨堆结构的具体操作和实现细节，并通过示例代码来展示其在实际中的应用。

# 2. 堆结构的理论与实践

## 2.1 堆的基本概念和特性

### 2.1.1 什么是堆

堆是一种特殊的完全二叉树，满足任何父节点的值都大于或等于（在最小堆的情况下）其子节点的值。堆可以用于实现优先队列，并且在许多算法中作为数据结构来维持最大或最小元素。堆通常通过数组来实现，因为它们允许通过简单的索引计算访问任何节点的父节点或子节点，这对于快速插入和删除操作至关重要。

### 2.1.2 堆与优先队列的关系

优先队列是一种抽象数据类型，其中的元素都有各自的优先级，并且优先级最高的元素总是被首先删除。堆是实现优先队列的一种有效方式，因为它可以快速定位到优先级最高的元素，并支持快速的插入和删除操作。在Python中，我们可以使用内置的`heapq`模块来利用堆这种数据结构。

## 2.2 堆的操作和实现细节

### 2.2.1 堆的插入和删除操作

插入操作涉及将元素添加到堆的末尾，并通过上浮（sift up）操作来维护堆的性质。上浮操作通过比较新添加的元素与其父节点，如果新元素的优先级更高，则与父节点交换位置，直到堆的性质得到恢复。

删除操作通常指的是删除堆的根节点，即优先级最高的元素。这可以通过将堆的最后一个元素移动到根位置并删除最后一个元素，然后通过下沉（sift down）操作来维护堆的性质来完成。下沉操作会比较父节点与其子节点的值，并将较大的子节点与父节点交换，直到达到叶子节点。

### 2.2.2 堆的遍历和重建

堆的遍历通常指的就是按层遍历，它遵循完全二叉树的特性。遍历得到的序列与数组中的顺序是一致的，这是由于堆的物理表示就是基于数组的。

当堆的结构被破坏时，比如通过替换某些元素，我们需要通过“重建堆”的过程来恢复堆的性质。这可以通过从最后一个非叶子节点开始，执行下沉操作直到根节点来实现。

## 2.3 堆的算法应用

### 2.3.1 堆排序算法

堆排序算法利用堆的特性来对元素进行排序。它包含两个主要的步骤：建立堆结构和逐步取出堆顶元素。在堆结构建立起来之后，可以持续地将堆顶元素（最大或最小值）与堆的最后一个元素交换，并减少堆的大小，然后执行下沉操作以恢复堆的性质。重复这个过程，直到堆的大小缩减到1，此时数组就会被排序。

### 2.3.2 堆在图算法中的应用

堆在图算法中也有广泛的应用，特别是在Dijkstra的最短路径算法和Prim的最小生成树算法中。在Dijkstra算法中，堆用于存储待处理的节点，并允许算法以最小距离的节点作为下一个处理目标，从而有效地减少需要处理的节点数量。在Prim算法中，堆帮助算法快速找到连接当前生成树与剩余顶点中权重最小的边。

下一章节将继续深入堆与优先队列的内部机制，为读者提供更深入的理解和实际应用。

# 3. 优先队列的理论与实践

在数据结构领域，优先队列是一种特殊的队列，它的元素具有优先级属性，能够保证每次从队列中取出的都是优先级最高的元素。不同于普通队列先进先出的特性，优先队列支持更复杂的操作，使得其在许多算法和系统中有着广泛的应用。本章节深入探讨优先队列的基本概念、操作实现细节以及算法应用，并通过实例来展示其在实际问题中的应用场景。

## 3.1 优先队列的基本概念和特性

### 3.1.1 优先队列的定义和作用
优先队列(Priority Queue)是具有优先级属性的元素集合，每个元素都有一个优先级值。在优先队列中，元素的出队顺序是由优先级决定的，优先级最高的元素将会优先出队。

**定义**: 优先队列是一个动态数据集合，可以看作是带有优先级的队列，支持插入和删除最小元素的操作。优先队列的典型应用场景包括任务调度、事件驱动模拟等。

**作用**: 优先队列的作用在于能够高效地管理具有不同优先级的任务或数据。例如，在任务调度系统中，可以将任务的紧急程度作为优先级，确保最关键的任务得到优先处理。

### 3.1.2 优先队列与堆的关系
优先队列的内部实现经常依赖于堆这种数据结构，尤其是二叉堆(binary heap)。堆提供了一种方便的方式来维持优先队列中元素的有序性，使得插入和删除最小元素的操作可以高效地完成。

堆是一种特殊的完全二叉树，它满足堆性质：任何一个父节点的值都必须大于（或小于）其子节点的值。二叉堆的两种主要形式是最大堆（父节点的值总是大于子节点的值）和最小堆（父节点的值总是小于子节点的值）。由于最小堆可以高效地实现优先队列的操作，因此通常在优先队列的实现中使用。

## 3.2 优先队列的操作和实现细节

### 3.2.1 优先队列的插入和删除操作
优先队列支持两种基本操作：插入新元素（push）和删除具有最高优先级的元素（pop）。

**插入操作（push）**: 将一个新元素添加到优先队列中，随后调整堆结构以维持堆性质。插入操作的复杂度通常为O(log n)，其中n是队列中的元素数量。

**删除操作（pop）**: 从优先队列中删除具有最高优先级的元素（即最小堆的根节点或最大堆的根节点），然后将最后一个元素移动到根节点的位置，再通过堆调整