图算法在Python中的实践：源码与应用场景深度分析

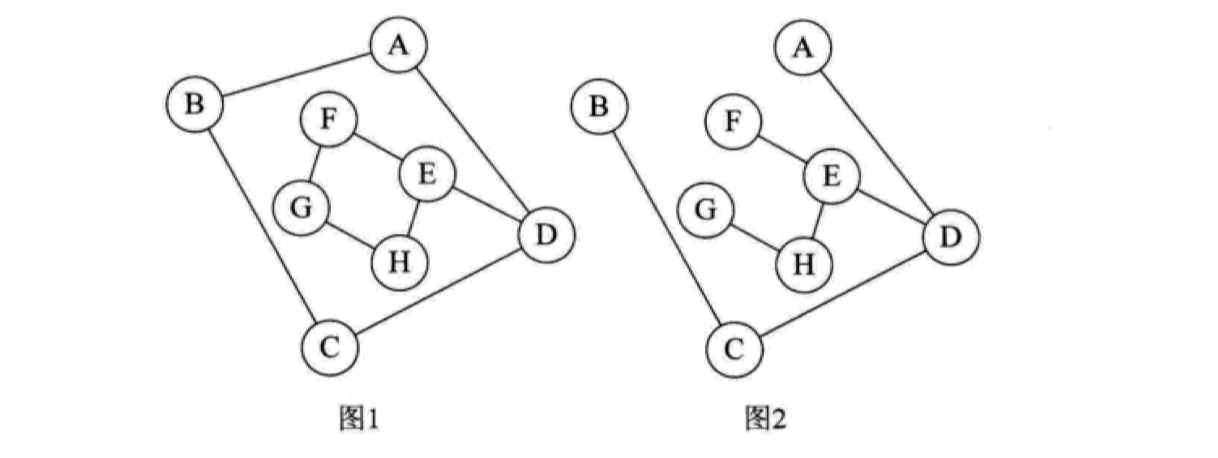
# 1. 图算法基础概念与术语

## 1.1 图的定义
图是数学中的一种基础结构，它由顶点（节点）的有穷非空集合和顶点之间边的集合组成。顶点通常用V表示，边用E表示。形式上，图G可以定义为G=(V,E)。图的种类很多，包括无向图、有向图、带权图等。在计算机科学中，图用于模拟各种网络结构和复杂关系。

## 1.2 关键术语介绍
在图论中，有几个核心术语需要熟悉：
- **邻接（Adjacency）**：若两个顶点间存在边，则称它们是邻接的。
- **路径（Path）**：路径是顶点序列，序列中的顶点是依次相邻的。
- **环（Cycle）**：路径的起始顶点和结束顶点相同的路径称为环。
- **连通性（Connectivity）**：在无向图中，如果两个顶点间存在路径，则称这两个顶点是连通的。
- **强连通与弱连通**：在有向图中，需要区分强连通（双向路径）和弱连通（仅存在单向路径）。

## 1.3 图的表示方法
图可以用多种方法表示，主要包括：
- **邻接矩阵**：一个n×n的矩阵，其中每个元素表示顶点间的关系，通常是0或1，表示无连接或有连接。
- **邻接表**：一个由顶点列表组成的数据结构，每个顶点的列表包含其所有邻接顶点。

图的数据结构设计及其在算法中的应用是图算法研究的基础，理解了这些概念，我们就为更深入地探讨图算法及其应用奠定了坚实的基础。在后续章节中，我们将学习图在Python中的实现，以及图算法的实际应用案例。

# 2. Python中的图数据结构实现

## 2.1 Python内置数据结构与图的关系

### 2.1.1 字典和集合在图中的应用

在Python中，字典和集合是两种非常灵活且强大的内置数据结构。它们在实现图算法时扮演着关键角色，特别是在表示图的数据结构时。

字典通常用于实现邻接表，每个键对应一个节点，而其值则是一个集合，表示与该节点相连的所有节点。这种结构不仅节省内存，还便于管理图中的边。

# 使用字典和集合创建一个无向图的例子
graph = {
    'A': {'B', 'C'},  # 节点A连接的节点集合
    'B': {'A', 'D', 'E'},  # 节点B连接的节点集合
    'C': {'A', 'F'},  # 节点C连接的节点集合
    'D': {'B'},  # 节点D连接的节点集合
    'E': {'B', 'F'},  # 节点E连接的节点集合
    'F': {'C', 'E'}  # 节点F连接的节点集合
}

### 2.1.2 列表和元组在图算法中的角色

列表和元组通常用于表示图中的边。在Python中，可以使用列表存储边，其中每个元素是一个包含两个节点标识符的元组，表示一条边。元组的不可变性保证了边的唯一性。

# 使用列表和元组创建一个有向图的例子
edges = [
    ('A', 'B'),
    ('A', 'C'),
    ('B', 'D'),
    ('C', 'F'),
    ('D', 'B'),
    ('F', 'E')
]

# 从边列表构建邻接表字典
adjacency_list = {}
for edge in edges:
    if edge[0] not in adjacency_list:
        adjacency_list[edge[0]] = set()
    adjacency_list[edge[0]].add(edge[1])

## 2.2 使用邻接表和邻接矩阵

### 2.2.1 邻接表的设计和实现

邻接表是一种将图中的每条边表示为一对节点的数据结构，通常采用字典实现，键为起始节点，值为与起始节点相连的节点集。邻接表非常适合表示稀疏图，并且能够快速完成图的遍历操作。

邻接表的设计需要考虑图的类型（有向或无向）、边的权重等因素。在有向图中，节点A到节点B的连接并不意味着节点B到节点A也存在连接；而在无向图中，节点A到节点B的连接同时意味着节点B到节点A的连接。

# 一个简单的邻接表实现
class Graph:
    def __init__(self):
        self.adjacency_list = {}

    def add_vertex(self, vertex):
        if vertex not in self.adjacency_list:
            self.adjacency_list[vertex] = set()

    def add_edge(self, source, destination):
        if source in self.adjacency_list:
            self.adjacency_list[source].add(destination)
        else:
            print("Source vertex not found in the graph")

# 使用示例
g = Graph()
g.add_vertex('A')
g.add_vertex('B')
g.add_edge('A', 'B')

### 2.2.2 邻接矩阵的特性及应用

邻接矩阵是一个二维数组，其中的行和列分别对应图中的各个节点，矩阵中的元素表示节点之间的连接关系。对于无向图，邻接矩阵是对称的；对于有向图，则可能不对称。邻接矩阵非常适合表示稠密图。

邻接矩阵的一个优点是可以通过简单的索引操作快速检查两个节点之间是否存在边，无需额外的存储空间来存储节点之间的连接信息。然而，对于稀疏图，邻接矩阵可能非常浪费空间，因为每个节点对都需要一个矩阵元素，无论它们之间是否存在边。

# 邻接矩阵的简单实现
class GraphMatrix:
    def __init__(self, size):
        self.matrix = [[0 for _ in range(size)] for _ in range(size)]

    def add_edge(self, row, col):
        self.matrix[row][col] = 1
        if row != col:  # 无向图的邻接矩阵是对称的
            self.matrix[col][row] = 1

# 使用示例
g = GraphMatrix(4)
g.add_edge(0, 1)
g.add_edge(1, 2)

## 2.3 图的常见操作和算法

### 2.3.1 图的遍历算法

图的遍历算法是探索图中所有顶点并访问每个顶点一次的过程。根据图的类型（有向或无向）、边的权重以及遍历的起始点，存在两种基本的遍历算法：深度优先搜索（DFS）和广度优先搜索（BFS）。这两种算法在查找图中的路径、检测环、拓扑排序以及解决许多其他问题时非常有用。

- **深度优先搜索（DFS）**：按照可能的分支路径深入直到某节点不可达为止，然后再回溯到前一个节点并探索另一条路径。
- **广度优先搜索（BFS）**：从一个节点开始，先访问其所有相邻节点，然后对每一个相邻节点，再访问它们的未被访问的相邻节点。

# DFS和BFS算法实现示例代码
from collections import deque

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start, end=' ')
    for next_node in graph[start]:
        if next_node not in visited:
            dfs(graph, next_node, visited)
    return visited

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node, end=' ')
            visited.add(node)
            queue.extend(set(graph[node]) - visited)
    return visited

# 有向图
graph = {
    'A': {'B', 'C'},
    'B': {'D', 'E'},
    'C': {'F'},
    'D': {},
    'E': {'F'},
    'F': {}
}

print("DFS traversal:")
dfs(graph, 'A')
print("\nBFS traversal:")
bfs(graph, 'A')

### 2.3.2 最短路径和最小生成树算法

在图算法中，寻找最短路径和最小生成树是两类常见的问题。最短路径问题关注的是找到图中两个节点之间路径的最短长度，而最小生成树问题则是在无向加权图中找到连接所有节点且总权重最小的树。

- **最短路径问题**：最常用的算法是迪杰斯特拉（Dijkstra）算法，适用于没有负权边的图。另一个著名的算法是弗洛伊德（Floyd-Warshall）算法，它能够解决所有顶点之间的最短路径问题。
- **最小生成树问题**：常见的算法有普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。Prim算法从某一顶点开始，逐步添加边和顶点到最小生成树中；而Kruskal算法则按照边的权重顺序，将边添加到最小生成树中。

import heapq

def dijkstra(graph, start):
    distances =