【Python算法挑战攻略】：解决LeetCode算法难题

# 1. Python算法挑战攻略导言

## 引言
在这个信息爆炸的时代，算法作为IT技术的核心之一，不仅在编程竞赛中占据着举足轻重的地位，更是软件开发、数据科学与人工智能等领域必备的技能。掌握算法，意味着拥有解决问题的能力，而Python凭借其简洁、易读的特点，成为了学习算法的首选语言。本文旨在通过系统性的攻略，帮助读者克服Python算法挑战，无论你是算法新手还是寻求提升的老手，都能在此找到进步的方向和方法。

## 目标人群定位
文章的目标读者是有志于提升自己算法技能的IT从业者，特别是那些对Python语言有一定了解、希望深入学习算法的中级及以上水平的读者。通过逐步深入的内容，读者不仅能巩固基础知识，还能掌握实用的算法技巧，为参加算法竞赛、职场面试等做好充分准备。

## 章节概览
从本文目录可以看出，我们将从基础知识回顾开始，到具体的算法实践，再到深入理解算法难题，并在最后提供算法竞赛与职业准备的策略。内容层层递进，不仅涵盖了理论知识，更强调了实战应用和问题解决技巧。

这篇文章的第一章就为读者们提供了一个全面的Python算法挑战攻略的概览，接下来的章节将进一步深入解析，每一步都旨在为读者提供系统性的学习路径和实用的解决问题的方法。

# 2. Python基础知识回顾

Python作为一种高级编程语言，在IT行业的应用非常广泛。它以其简洁的语法、强大的库支持和高效的开发特性成为了开发者的首选之一。在开始研究复杂的算法挑战之前，有必要对Python的基础知识进行一个全面的回顾。本章将涵盖数据结构、算法理论基础以及函数式编程这三个主要领域，为后续章节的深入探讨打下坚实的基础。

## 2.1 数据结构基础

### 2.1.1 列表、元组和字典的使用

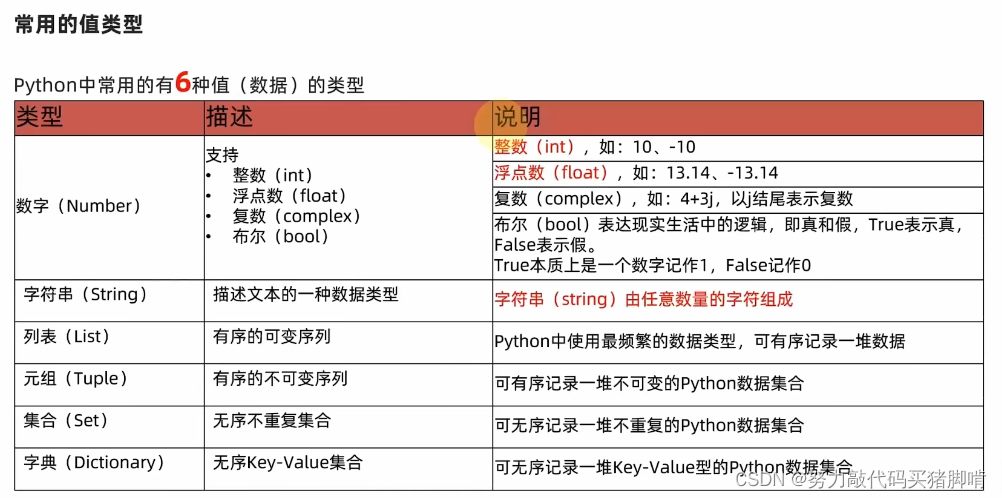
在Python中，列表（list）、元组（tuple）和字典（dictionary）是最常用的数据结构。理解它们的特性及其应用场景对于编写高效代码至关重要。

- 列表是一种有序的集合，可以随时添加和删除其中的元素。它使用方括号[]定义，并且可以包含任意类型的对象。
- 元组与列表类似，但是元组一旦创建就不能被修改，即它是不可变的。元组使用圆括号()定义。
- 字典是一种映射类型，它存储的是键值对（key-value pairs），且每个键都是唯一的。字典使用花括号{}定义，并通过键来存取对应的值。

在实际应用中，列表经常用于存储和操作序列数据，元组用于确保数据不变性，而字典则常用于实现快速查找和存储关联信息。

#### 示例代码块

# 列表的创建和操作
fruits = ['apple', 'banana', 'cherry']
fruits.append('orange')  # 添加元素
print(fruits[1])         # 访问元素
del fruits[0]            # 删除元素

# 元组的创建和特性
point = (10, 20)
print(point[0])          # 访问元组中的元素
# point[0] = 30          # 错误：元组是不可变的

# 字典的创建和使用
person = {'name': 'Alice', 'age': 25}
print(person['name'])    # 访问字典中的值
person['age'] = 26       # 更新字典中的值

### 2.1.2 字符串和集合的操作技巧

Python中的字符串和集合也是两种重要的数据结构。

- 字符串是字符的有序集合，可以使用单引号(')、双引号(")或三引号('''或""")定义。
- 集合（set）是一个无序的不重复元素序列，可以使用花括号{}定义或set()函数创建。

字符串和集合在数据处理和操作中扮演着重要角色，尤其是当需要处理文本数据或进行集合运算时。

#### 示例代码块

# 字符串的创建和操作
greeting = "Hello, World!"
print(greeting.upper())  # 转换为大写
print(greeting.split(','))  # 分割字符串

# 集合的创建和操作
fruits_set = {'apple', 'banana', 'cherry'}
fruits_set.add('orange')  # 添加元素
print(fruits_set.remove('banana'))  # 删除元素

## 2.2 算法理论基础

### 2.2.1 时间复杂度和空间复杂度分析

在算法领域，时间复杂度和空间复杂度是衡量算法性能的两个重要指标。理解这两个概念对于设计和优化算法至关重要。

- 时间复杂度是衡量算法运行时间的一个度量，它关注的是随着输入数据的增长，算法执行时间的增长趋势。
- 空间复杂度则是衡量算法所需存储空间的增长趋势。

一般来说，我们使用大O符号（O-notation）来描述复杂度，常见的复杂度从低到高排序大致为：O(1), O(log n), O(n), O(n log n), O(n^2), O(2^n), O(n!)。

#### 示例代码块

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

# 线性搜索的时间复杂度分析
# 该函数的最坏情况下的时间复杂度为 O(n)，
# 其中 n 是列表 arr 的长度。

### 2.2.2 常见算法概念与原理

在算法学习的过程中，掌握常见的算法概念和原理是非常重要的。这包括但不限于排序、搜索、递归、动态规划等。

- 排序算法如冒泡排序、选择排序、插入排序、快速排序等，它们在数据预处理阶段至关重要。
- 搜索算法如线性搜索和二分搜索，在数据查找场景中非常实用。
- 递归是一种常见的编程技巧，它允许函数调用自身。递归是许多复杂算法如树和图遍历的基础。
- 动态规划是一种通过将问题分解为重叠子问题，并以某种方式存储这些子问题的解决方案的技巧，从而避免重复计算，优化算法效率。

#### 示例代码块

# 快速排序算法原理的简要概述
def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

# 快速排序的时间复杂度分析
# 平均情况下，该算法的时间复杂度为 O(n log n)，但在最坏的情况下会退化到 O(n^2)。

## 2.3 Python中的函数式编程

### 2.3.1 高阶函数和装饰器

Python支持函数式编程，它提供了一些在函数中传递函数、返回函数和将函数作为参数的特性。

- 高阶函数是至少满足下列一个条件的函数：接收一个或多个函数作为输入，或输出一个函数。
- 装饰器是一种特殊类型的高阶函数，它允许在不修改被调用函数代码的情况下增加函数的额外功能。

装饰器在日志记录、性能测试、事务处理等场景中非常有用。

#### 示例代码块

# 高阶函数示例：map()
def square(x):
    return x * x

numbers = [1, 2, 3, 4, 5]
squared_numbers = map(square, numbers)
print(list(squared_numbers))

# 装饰器示例：日志装饰器
def log_decorator(func):
    def wrapper(*args, **kwargs):
        print(f"Calling {func.__name__} with arguments {args} and keyword arguments {kwargs}")
        result = func(*args, **kwargs)
        print(f"{func.__name__} returned {result}")
        return result
    ret