环境科学数据分析:MATLAB统计工具箱应用与案例分析
发布时间: 2024-12-09 22:12:26 阅读量: 3 订阅数: 19 

# 1. MATLAB统计工具箱概览
MATLAB统计工具箱是针对数据分析和统计建模的专业工具集,它为用户提供了强大的统计分析功能。该工具箱集成了多种统计学方法和算法,从基础的数据分析到高级的模型拟合,应有尽有,极大地提高了数据分析的效率和准确性。
## 1.1 工具箱特点
统计工具箱具有操作简单、功能全面的特点。它不仅支持传统的统计分析方法,还集成了机器学习和深度学习模型,使得在数据分析过程中能够实现更深层次的洞察。
## 1.2 工具箱应用范围
该工具箱广泛应用于金融分析、生物统计、环境科学、工程计算等多个领域。通过使用MATLAB统计工具箱,研究人员和工程师能够快速实现数据探索、预测分析和结果解释。
## 1.3 入门基础
对于初学者,建议先从数据的导入导出、基本统计量的计算开始,逐步掌握更多高级功能。官方文档和示例脚本是学习的好帮手,同时社区论坛和培训课程也是深化理解的途径。
```matlab
% 示例代码:导入数据并计算均值
data = load('example_data.csv'); % 加载CSV文件数据
mean_value = mean(data); % 计算数据的均值
disp(['The mean value is ', num2str(mean_value)]);
```
上述示例代码展示了如何在MATLAB中执行基本的数据操作。随后的章节将进一步深入介绍MATLAB统计工具箱的功能和应用。
# 2. MATLAB统计基础与理论
### 2.1 统计学基础
#### 2.1.1 数据类型和统计量
在统计学中,数据类型可以大致分为两类:定量数据和定性数据。定量数据通常是连续的,可以进行精确测量和算术运算,例如身高的厘米数或者温度的摄氏度。定性数据则是分类的,用于标识物体或事件的种类或属性,例如性别或者血型。
统计量是对数据集的某个特征进行量化的度量,常见的统计量包括:
- **均值**:所有数据值的总和除以数据的数量。它反映了数据集的中心位置。
- **中位数**:将数据集从小到大排序后位于中间位置的值。它对极端值不敏感,能更好地反映数据集的整体趋势。
- **众数**:数据集中出现次数最多的值。它反映了数据集的典型值。
- **方差**:衡量数据值与均值之间的偏差大小。它提供了数据集分散程度的一个度量。
- **标准差**:方差的平方根。由于单位与原始数据相同,因此更易于解释。
#### 2.1.2 常见统计分布
在统计分析中,某些特定的分布形式被频繁使用,如:
- **正态分布**:对称的钟形曲线,其均值、中位数和众数相同,大多数观测值集中在均值附近。
- **二项分布**:描述了在固定次数的独立实验中,成功的次数的概率分布,实验结果仅限于成功或失败。
- **泊松分布**:描述在固定时间或空间间隔内,事件发生次数的概率分布。
### 2.2 数据处理与分析方法
#### 2.2.1 数据清洗和预处理
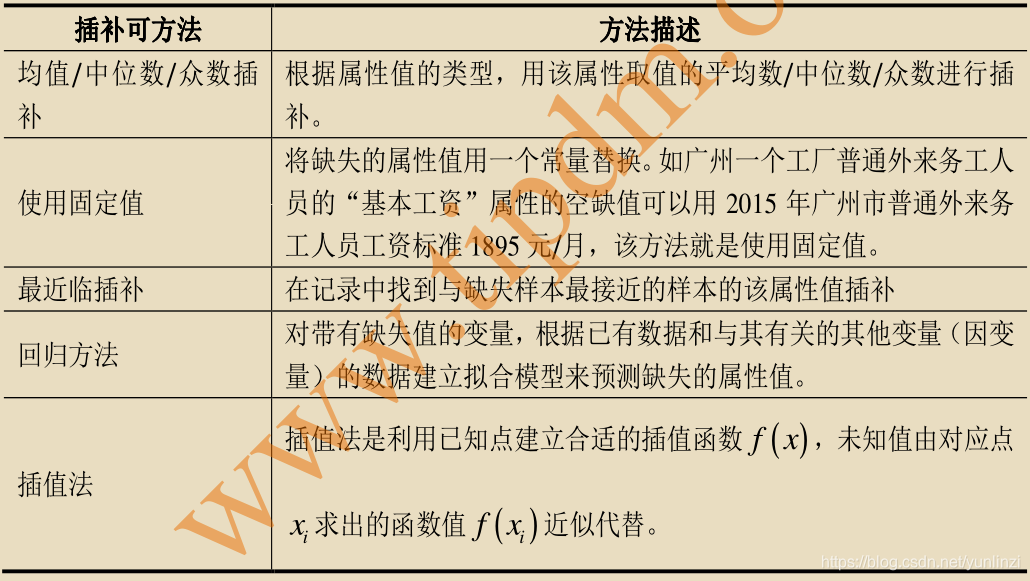
在进行统计分析之前,数据清洗和预处理是关键的步骤。这个过程包括:
- **处理缺失值**:通过删除缺失数据或使用算法估计缺失值来处理。
- **去除异常值**:异常值可能是由于测量错误或自然变化导致的,需要适当的方法来识别和处理。
- **数据归一化**:将数据缩放到一个标准范围,消除不同量纲对分析结果的影响。
#### 2.2.2 基本统计分析方法
基本统计分析方法包括描述性统计和推断性统计。
- **描述性统计**:通过计算均值、中位数、众数、方差等统计量来概括数据集的主要特征。
- **推断性统计**:使用样本数据来推断总体参数,如置信区间估计和假设检验。
### 2.3 MATLAB中的统计函数
#### 2.3.1 数据描述函数
MATLAB提供了许多用于数据描述的函数,例如:
```matlab
data = [1, 2, 3, 4, 5]; % 示例数据集
meanValue = mean(data); % 计算均值
medianValue = median(data); % 计算中位数
modeValue = mode(data); % 计算众数
varianceValue = var(data); % 计算方差
stdValue = std(data); % 计算标准差
```
这些函数可以直接应用在数据集上,以获得相关的统计描述。
#### 2.3.2 假设检验与置信区间函数
假设检验和置信区间是推断性统计的重要组成部分。MATLAB提供了如下函数:
```matlab
tStat = ttest(data, 3); % 单样本t检验,假设均值为3
[pValue, ci] = tconfint(data); % 计算均值的95%置信区间
```
这些函数允许用户对数据集进行更深入的统计分析。
以上章节内容中,我们介绍了统计学的基础概念、数据类型、常见统计分布、数据处理和分析方法以及MATLAB中对应的统计函数。这些基础知识为后续章节中涉及的统计工具箱高级应用打下了坚实的基础。在下一章节中,我们将深入探讨MATLAB统计工具箱在多变量数据分析、时间序列分析和构建高级统计模型方面的应用。
# 3. MATLAB统计工具箱高级应用
随着数据分析的深入,MATLAB统计工具箱提供了更多的高级功能以应对复杂的统计需求。这些功能可以帮助用户从多角度深入挖掘数据,发现数据之间的潜在关联,预测未来的数据走向,并且构建复杂的统计模型。
## 3.1 多变量数据分析
多变量数据分析涉及同时处理和分析两个或两个以上的变量。这允许用户探索变量间的相互关系、数据结构及变量对整体数据集的影响。以下是MATLAB中多变量数据分析的两种常用技术。
### 3.1.1 主成分分析(PCA)
主成分分析(PCA)是一种统计方法,通过正交变换将一组可能相关的变量转换为一组线性不相关的变量,这些新变量称为主成分。使用PCA可以简化数据,同时尽可能地保留原始数据的信息。
在MATLAB中使用PCA的步骤包括:
- 数据的中心化和标准化(如果需要)
- 计算协方差矩阵
- 通过协方差矩阵求解特征值和特征向量
- 选择主成分并构建降维后的数据
```matlab
% 假设data是一个m×n的矩阵,其中m是观测数,n是变量数
data = ...; % 加载或生成数据矩阵
% 中心化数据
data_centered = data - mean(data, 1);
% 计算协方差矩阵
cov_matrix = cov(data_centered);
% 计算特征值和特征向量
[V, D] = eig(cov_matrix);
% 特征值排序,以选择主成分
[V_sorted, ind] = sort(diag(D), 'descend');
V = V(:, ind);
% 构建降维后的数据
num_components = 2; % 假设我们选择两个主成分
data_pca = data_centered * V(:, 1:num_components);
% 可视化结果
scatter(data_pca(:,1), data_pca(:,2));
```
在这段代码中,首先对数据进行了中心化处理,然后求解了协方差矩阵。接着,计算特征值和特征向量,并将特征值按从大到小排序。最后,选择前两个特征向量作为主成分,并将原数据投影到这两个主成分形成的低维空间。
### 3.1.2 因子分析
因子分析是一种降维技术,它假设一组观测变量是由一组无法直接观测的潜在变量(因子)共同影响的结果。它旨在寻找变量背后的结构,即发现变量共享的公共因子。
MATLAB中的因子分析步骤可能包括:
- 对数据进行标准化处理
- 估计变量间的相关系数矩阵
- 提取因子并进行因子旋转
- 通过因子得分矩阵解释因子
```matlab
% 假设standardized_data是一个标准化后的数据矩阵
standardized_data = ...; % 加载或生成标准化数据
% 估计相关系数矩阵
correlation_matrix = corr(standardized_
```
0
0





