JavaFX布局优化：Fxml提升效率的秘诀

# 1. JavaFX布局概述与Fxml入门

## 1.1 JavaFX布局简介
JavaFX 提供了丰富的UI组件和布局管理器，以帮助开发者构建动态、响应式的图形用户界面。布局管理器允许以一致和有效的方式管理控件在界面中的位置和大小。

## 1.2 Fxml的引入
为了更高效地设计复杂用户界面，JavaFX引入了Fxml，这是一种基于XML的标记语言，用于描述UI组件和它们的布局。Fxml的使用使得UI设计与Java代码逻辑分离，从而使界面设计工作可以由设计人员独立完成。

## 1.3 Fxml的优势
使用Fxml的优势在于它提高了代码的可读性和可维护性，允许开发人员通过声明性的方式构建布局，这有助于简化代码结构，并允许布局的重用和模块化。

<!-- 示例：Fxml文件中的简单布局 -->
<?xml version="1.0" encoding="UTF-8"?>
<?import javafx.scene.layout.*?>
<?import javafx.scene.control.*?>

<GridPane xmlns:fx="***" fx:controller="com.example.Controller"
          alignment="center" hgap="10" vgap="10">
    <Button text="Click Me!" onAction="#handleButtonAction" GridPane.columnIndex="1" GridPane.rowIndex="1"/>
</GridPane>

以上是一个Fxml文件的简单示例，它展示了如何在GridPane布局中添加一个按钮，并通过`onAction`属性将点击事件与后端Java代码中的方法绑定。这表明Fxml的使用能够使UI布局和事件处理结构化且易于理解。

在下一章节中，我们将深入探讨Fxml布局的组成元素以及如何组织控件和设置布局属性。

# 2. 深入理解Fxml布局结构

## 2.1 Fxml布局基础

### 2.1.1 Fxml的组成元素

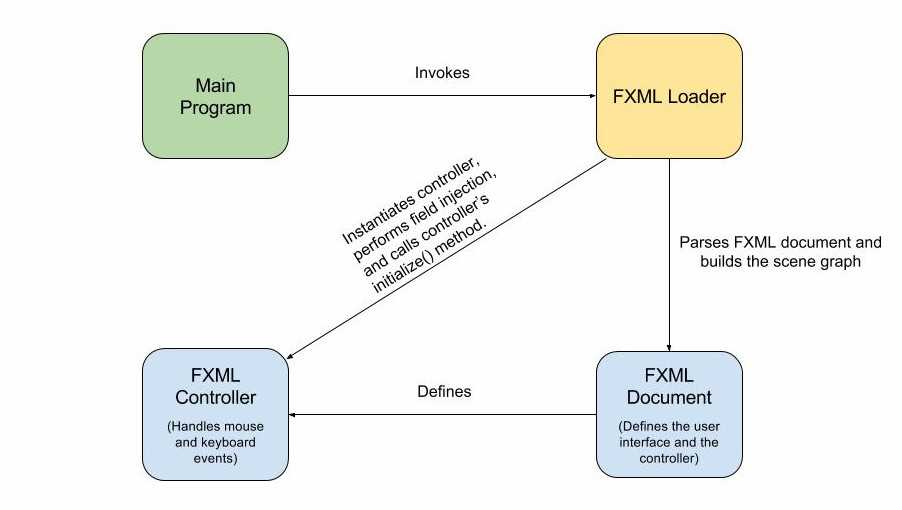
Fxml（FX Markup Language）是一种基于XML的标记语言，用于定义JavaFX应用程序的用户界面。Fxml文件包含一系列的组件元素，这些元素被用来创建和组织用户界面。最基本的Fxml文件包括场景（Scene）、舞台（Stage）、控制器（Controller）以及各种UI控件。

**场景（Scene）** 是应用程序用户界面的基本容器，一个场景可以包含一个或多个根节点，这些根节点可以是布局控件或者UI组件。

**舞台（Stage）** 是JavaFX应用程序的顶级窗口容器，每个应用程序只能有一个舞台。它作为容纳场景的容器，是应用程序显示给用户的地方。

**控制器（Controller）** 是一种特殊的类，通过使用`@FXML`注解可以与Fxml文件中的UI元素关联起来，从而实现逻辑代码与界面代码的分离。控制器类通常负责处理用户输入和更新界面。

### 2.1.2 控件的组织与布局属性

在Fxml中定义的每个控件，都可以拥有多个布局属性，这些属性决定了控件在布局中的位置、大小以及显示样式。常用的布局属性包括：

- `GridPane` 控件可以使用`gridRow`和`gridColumn`属性来指定放置在网格的哪一行和哪一列。
- `AnchorPane` 使用`topAnchor`, `bottomAnchor`, `leftAnchor`, `rightAnchor` 属性来将控件锚定到布局的边缘。
- `Region` 类的 `padding` 属性用于控制控件的边距，`prefWidth` 和 `prefHeight` 属性用于设置控件的首选宽度和高度。
- `alignment` 属性在很多布局控件中都非常有用，它用于控制子节点的对齐方式。

<AnchorPane xmlns:fx="***" fx:controller="com.example.Controller">
    <Button text="Button" layoutX="50" layoutY="50" anchorX="25" anchorY="15"/>
    <!-- 其他控件 -->
</AnchorPane>

## 2.2 高级布局技巧

### 2.2.1 使用GridPane和AnchorPane

`GridPane` 和 `AnchorPane` 是构建复杂布局时不可或缺的两个布局控件。`GridPane` 提供了一个基于网格的布局，可以很方便地创建表格形式的布局。通过定义行和列，可以将不同的控件放置在不同的网格单元中。

<GridPane>
    <Button text="One" GridPane.rowIndex="0" GridPane.columnIndex="0"/>
    <Button text="Two" GridPane.rowIndex="0" GridPane.columnIndex="1"/>
    <!-- 其他按钮 -->
</GridPane>

另一方面，`AnchorPane` 允许我们通过锚点的方式将控件固定在布局的边缘或者相对位置。这种布局方式在需要控件在窗口大小调整时保持相对位置不变的情况下非常实用。

<AnchorPane>
    <Button text="Top Left" fx:id="topLeftButton" ***Anchor="10" AnchorPane.leftAnchor="10"/>
    <Button text="Bottom Right" AnchorPane.bottomAnchor="10" AnchorPane.rightAnchor="10"/>
</AnchorPane>

### 2.2.2 融合StackPane和Region创建复杂布局

`StackPane` 是一个将所有子节点叠放在一起的布局控件，可以用来覆盖图片或形状等在其他节点之上。而 `Region` 是所有布局和控件的基类，因此它具有一些通用的属性。我们可以利用这些特性来构建复杂的布局。

例如，可以将 `StackPane` 嵌套到 `Region` 的子控件中，实现多层叠放的效果：

<Region>
    <StackPane>
        <Circle fill="RED" radius="50"/>
        <Text text="Red Circle"/>
    </StackPane>
    <StackPane>
        <Circle fill="BLUE" radius="50"/>
        <Text text="Blue Circle"/>
    </StackPane>
</Region>

## 2.3 Fxml的事件处理和数据绑定

### 2.3.1 事件绑定机制

在 Fxml 中，事件处理通常是通过与控制器类中的方法绑定来实现的。我们可以通过 `fx:id` 属性为每个UI控件分配一个唯一的标识符，并在控制器类中使用`@FXML`注解来引用这些控件。然后，我们可以使用`setOnAction`方法或者在Fxml中使用`onAction`属性来为按钮等事件源添加事件处理器。

下面是一个示例，展示了如何在Fxml和控制器中处理按钮点击事件：

<Button fx:id="theButton" text="Click Me" onAction="#handleClick"/>

@Controller
public class MyController {
    @FXML
    private Button theButton;

    public void handleClick(ActionEvent event) {
        System.out.println("Button clicked!");
    }
}

### 2.3.2 数据绑定提升响应式UI

JavaFX 提供了强大的数据绑定机制，允许UI组件自动更新其显示的数据。在 Fxml 中，我们可以使用双大括号`{{ }}`来实现数据绑定。这个语法实际上是访问了JavaFX `Bindings`类中的静态方法，如`Bindings.capitalize`或者`Bindings.format`。

例如，我们可以将一个文本框的文本属性与一个字符串变量绑定：

<Text text="{{myStringProperty}}"/>

然后，在控制器中我们可以这样定义这个属性：

private StringProperty myStringProperty = new SimpleStringProperty("Initial Value");

public String getMyStringProperty() {
    return myStringProperty.get();
}

public void setMyStringProperty(String myString) {
    myStringProperty.set(myString);
}

通过这种绑定方式，当`myStringProperty`的值发生变化时，文本框中显示的值也会自动更新，从而提升UI的响应性和实时性。

# 3. Fxml布局性能优化实践

## 3.1 优化Fxml结构

### 3.1.1 减少层级和冗余控件

Fxml文件中的层级结构对应用性能有很大影响。层级越深，渲染速度可能会越慢，同时也会增加维护难度。为了优化性能，我们需要对Fxml结构进行审查和重构，减少不必要的嵌套层级。

减少层级的方法包括：
- 重新评估控件的组织方式，尝试将相似功能的控件合并。
- 移除多余的容器控件。如果一个控件内只包含一个子控件，这个容器控件就可以省略。
- 使用`fx:include`标签来代替嵌套的Fxml文件，这样可以保持控件结构扁平化，同时便于单独管理各个部分。

<!-- 示例：使用fx:include优化嵌套Fxml结构 -->
<FxmlRoot>
  <children>
    <!-- 其他控件 -->
    <fx:include source="path/to/otherPart.fxml"/>
  </children>
</FxmlRoot>

在这个示例中，`fx:include`标签被用来引入另一个Fxml文件，这样可以避免将整个文件的内容嵌套到当前文件中，从而减少层级。

### 3.1.2 使用样式表统一管理

为了提升性能，Fxml布局中样式属性的管理应优先考虑使用外部CSS样式表。通过使用样式表，我们可以对多个控件应用一组样式规则，这样不仅减少了Fxml文件的大小，也使得样式的维护更为集