步进电机传感器融合：提高精度与鲁棒性，打造可靠电机系统

# 1. 步进电机基础**

步进电机是一种将电脉冲信号转换为机械角位移的电机。其工作原理基于电磁感应，当线圈通电时，会产生磁场，与转子上的永磁体相互作用，导致转子以固定的角度步进。步进电机具有结构简单、控制精度高、响应速度快等优点，广泛应用于工业自动化、医疗器械和机器人等领域。

步进电机的基本参数包括步距角、额定电流、额定电压和保持转矩。步距角是指电机每一步的旋转角度，额定电流和电压是电机正常工作所需的电气参数，而保持转矩是指电机在没有励磁电流时能保持静止位置的最大转矩。

# 2. 传感器融合技术

### 2.1 传感器原理和类型

传感器是将物理量转换为电信号的装置，在步进电机系统中，传感器用于测量电机的位置、速度、扭矩和振动等参数。常用的传感器类型包括：

| 传感器类型 | 测量参数 | 原理 |
|---|---|---|
| 光学编码器 | 位置、速度 | 光电扫描 |
| 霍尔传感器 | 位置 | 磁场感应 |
| 电流传感器 | 电流、扭矩 | 电磁感应 |
| 加速度计 | 振动 | 压电效应 |

### 2.2 传感器数据融合算法

传感器融合算法将来自多个传感器的测量数据进行融合，以获得更准确和鲁棒的信息。常用的传感器融合算法包括：

- **卡尔曼滤波：**一种递归算法，通过预测和更新状态估计来处理测量噪声和模型不确定性。
- **扩展卡尔曼滤波：**卡尔曼滤波的非线性扩展，适用于非线性系统。
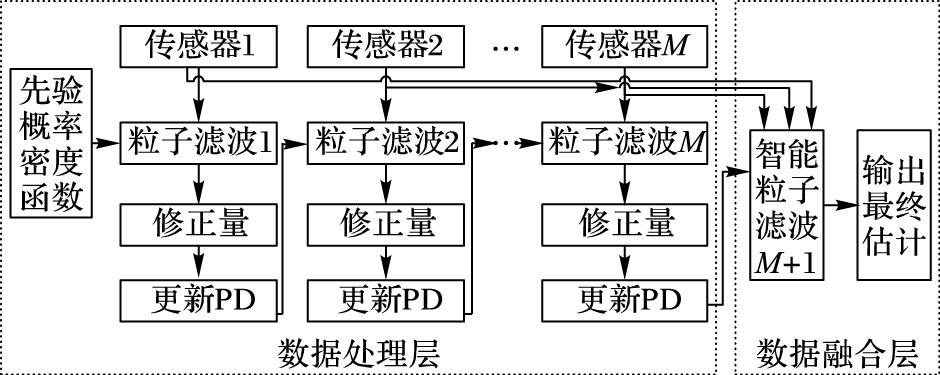
- **粒子滤波：**一种蒙特卡罗方法，通过生成和加权粒子来估计状态分布。

**代码块 1：卡尔曼滤波算法**

def kalman_filter(x, P, A, B, u, H, R, Q):
    """
    卡尔曼滤波算法

    参数：
        x: 状态估计
        P: 状态协方差矩阵
        A: 状态转移矩阵
        B: 控制输入矩阵
        u: 控制输入
        H: 观测矩阵
        R: 观测噪声协方差矩阵
        Q: 过程噪声协方差矩阵
    """

    # 预测
    x = A @ x + B @ u
    P = A @ P @ A.T + Q

    # 更新
    K = P @ H.T @ np.linalg.inv(H @ P @ H.T + R)
    x = x + K @ (y - H @ x)
    P = (np.eye(x.shape[0]) - K @ H) @ P

    return x, P

**逻辑分析：**

该代码实现了卡尔曼滤波算法，通过预测和更新步骤，估计状态和协方差矩阵。预测步骤使用状态转移矩阵和控制输入更新状态估计，更新步骤使用观测矩阵和观测值更新状态估计和协方差矩阵。

**参数说明：**

- `x`: 状态估计
- `P`: 状态协方差矩阵
- `A`: 状态转移矩阵
- `B`: 控制输入矩阵
- `u`: 控制输入
- `H`: 观测矩阵
- `R`: 观测噪声协方差矩阵
- `Q`: 过程噪声协方差矩阵

**代码块 2：扩展卡尔曼滤波算法**

def extended_kalman_filter(x, P, f, h, u, y):
    """
    扩展卡尔曼滤波算法

    参数：
        x: 状态估计
        P: 状态协方差矩阵
        f: 状态转移函数
        h: 观测函数
        u: 控制输入
        y: 观测值
    """

    # 预测
    x = f(x, u)
    F = np.array(jacobian(f, x, u))
    P = F @ P @ F.T + Q

    # 更新
    H = np.array(jacobian(h, x))
    K = P @ H.T @ np.linalg.inv(H @ P @ H.T + R)
    x = x + K @ (y - h(x))
    P = (np.eye(x.shape[0]) - K @ H) @ P

    return x, P

**逻辑分析：**

该代码实现了扩展卡尔曼滤波算法，通过使用雅可比矩阵对状态转移函数和观测函数进行线性化，来处理非线性系统。

**参数说明：**

- `x`: 状态估计
- `P`: 状态协方差矩阵
- `f`: 状态转移函数
- `h`: 观测函数
- `u`: 控制输入
- `y`: 观测值

**mermaid流程图：传感器融合算法流程**

graph LR
subgraph 传感器数据获取
    A[传感器数据获取]
end
subgraph 传感器融合算法
    B[传感器融合算法]
end
subgraph 状态估计
    C[状态估计]
e