【统计学意义的验证集】：理解验证集在机器学习模型选择与评估中的重要性

# 1. 验证集的概念与作用

在机器学习和统计学中，验证集是用来评估模型性能和选择超参数的重要工具。**验证集**是在训练集之外的一个独立数据集，通过对这个数据集的预测结果来估计模型在未见数据上的表现，从而避免了过拟合问题。验证集的作用不仅仅在于选择最佳模型，还能帮助我们理解模型在实际应用中的泛化能力，是开发高质量预测模型不可或缺的一部分。

## 1.1 验证集与训练集、测试集的区分

- **训练集**：用于训练模型的大量数据。
- **验证集**：用于调整模型参数和选择模型的集合。
- **测试集**：在模型最终评估阶段用于测试模型性能的数据。

## 1.2 验证集的作用

1. **模型选择**：比较不同模型在验证集上的表现，选择表现最好的模型。
2. **超参数调整**：通过验证集的性能反馈来调整模型的超参数。
3. **避免过拟合**：确保模型能够泛化到未见数据上，减少过拟合的风险。

通过理解验证集的定义、作用和它与其他数据集的区别，可以让我们更好地管理和优化机器学习项目。在后续章节中，我们将深入探讨统计学意义及其在验证集使用中的重要性，以及验证集在机器学习中的应用、选择策略和面临的挑战。

# 2. 理解统计学意义

统计学意义是科学研究中用来衡量结果可靠性的关键指标，它可以帮助我们确定观察到的效应是否具有普遍性，而非仅仅是偶然发生的。统计学意义的概念是数据分析和机器学习模型评估不可或缺的一部分，尤其在假设检验、模型选择和验证中扮演着至关重要的角色。

## 2.1 统计学基础概念

### 2.1.1 统计量与参数

在统计学中，统计量是从样本中计算出来的，用于估计总体参数的量。参数指的是描述总体特征的固定值，如均值、方差等，而统计量则是这些参数的估计值，其值会随着样本的不同而发生变化。

- **均值（Mean）**：衡量数据集中趋势的中心点。
- **方差（Variance）**：衡量数据分布的离散程度。
- **标准差（Standard Deviation）**：方差的平方根，也用于衡量数据的离散程度。

通过使用不同的统计量，研究者可以估计总体参数并推断总体的性质。在机器学习中，模型参数指的是用于定义模型的权重和偏差等，而统计量则包括准确率、召回率等性能指标。

### 2.1.2 假设检验的基本原理

假设检验是统计学中用于检验样本数据是否支持关于总体参数的假设的方法。它基于以下两个假设：

- **零假设（Null Hypothesis, H0）**：通常表示无效应或无差异，例如，两个组之间的平均值没有显著差异。
- **备择假设（Alternative Hypothesis, H1 或 Ha）**：与零假设相对立的假设，表示有效应或有差异。

检验过程中，我们会计算一个统计量，并将其与预先设定的显著性水平进行比较。如果统计量超过临界值，则拒绝零假设，认为有足够的证据支持备择假设；反之，则没有足够的证据拒绝零假设，结果可能是偶然的。

## 2.2 统计学意义的计算方法

### 2.2.1 P值的计算与解释

P值是在零假设为真的条件下，观察到当前结果或更极端结果的概率。它提供了评估结果偶然性的量化手段。一个较小的P值（通常小于0.05）意味着观察到的结果不太可能是偶然发生的，因此我们拒绝零假设，认为统计学上有显著性。

P值的计算依赖于选定的统计测试和数据本身。例如，在t检验中，P值会随着样本均值与总体均值差异的大小、样本的标准差以及样本数量的变化而变化。

### 2.2.2 效应量与统计功效

效应量（Effect Size）是指实验或观测中的效应的大小，是衡量结果重要性的一个统计量。它不依赖于样本大小，因此可以比较不同研究之间的结果。

统计功效（Statistical Power）是指在备择假设正确的情况下，实验正确拒绝零假设的概率。它等于1减去犯第二类错误（β错误）的概率。统计功效越高，研究结果的可信度越高。

在模型选择中，效应量可以帮助我们理解模型改善的实际意义，而统计功效则可以帮助我们了解在当前实验设计下检测到真实效应的可能性有多大。

## 2.3 统计学意义与模型选择

### 2.3.1 模型优化的目标函数

在机器学习中，目标函数是评估模型预测性能的统计量，通常用来指导模型优化。常见的目标函数包括均方误差（MSE）、交叉熵（Cross-Entropy）等。这些函数的值越小，说明模型的预测越准确。

- **均方误差**：用于回归问题，衡量模型预测值与实际值差异的平方的期望。
- **交叉熵**：常用于分类问题，衡量概率分布之间差异的度量。

目标函数的选择与优化目标紧密相关，对于不同的问题，选择合适的统计量来衡量模型性能是至关重要的。

### 2.3.2 理解过拟合与欠拟合

过拟合（Overfitting）是指模型在训练数据上表现很好，但在新数据上表现不佳的现象。其原因可能是模型过于复杂，学习了训练数据中的噪声而非真实规律。

欠拟合（Underfitting）是指模型在训练和新数据上表现都较差，通常是由于模型过于简单，无法捕捉数据的真实结构。

在机器学习模型选择时，统计学意义可以帮助我们了解模型的泛化能力，选择既不过拟合也不欠拟合的模型。通过统计量，例如验证集上的性能评估，我们可以量化模型的过拟合程度和泛化能力，从而优化模型结构和参数。

# 3. 验证集在机器学习中的应用

在机器学习领域，验证集的设置对于模型的训练和评估具有决定性作用。本章将深入探讨验证集在机器学习中的应用，重点分析其在模型选择和性能评估中的角色，并且通过案例分析，展示验证集如何影响模型的选择。

## 3.1 训练集、验证集与测试集的区别

在模型开发过程中，数据集通常被划分为三个主要部分：训练集、验证集和测试集。每部分数据都有其特定的用途和重要性。

### 3.1.1 数据集划分的原则

数据集划分的原则是保证每个部分都尽可能地反映总体样本的分布，同时避免不同部分之间的重叠。训练集用于模型的训练过程，即调整模型权重和参数的过程；验证集用于模型调优，通过验证集的性能来选择模型或调整模型的超参数；测试集则用于模型最终评估，它是在模型开发过程的最后阶段使用，目的是为了评估模型在未知数据上的表现。以下是其详细的划分原则：

- **独立性**：测试集需要独立于训练集和验证集，以确保评估结果的客观性。
- **代表性**：所有数据集应当能够代表总体数据的分布，以减少偏差。
- **比例性**：在一些情况下，三个部分的比例可能需要根据实际问题和数据集的大小进行调整。

### 3.1.2 交叉验证与留一法

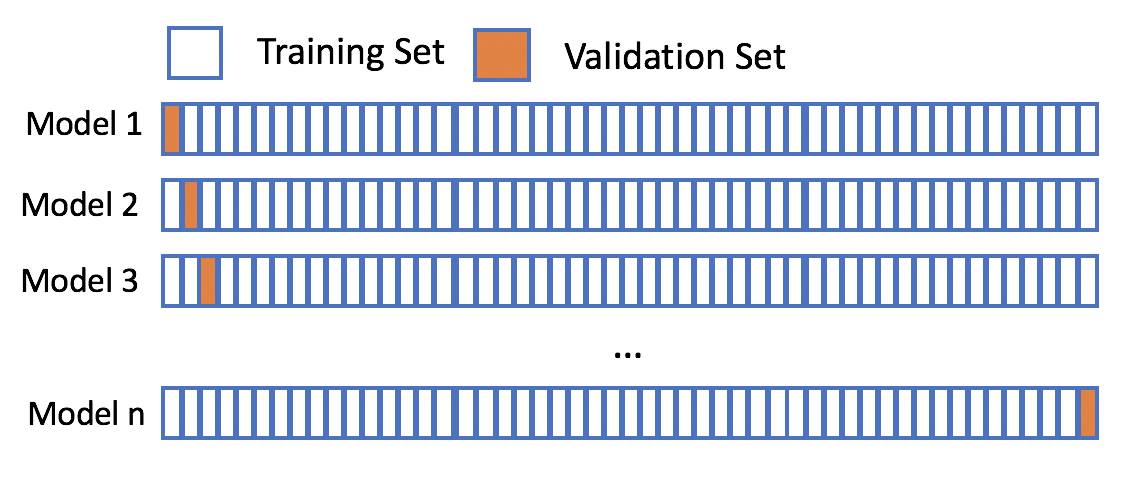
交叉验证（Cross-Validation）和留一法（Leave-One-Out）是两种常用的验证方法，它们通过不同方式划分数据集，并多次使用模型，以得到更可靠的性能评估。

- **交叉验证**：通过将数据集分成K个大小相等的子集，每次使用K-1个子集进行训练，1个子集进行验证，重复K次，每次使用不同的子集作为验证集，以减少模型估计的方差。
- **留一法**：类似于交叉验证，留一法可以看作是K折交叉验证的一个特例，其中K等于样本总数，每次仅用一个样本作为验证集，其余作为训练集。

下面的mermaid流程图展示了交叉验证的过程：

flowchart LR
    A[开始] --> B[划分K折]
    B --> C[第1轮]
    C --> D[训练集1]
    C --> E[验证集1]
    D --> |模型训练| D
    E --> |性能评估| E
    C --> F[第2轮