【时间序列分析的验证】：验证集在时间序列中的策略与案例研究

# 1. 时间序列分析基础

时间序列分析是预测未来趋势和模式的一种统计方法。它是数据分析领域中的一个重要分支，尤其在金融市场、气象预测、经济分析等需要处理时序数据的领域被广泛使用。

时间序列分析的基础首先是理解数据的基本特征。这包括数据的频率（按天、月、年等收集数据），以及数据的平稳性和非平稳性。平稳性意味着数据的统计特性不随时间改变，而非平稳性数据的统计特性会随时间变化。

时间序列可以进一步被分解为趋势、季节性和周期性成分。趋势指的是数据随时间的长期增长或下降趋势；季节性成分反映在固定时间间隔出现的规律性变动；周期性则是指非固定长度的周期性波动。

graph LR
    A[时间序列分析基础] --> B[理解数据基本特征]
    B --> C[趋势]
    B --> D[季节性]
    B --> E[周期性]

在本章中，我们将探讨时间序列分析的这些核心概念，为之后深入的时间序列理论和实践技巧章节打下坚实的基础。

# 2. 时间序列的理论框架

## 2.1 时间序列数据的特点

### 2.1.1 稳定性与非稳定性

时间序列数据的稳定性是指时间序列的统计特性，如均值和方差，在整个时间跨度内是恒定的。对于平稳时间序列，我们可以通过历史数据预测未来的点，因为未来的统计特性与过去是相似的。非稳定时间序列则是指其统计特性随时间发生变化，常见于经济、金融和气象等领域。

**表格：平稳与非平稳时间序列的对比**

| 特性 | 稳定时间序列 | 非稳定时间序列 |
|------|-------------|---------------|
| 均值 | 恒定 | 变化 |
| 方差 | 恒定 | 变化或具有趋势 |
| 相关性 | 短期相关 | 长期相关或趋势 |

在非稳定序列中，我们通常使用差分等方法使其转换为稳定序列，以适用于传统的统计方法。例如，一阶差分是指序列中每一点与前一点的差异，这种方法可以帮助去除趋势和季节性。

**代码块：使用Python进行一阶差分**

import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose

# 示例数据集
data = pd.Series([1, 2, 3, 2, 1, 2, 3, 4, 3, 2, 1])

# 检查数据的稳定性
decomposition = seasonal_decompose(data, model='additive')
decomposition.plot()
plt.show()

# 一阶差分
data_diff = data.diff().dropna()
print(data_diff)

# 再次检查差分后数据的稳定性
decomposition_diff = seasonal_decompose(data_diff, model='additive')
decomposition_diff.plot()
plt.show()

逻辑分析：在上面的代码中，首先创建一个时间序列并使用`seasonal_decompose`函数来查看其稳定性特征。然后计算一阶差分，并对差分后的序列进行类似的分解。差分后的序列通常会展示出更加稳定的特点。

### 2.1.2 趋势、季节性和周期性

时间序列数据可能包含趋势、季节性和周期性，这些成分共同定义了序列的整体行为。

- **趋势（Trend）** 指的是时间序列的长期方向或增长，可能上升、下降或稳定。
- **季节性（Seasonality）** 是指数据在固定时间间隔（如年、季度、月或周）内重复的模式。
- **周期性（Cyclicity）** 通常指比季节性更宽泛的时间周期内的波动，周期性变化不固定在特定的季节。

**mermaid流程图：时间序列成分的相互作用**

graph TD
    A[原始时间序列] --> B{趋势}
    A --> C[季节性]
    A --> D[周期性]
    B --> E[趋势去除后时间序列]
    C --> E
    D --> E
    E --> F[季节性调整]
    E --> G[周期性分析]

在实际应用中，理解并分离这些成分对于建立有效的预测模型至关重要。趋势可通过多项式拟合去除，季节性通过季节性分解方法调整，而周期性分析则需要更复杂的时间序列分解方法。

## 2.2 验证集的必要性与分类

### 2.2.1 验证集在模型评估中的作用

在时间序列分析中，验证集是用于评估模型性能的重要工具。通过使用不在模型训练期间见过的数据集对模型进行评估，可以得到对未来数据预测能力的独立验证。验证集的使用有助于调整模型参数，并减少过拟合现象的发生。

**代码块：划分训练集和验证集**

from sklearn.model_selection import TimeSeriesSplit

# 假设我们有一个时间序列数组ts
ts = np.array([...])

# 使用TimeSeriesSplit划分训练集和验证集
tscv = TimeSeriesSplit(n_splits=5)
for train_index, test_index in tscv.split(ts):
    train, test = ts[train_index], ts[test_index]
    # 在这里可以训练模型，并在验证集上评估模型

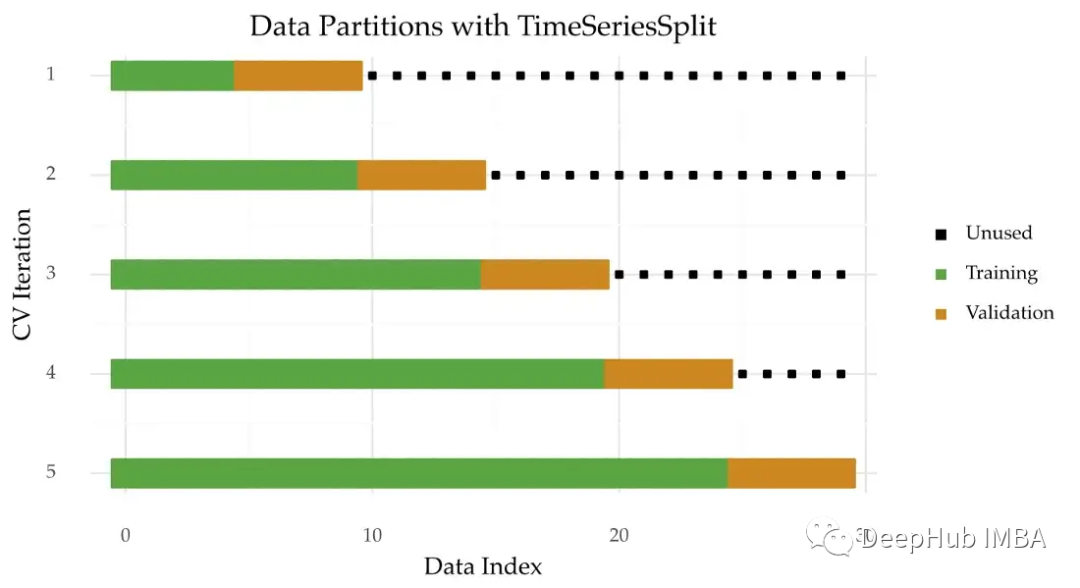
逻辑分析：在上述代码块中，我们使用了`TimeSeriesSplit`这个用于时间序列交叉验证的工具。它将数据集分割成连续的训练集和验证集。每次迭代都会使用之前的数据进行训练，而后使用后续的数据进行验证，模拟了时间序列的先后顺序。

### 2.2.2 时序数据的分割方法

时间序列数据的分割要遵循时间顺序，通常有以下几种方法：

1. **向前验证**：最直观的方法是将数据分为训练集和验证集，其中训练集在前，验证集在后。
2. **滚动预测**：在向前验证的基础上，每次验证后，将验证集的一个观测点添加到训练集中，并去掉一个最早的观测点。
3. **时间序列分割法**：比如留出最近一段作为验证集，其余作为训练集，这种方法保证了验证集与训练集之间的时间连续性。

每种方法都有其适用的场景，取决于具体问题的需求和时间序列的特性。例如，滚动预测更适用于具有短期依赖关系的时间序列数据。

## 2.3 时间序列模型的选择标准

### 2.3.1 经典时间序列模型概览

经典时间序列模型包括AR（自回归）、MA（移动平均）、ARMA（自回归移动平均）和ARIMA（自回归积分滑动平均）等。这些模型通过统计学方法来预测未来的数据点，依据历史观测值和残差来建立预测模型。

**表格：经典时间序列模型对比**

| 模型 | 特点 | 应用场景 |
|------|------|---------|
| AR | 基于当前和过去的值来预测 | 历史数据影响持续，无季节性 |
| MA | 基于过去残差的预测 | 用于短期预测 |
| ARMA | 结合AR和MA | 无季节性且短期依赖时间序列 |
| ARIMA| 结合AR、MA和差分 | 适用于非平稳时间序列 |

模型选择取决于数据的特征，例如，ARIMA模型通常在数据非平稳时使用，而ARMA适用于平稳时间序列。

### 2.3.2 模型选择的统计指标

在选择模型时，我们需要依据一些统计指标，如均方误差（MSE）、均方根误差（RMSE）、均值绝对误差（MAE）等，来衡量模型的预测性能。

**代码块：评估模型性能**

from sklearn.metrics import mean_squared_error, mean_abso