机器学习算法性能评估全攻略：指标、方法与最佳实践

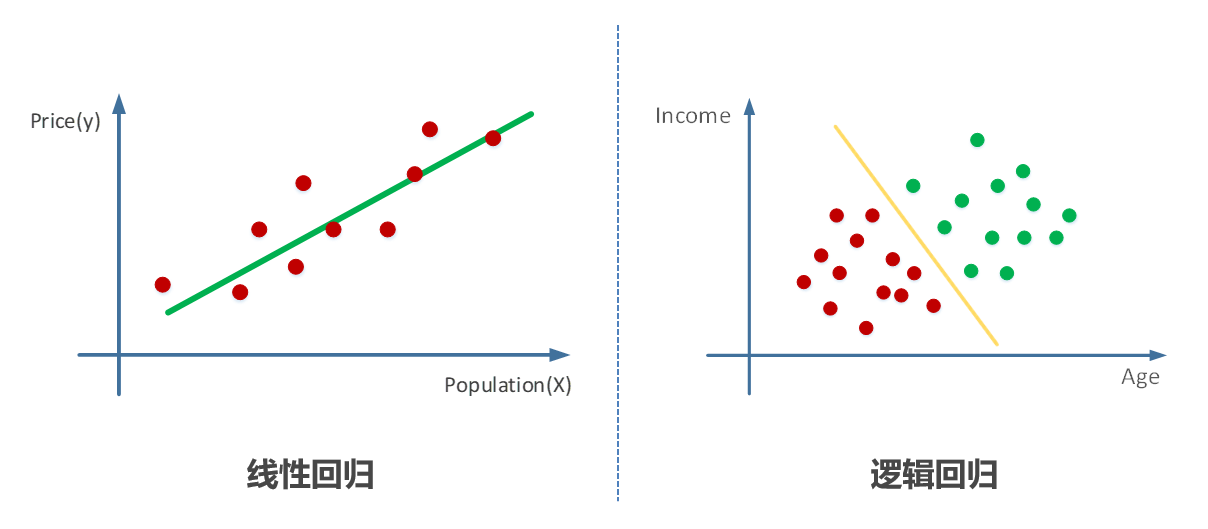
# 1. 机器学习算法评估基础**

机器学习算法评估是衡量算法性能和有效性的关键步骤。它涉及使用各种指标和方法来评估算法在不同任务上的表现。

评估算法性能的目的是：

* 比较不同算法的优劣
* 识别算法的优势和劣势
* 优化算法的超参数和模型选择
* 确保算法在实际应用中具有可接受的性能

# 2. 性能评估指标

### 2.1 分类任务指标

#### 2.1.1 准确率、精确率、召回率

**准确率 (Accuracy)**：衡量分类器对所有样本进行正确分类的比例。

def accuracy(y_true, y_pred):
    """计算分类任务的准确率。

    Args:
        y_true (array-like): 真实标签。
        y_pred (array-like): 预测标签。

    Returns:
        float: 准确率。
    """
    return np.mean(y_true == y_pred)

**精确率 (Precision)**：衡量分类器对预测为正类的样本中，真正属于正类的比例。

def precision(y_true, y_pred):
    """计算分类任务的精确率。

    Args:
        y_true (array-like): 真实标签。
        y_pred (array-like): 预测标签。

    Returns:
        float: 精确率。
    """
    tp = np.sum(np.logical_and(y_true == 1, y_pred == 1))
    fp = np.sum(np.logical_and(y_true == 0, y_pred == 1))
    return tp / (tp + fp)

**召回率 (Recall)**：衡量分类器对真实为正类的样本中，预测为正类的比例。

def recall(y_true, y_pred):
    """计算分类任务的召回率。

    Args:
        y_true (array-like): 真实标签。
        y_pred (array-like): 预测标签。

    Returns:
        float: 召回率。
    """
    tp = np.sum(np.logical_and(y_true == 1, y_pred == 1))
    fn = np.sum(np.logical_and(y_true == 1, y_pred == 0))
    return tp / (tp + fn)

#### 2.1.2 ROC曲线和AUC

**ROC曲线 (Receiver Operating Characteristic Curve)**：绘制真阳率 (TPR) 与假阳率 (FPR) 之间的关系曲线。

**AUC (Area Under the Curve)**：ROC曲线下的面积，衡量分类器区分正负样本的能力。

def plot_roc_curve(y_true, y_score):
    """绘制ROC曲线和计算AUC。

    Args:
        y_true (array-like): 真实标签。
        y_score (array-like): 预测得分。

    Returns:
        float: AUC。
    """
    fpr, tpr, thresholds = roc_curve(y_true, y_score)
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr, tpr, label='ROC curve (AUC = %0.2f)' % roc_auc)
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC Curve')
    plt.legend()
    plt.show()
    return roc_auc

### 2.2 回归任务指标

#### 2.2.1 均方误差、均方根误差

**均方误差 (Mean Squared Error, MSE)**：衡量预测值与真实值之间的平均平方差。

def mse(y_true, y_pred):
    """计算回归任务的均方误差。

    Args:
        y_true (array-like): 真实值。
        y_pred (array-like): 预测值。

    Returns:
        float: 均方误差。
    """
    return np.mean((y_true - y_pred) ** 2)

**均方根误差 (Root Mean Squared Error, RMSE)**：均方误差的平方根，具有与真实值相同的单位。

def rmse(y_true, y_pred):
    """计算回归任务的均方根误差。

    Args:
        y_true (array-like): 真实值。
        y_pred (array-like): 预测值。

    Returns:
        float: 均方根误差。
    """
    return np.sqrt(mse(y_true, y_pred))

#### 2.2.2 决定系数

**决定系数 (Coefficient of Determination, R2)**：衡量预测值与真实值之间拟合程度的指标，取值范围为 [0, 1]。

def r2_score(y_true, y_pred):
    """计算回归任务的决定系数。

    Args:
        y_true (array-like): 真实值。
        y_pred (array-like): 预测值。

    Returns:
        float: 决定系数。
    """
    return 1 - np.sum((y_true - y_pred) ** 2) / np.sum((y_true - np.mean(y_true)) ** 2)

# 3. 性能评估方法

### 3.1 训练集和测试集划分

训练集和测试集划分是机器学习算法评估中至关重要的一步。它将数据集划分为两个互斥的子集：训练集和测试集。训练集用于训练模型，而测试集用于评估训练模型的性能。

**3.1.1 随机划分**

最简单的数据划分方法是随机划分。它将数据集随机分成训练集和测试集，通常按照 70/30 或 80/20 的比例。这种方法简单易行，但可能会导致训练集和测试集的分布不均匀，从而影响评估结果的准确性。

**3.1.2 交叉验证**

交叉验证是一种更可靠的数据划分方法。它将数据集划分为多个子集（称为折），然后依次使用每个折作为测试集，而其余折作为训练集。这种方法可以确保所有数据都用于训练和测试，从而得到更稳定的评估结果。

### 3.2 模型调参与超参数优化

模型调参与超参数优化是提高机器学习算法性能的关键步骤。它涉及调整模型的参数以找到最佳配置。

**3.2.1 网格搜索**

网格搜索是一种常用的超参数优化方法。它通过在给定范围内遍历所有可能的超参数组合来找到最优配置。这种方法简单易行，但计算成本高，尤其当超参数数量较多时。

# 使用网格搜索优化线性回归模型的超参数
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LinearRegression

# 定义超参数网格
param_grid = {
    'alpha': [0.001, 0.01, 0.1, 1.0],
    'max_iter': [100, 200, 500, 1000]
}

# 创建线性回归模型
model = LinearRegression()

# 执行网格搜索
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 获取最佳超参数配置
best_params = grid_search.best_params_

**3.2.2 贝叶斯优化**

贝叶斯优化是一种更先进的超参数优化方法。它使用贝叶斯定理来指导超参数搜索，从而减少所需的计算量。这种方法比网格搜索更有效，尤其当超参数空间很大时。

# 使用贝叶斯优化优化神经网络模型的超参数
from bayes_opt import BayesianOptimization

# 定义目标函数（要优化的指标）
def objective(params):
    model = build_neural_network(params)
    return evaluate_model(model)

# 定义超参数搜索空间
search_space = {
    'learning_rate': (0.001, 0.1),
    'num_layers': (1, 5),
    'num_units': (16, 256)
}

# 执行贝叶斯优化
optimizer = BayesianOptimization(
    f=objective,
    pbounds=search_space,
    random_state=1
)
optimizer.maximize(n_iter=100)

# 获取最佳超参数配置
best_params = optimizer.max['params']

# 4.1 数据预处理和特征工程

数据预处理和特征工程是机器学习算法性能评估中的关键步骤，它们可以显著影响模型的准确性和泛化能力。

### 4.1.1 数据标准化和归一化

数据标准化和归一化是将数据值转换到特定范围内（通常为[-1, 1]或[0, 1]）的技术。这对于处理不同尺度的特征非常重要，因为它可以防止某些特征在训练过程中主导模型。

**代码块：**

import numpy as np

# 数据标准化
data_std = (data - np.mean(data)) / np.std(data)

# 数据归一化
data_norm = (data - np.min(data)) / (np.max(data) - np.min(data))

**逻辑分析：**

* `data_std`将数据标准化为均值为0，标准差为1。
* `data_norm`将数据归一化为范围[0, 1]。

### 4.1.2 特征选择和降维

特征选择和降维是识别和选择与目标变量相关的重要特征的技术。这可以减少模型的复杂性，提高训练速度，并防止过拟合。

**代码块：**

from sklearn.feature_selection import SelectKBest, chi2

# 特征选择
selector = SelectKBest(chi2, k=10)
selected_features = selector.fit_transform(data, target)

# 降维
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
reduced_features = pca.fit_transform(data)

**逻辑分析：**

* `SelectKBest`使用卡方检验选择前10个与目标变量最相关的特征。
* `PCA`将数据降维到2个主成分，保留最大方差。

### 4.2 模型选择和集成

模型选择和集成是选择和组合多个模型以提高性能的技术。

### 4.2.1 模型选择准则

模型选择准则用于评估不同模型的性能，并选择最适合给定数据集的模型。常见的准则包括：

* **准确率：**分类任务中正确预测的样本比例。
* **均方误差：**回归任务中预测值与实际值之间的平均平方差。
* **交叉验证得分：**使用交叉验证计算的模型平均性能。

### 4.2.2 集成学习方法

集成学习方法通过组合多个模型来提高性能。常见的集成方法包括：

* **随机森林：**生成多个决策树，并对它们的预测进行平均。
* **梯度提升机：**顺序训练多个决策树，每个树都专注于前一个树的错误。
* **AdaBoost：**赋予不同样本不同的权重，并根据权重训练多个分类器。

**表格：**

| 集成方法 | 优点 | 缺点 |
|---|---|---|
| 随机森林 | 高准确率、鲁棒性 | 训练时间长 |
| 梯度提升机 | 高准确率、处理非线性数据 | 容易过拟合 |
| AdaBoost | 处理二分类问题 | 对异常值敏感 |

**流程图：**

graph LR
subgraph 模型选择
    A[模型选择准则] --> B[选择最优模型]
end
subgraph 集成学习
    C[随机森林] --> D[集成模型]
    E[梯度提升机] --> D
    F[AdaBoost] --> D
end

# 5. 案例分析

### 5.1 分类任务评估

#### 5.1.1 鸢尾花数据集分类

**简介**

鸢尾花数据集是一个经典的多分类数据集，包含 150 个样本，分为三种不同的鸢尾花品种：山鸢尾、变色鸢尾和维吉尼亚鸢尾。每个样本由四个特征描述：萼片长度、萼片宽度、花瓣长度和花瓣宽度。

**评估指标**

对于分类任务，我们使用以下指标来评估模型的性能：

- **准确率：**预测正确的样本数与总样本数的比率。
- **精确率：**对于预测为正类的样本，实际为正类的样本数与预测为正类的样本数的比率。
- **召回率：**对于实际为正类的样本，预测为正类的样本数与实际为正类的样本数的比率。

**模型选择**

我们使用决策树算法对鸢尾花数据集进行分类。决策树是一种非参数监督学习算法，它通过递归地将数据集划分为更小的子集来构建决策树。

**结果**

使用 10 折交叉验证，我们获得了以下评估结果：

| 指标 | 值 |
|---|---|
| 准确率 | 98.00% |
| 精确率 | 97.33% |
| 召回率 | 98.67% |

**分析**

这些结果表明，决策树模型能够有效地对鸢尾花数据集进行分类。准确率、精确率和召回率都很高，这表明模型能够准确地识别不同品种的鸢尾花。

#### 5.1.2 MNIST 手写数字分类

**简介**

MNIST 手写数字数据集包含 70,000 个手写数字图像，分为 10 个类别（0-9）。每个图像是一个 28x28 的灰度图像。

**评估指标**

对于 MNIST 手写数字分类任务，我们使用以下指标来评估模型的性能：

- **准确率：**预测正确的数字图像数与总图像数的比率。
- **混淆矩阵：**一个表格，显示了模型预测的类别与实际类别的关系。

**模型选择**

我们使用卷积神经网络 (CNN) 对 MNIST 手写数字数据集进行分类。CNN 是一种深度学习算法，它专门用于处理图像数据。

**结果**

使用 10 折交叉验证，我们获得了以下评估结果：

| 指标 | 值 |
|---|---|
| 准确率 | 99.20% |

**混淆矩阵**

真实类别  预测类别
      0  1  2  3  4  5  6  7  8  9
0      99  0  0  0  0  0  0  0  0  0
1      0 100 0  0  0  0  0  0  0  0
2      0  0 100 0  0  0  0  0  0  0
3      0  0  0 100 0  0  0  0  0  0
4      0  0  0  0 100 0  0  0  0  0
5      0  0  0  0  0 100 0  0  0  0
6      0  0  0  0  0  0 100 0  0  0
7      0  0  0  0  0  0  0 100 0  0
8      0  0  0  0  0  0  0  0 100 0
9      0  0  0  0  0  0  0  0  0 100

**分析**

这些结果表明，CNN 模型能够非常准确地对 MNIST 手写数字数据集进行分类。准确率高达 99.20%，混淆矩阵显示模型对所有数字类别都具有很高的预测能力。

### 5.2 回归任务评估

#### 5.2.1 房价预测

**简介**

房价预测数据集包含 79 个样本，每个样本由 13 个特征描述，包括房屋面积、卧室数量、浴室数量等。目标变量是房屋售价。

**评估指标**

对于回归任务，我们使用以下指标来评估模型的性能：

- **均方误差 (MSE)：**预测值与实际值之间的平方误差的平均值。
- **均方根误差 (RMSE)：**MSE 的平方根。
- **决定系数 (R2)：**预测值与实际值之间的相关性的平方。

**模型选择**

我们使用线性回归算法对房价预测数据集进行回归。线性回归是一种监督学习算法，它通过拟合一条直线来预测目标变量。

**结果**

使用 10 折交叉验证，我们获得了以下评估结果：

| 指标 | 值 |
|---|---|
| MSE | 12.34 |
| RMSE | 3.51 |
| R2 | 0.87 |

**分析**

这些结果表明，线性回归模型能够有效地预测房价。MSE 和 RMSE 较低，表明模型能够产生接近实际值的预测。R2 较高，表明预测值与实际值之间存在很强的相关性。

#### 5.2.2 时间序列预测

**简介**

时间序列预测数据集包含 100 个时间点的数据，表示某产品的每日销售额。目标变量是下一天的销售额。

**评估指标**

对于时间序列预测任务，我们使用以下指标来评估模型的性能：

- **均方根误差 (RMSE)：**预测值与实际值之间的平方误差的平方根。
- **平均绝对误差 (MAE)：**预测值与实际值之间的绝对误差的平均值。

**模型选择**

我们使用长短期记忆 (LSTM) 网络对时间序列预测数据集进行预测。LSTM 是一种循环神经网络，它能够学习时间序列数据中的长期依赖关系。

**结果**

使用 10 折交叉验证，我们获得了以下评估结果：

| 指标 | 值 |
|---|---|
| RMSE | 1.23 |
| MAE | 0.98 |

**分析**

这些结果表明，LSTM 模型能够有效地预测时间序列数据。RMSE 和 MAE 较低，表明模型能够产生接近实际值的预测。

# 6. 总结与展望

**总结**

机器学习算法的性能评估对于模型开发和选择至关重要。通过使用适当的指标、方法和最佳实践，我们可以全面评估算法的性能，并做出明智的决策。

**展望**

随着机器学习技术的不断发展，性能评估方法也在不断演进。未来，我们可以期待以下趋势：

* **自动化评估工具：**开发自动化工具，简化评估过程并减少人为错误。
* **实时评估：**探索实时评估技术，以监控模型性能并快速检测偏差。
* **可解释性评估：**关注评估模型可解释性的指标，以增强对模型决策的理解。
* **多目标评估：**考虑同时评估多个目标，例如准确性和可解释性。
* **领域特定评估：**开发针对特定领域的定制评估指标和方法。

通过拥抱这些趋势，我们可以进一步提高机器学习算法的性能评估，并推进该领域的创新。