机器人移动平台设计思路：案例分析与设计方法全解析


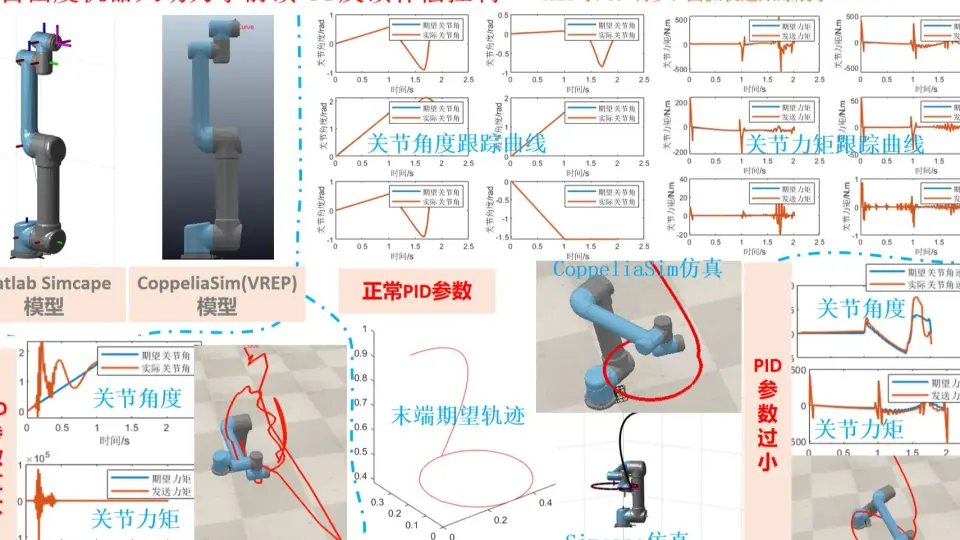
# 摘要
本文从机器人移动平台的设计出发，全面概述了移动平台的基本理论，包括运动学基础、控制理论与算法、环境感知与数据融合技术。通过对硬件结构、软件架构设计以及系统集成与调试的深入分析，探讨了机器人移动平台设计实践的多个关键方面。结合特定应用场景的案例分析，本文揭示了机器人移动平台在设计与实施过程中遇到的问题以及相应的解决方案和创新点。最后，文章展望了移动平台技术的未来发展趋势，包括新兴技术的影响、设计理念与方法的创新，以及跨学科融合与应用扩展的可能性。

# 关键字
机器人移动平台；运动学；控制算法；数据融合；系统集成；案例分析

参考资源链接：[机器人学导论课后习题答案](https://wenku.csdn.net/doc/30d6086euy?spm=1055.2635.3001.10343)
# 1. 机器人移动平台的设计概述

移动平台是机器人技术中的重要组成部分，它确保了机器人的移动性和灵活性。本章节将介绍移动平台设计的初步概念，阐述其重要性，以及如何整合不同技术以创建高效的机器人移动解决方案。

## 1.1 移动平台的作用与意义

机器人移动平台是实现机器人在物理空间自主导航和移动的关键。它包括机械结构、驱动系统、感知系统和控制系统等核心组件。这些组件协同工作，赋予机器人完成特定任务的能力。

## 1.2 设计原则与考量因素

在设计机器人移动平台时，需要考虑多方面因素，包括机器人要完成的任务类型、环境条件、成本预算以及维护便捷性等。设计原则强调平台的模块化、可靠性、可扩展性和用户友好性。

## 1.3 技术融合的重要性

现代移动平台设计不仅仅依赖于单一技术，而是多个技术领域的融合。例如，结合先进控制算法、环境感知技术与创新的能源管理系统，能够显著提升机器人的效率和适应性。

综上所述，本章节为读者提供了机器人移动平台设计的宏观视角，为后续章节中更深入的技术细节和案例分析打下基础。

# 2. 移动平台的基本理论

## 2.1 机器人运动学基础

### 2.1.1 运动学模型的建立

机器人运动学研究的是机器人各个关节以及连杆之间的相对运动关系，而不考虑力和力矩的影响。建立运动学模型是机器人设计的核心之一，它能够帮助工程师理解机器人在执行任务时各个部分的运动规律。

在二维空间中，一个机器人臂的运动学模型通常简化为一系列旋转关节和连杆。每个关节代表一个自由度（DoF），而每个连杆代表关节之间的距离。通过这样的简化，可以使用一系列的变换矩阵来表达机器人末端执行器的位置和姿态。

构建运动学模型的数学工具包括几何变换、旋转矩阵、齐次变换等。例如，一个简单的两关节机器人臂可以通过以下齐次变换矩阵来表示末端执行器的位置和姿态：

T = A_1 A_2 = 
\begin{bmatrix}
cos(\theta_1) & -sin(\theta_1) & l_1 cos(\theta_1) \\
sin(\theta_1) & cos(\theta_1) & l_1 sin(\theta_1) \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
cos(\theta_2) & -sin(\theta_2) & (l_1+l_2) cos(\theta_2) \\
sin(\theta_2) & cos(\theta_2) & (l_1+l_2) sin(\theta_2) \\
0 & 0 & 1
\end{bmatrix}

在该模型中，`\(A_1\)` 和 `\(A_2\)` 分别代表每个关节的变换矩阵，`\(l_1\)` 和 `\(l_2\)` 是连杆长度，`\(\theta_1\)` 和 `\(\theta_2\)` 是关节角。

### 2.1.2 位姿、速度和加速度的关系

为了控制机器人精确地移动到指定位置，我们需要了解位姿、速度和加速度之间的数学关系。位姿指的是机器人在三维空间中的位置和方向。速度是位姿随时间变化的导数，加速度则是速度随时间变化的导数。这些关系的数学模型为机器人控制系统提供了理论基础。

假设在三维空间中，机器人末端执行器的位姿可以表示为位置向量 `\(p\) = [x, y, z]` 和方向向量 `\(q\) = [qw, qx, qy, qz]`（使用四元数表示）。速度 `\(v\)` 和角速度 `\(\omega\)` 可以通过以下方式求导得到：

\dot{p} = v = \frac{dp}{dt}, \quad \dot{q} = \omega \times q = \frac{dq}{dt}

加速度 `\(a\)` 可以通过对速度的求导获得：

\dot{v} = a = \frac{dv}{dt}

根据上述关系，我们可以建立机器人控制系统中的运动学方程，为控制算法提供必要的数学模型。

## 2.2 控制理论与算法

### 2.2.1 控制系统的类型和要求

在机器人移动平台中，控制系统是其"大脑"。根据控制目标的不同，控制系统可以分为位置控制、速度控制和力矩控制等类型。一个好的控制系统应该能够准确、稳定地控制机器人的运动，同时具备良好的动态响应和抗干扰能力。

一个典型的控制系统通常由传感器、控制器和执行机构组成。传感器负责采集系统的当前状态信息；控制器则根据控制算法计算出误差，并生成控制信号；执行机构负责根据控制信号进行动作。

### 2.2.2 常见的控制算法分析

控制算法是实现精确控制的关键。常见的控制算法有PID（比例-积分-微分）控制、模糊控制、自适应控制、模型预测控制等。

PID控制器是工业界最常用的控制算法之一。它通过计算系统当前的误差、误差的累积（积分）和误差的变化率（微分）来调节输出，以达到控制目标。PID控制器的数学表达式如下：

u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt}

其中，`\(u(t)\)` 是控制器的输出，`\(e(t)\)` 是误差信号，`\(K_p\)`, `\(K_i\)`, `\(K_d\)` 分别是比例、积分和微分增益。

### 2.2.3 算法在移动平台中的应用案例

以PID控制器在移动机器人中的应用为例，它可以用于调整机器人的速度和方向。例如，在一个自动导航的移动平台上，PID控制算法可以用来维持机器人的速度和方向稳定，以跟踪预定的路径。

在实现过程中，首先需要设置PID控制器的三个参数：`\(K_p\)`, `\(K_i\)`, `\(K_d\)`。这通常通过试验和调整来完成，直到系统能够以最小的超调和稳定时间达到期望的性能。

# 一个简单的PID控制类实现示例
class PIDController:
    def __init__(self, kp, ki, kd):
        self.kp = kp
        self.ki = ki
        self.kd = kd
        self.previous_error = 0.0
        self.integral = 0.0
    def update(self, setpoint, measured_value, dt):
        error = setpoint - measured_value
        self.integral += error * dt
        derivative = (error - self.previous_error) / dt
        output = self.kp * error + self.ki * self.integral + self.kd * derivative
        self.previous_error = error
        return output

## 2.3 环境感知与数据融合

### 2.3.1 各类传感器的原理与选择

在机器人移动平台中，环境感知主要依靠各类传感器。常见的传感器包括激光雷达、超声波传感器、红外传感器、摄像头等。每种传感器都有其特定的工作原理和适用范围。

例如，激光雷达（LIDAR）通过发射激光并测量反射回来的光波的时间差，可以精确地测量周围环境的三维信息。而超声波传感器通过发射超声波并接收反射波，可以测量较近范围内障碍物的距离。

选择传感器时需要考虑以下因素：感知距离、精度、响应时间、体积、成本、功耗等。通常在实际应用中，会根据具体需求选择合适的传感器组合来获得最佳的环境感知效果。

### 2.3.2 数据融合技术的基本原理

数据融合技术是指将来自多个传感器的数据进行综合处理，以获得比单一传感器更准确、更可靠的信息。数据融合可以分为多个层次，包括原始数据级、特征级和决策级。

原始数据级融合是在数据采集阶段就将多个传感器的数据结合起来。特征级融合则是在特征提取之后，将不同传感器的特征进行融合。决策级融合是在每个传感器已经做出单独决策后，再进行决策的综合。

数据融合的算法有加权平均法、卡尔曼滤波、粒子滤波等。例如，卡尔曼滤波通过建立系统的动态模型，根据观测数据递归地估计系统状态。

\begin{aligned}
\hat{x}_{k|k-1} &= \hat{x}_{k-1} + \Delta t \cdot \hat{f}(\hat{x}_{k-1}, u_k) \\
P_{k|k-1} &= F_k P_{k-1} F_k^T + Q_k \\
y_k &= z_k - H_k \hat{x}_{k|k-1} \\
S_k &= H_k P_{k|k-1} H_k^T + R_k \\
K_k &= P_{k|k-1} H_k^T S_k^{-1} \\
\hat{x}_{k} &= \hat{x}_{k|k-1} + K_k y_k \\
P_k &= (I - K_k H_k) P_{k|k-1}
\end{aligned}

其中，`\(x\)` 是状态向量，`\(z\)` 是观测向量，`\(u\)` 是控制输入，`\(P\)` 是估计误差的协方差，`\(Q\)` 和 `\(R\)` 分别是系统噪声和观测噪声的协方差，`\(F\)` 是状态转移矩阵，`\(H\)` 是观测矩阵，`\(K\)` 是卡尔曼增益，`\(S\)` 是观测的协方差，`\(I\)` 是单位矩阵。

### 2.3.3 环境感知技术的应用实例

以一个室外自动驾驶汽车为例，它使用激光雷达、摄像头和GPS等多种传