【递归算法与动态规划】：DFS在数据结构中的对比分析与实践技巧

# 1. 递归算法与动态规划基础

递归算法与动态规划是解决复杂问题时常用的两种策略。理解它们的基础概念、原理和实现方法对于一名IT专业人士来说是必不可少的。

## 1.1 递归算法的本质

递归算法是一种解决问题的方法，它将一个复杂问题分解为相似的子问题，直到达到一个简单可以解决的级别。递归算法通过函数自身调用自身的方式来逐步解决子问题，直到达到基本情况（base case）。

def factorial(n):
    # 基本情况：0! = 1
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)  # 递归调用

在上面的代码中，我们可以看到如何用递归计算阶乘。递归通过自身调用逐步将问题规模减小，直至达到基本情况。

## 1.2 动态规划的基本原理

动态规划（Dynamic Programming，DP）是一种将复杂问题分解为较小的子问题，并保存这些子问题的解以避免重复计算的方法。动态规划通常用于具有重叠子问题和最优子结构的问题。

def fibonacci(n):
    if n <= 1:
        return n
    # 利用数组存储已经计算过的值
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]

在这个例子中，我们使用了一个数组来保存斐波那契序列的每个值，以避免重复计算，这是动态规划中自底向上的典型实现。通过这种方法，我们能够有效地计算斐波那契数列的第n项。

通过上述两个简单的例子，我们可以看到递归算法和动态规划都是解决特定问题的工具，二者在原理和实现上有显著的不同。递归算法简单直观，但可能效率低下；动态规划能够有效解决递归算法中可能出现的重叠子问题，提高算法效率。掌握这两种方法对于任何寻求高效解决问题的IT从业者来说都是至关重要的。

# 2. 深度优先搜索（DFS）的理论基础

### 2.1 深度优先搜索的概念
#### 2.1.1 搜索树与递归的联系
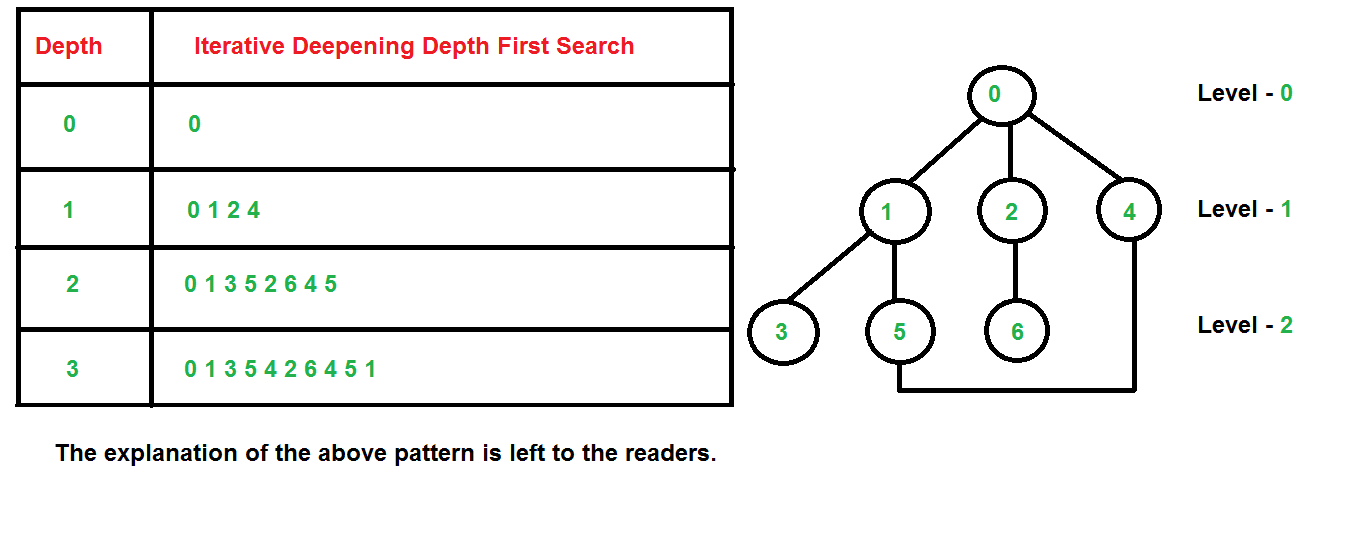
深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。该算法的执行过程模拟了现实世界中的"深度优先"逻辑，即从起始点开始，尽可能地深入到分支的末端，当到达一个节点，若该节点无未被访问的相邻节点或已经访问过，则回溯到上一个节点。

搜索树是DFS的核心概念之一，它是以树形结构展现搜索过程中节点的访问次序。每个节点都代表了算法在搜索过程中的一种状态。在树中，节点的子节点通常表示算法在当前节点进行的可能探索方向。

递归是实现DFS的重要手段，因为DFS在本质上就是一种递归的过程。它从初始节点开始，对节点的每个未被访问的子节点递归调用DFS函数，直到所有节点都被访问或者找到目标节点。

为了更加清晰地理解搜索树与递归之间的联系，以下是一个伪代码实现：

function DFS(currentNode) {
    if (currentNode is the goal) {
        processGoal(currentNode);
        return;
    }
    mark currentNode as visited;
    for each child in children of currentNode {
        if (child is not visited) {
            DFS(child);
        }
    }
    unmark currentNode as visited;
}

在这个伪代码中，我们可以看到递归的典型结构：函数调用自身来处理当前节点的子节点。递归的结束条件是找到目标节点或者没有未访问的子节点。

#### 2.1.2 DFS的典型应用场景
深度优先搜索因其简单和易于实现的特性，被广泛应用于多个领域和场景中：

- **路径寻找问题**：在图中寻找从一个节点到另一个节点的路径，尤其是在迷宫求解、地图导航等问题中。
- **拓扑排序**：在有向无环图（DAG）中确定节点的线性顺序，即拓扑排序，可用于解决课程安排、依赖管理等问题。
- **回溯算法**：在求解问题过程中，当尝试了所有可能的选项都不能得到正确答案时，回溯算法会回退并尝试新的选项。DFS常用于这类问题中，例如八皇后问题、图的着色问题等。
- **解环问题**：在有向图中检测是否存在环，以及在无向图中找出所有的环。

### 2.2 深度优先搜索的算法实现
#### 2.2.1 递归函数的基本结构
深度优先搜索的实现通常基于递归函数，递归函数的基本结构包括起始条件、递归条件、执行体和恢复现场四个部分。下面用Python代码来展示DFS的一个基本实现：

def dfs(graph, node, visited=None):
    if visited is None:
        visited = set()
    visited.add(node)  # Mark the node as visited
    process(node)  # Process the node value or print it
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)  # Recursive call for all neighbors
    visited.remove(node)  # Backtrack: Unmark the node as visited

在此代码中，`process(node)` 代表对当前节点进行操作，比如打印节点的值或者收集相关信息。函数首先标记当前节点为已访问，然后遍历所有未访问的邻居节点，并对每个邻居递归调用DFS函数。每次递归返回后，将当前节点标记为未访问，以便下一个递归调用可以重新访问该节点。

#### 2.2.2 访问标记与避免重复访问
为了避免在图或树结构中重复访问节点，通常需要使用标记结构（如数组、集合或字典）来记录节点的访问状态。以下是使用集合来记录访问过的节点的伪代码：

function DFS(currentNode, visited) {
    if (currentNode is visited or currentNode is not valid)
        return;
    mark currentNode as visited;
    process currentNode;
    for each child in children of currentNode {
        if (child is not in visited) {
            DFS(child, visited);
        }
    }
}

在DFS的实现中，访问标记是关键的一步，它确保每个节点只被访问一次，从而避免了无限循环的发生，并且提高了算法的效率。

### 2.3 深度优先搜索的优化策略
#### 2.3.1 剪枝技术
在某些复杂的搜索问题中，深度优先搜索可能会尝试大量的无效路径，这将导致算法效率低下。为了解决这个问题，可以采用剪枝技术，即在搜索过程中，根据问题的特定知识提前排除某些不可能到达目标的路径。这种方法可以大幅减少搜索空间，提升算法效率。剪枝技术的应用通常需要对问题有深入的理解。

以下是一个简单的剪枝技术应用示例，假定我们要在图中寻找一条路径，并且已知目标节点的距离大于某个阈值：

def pruned_dfs(graph, node, visited, threshold, target_distance):
    if visited[node]:
        return False
    if get_distance(node) > target_distance:
        return False
    # 其余的DFS逻辑...

在这个例子中，我们增加了一个检查，如果当前节点的已知距离超过了预设的阈值，则立即停止对此路径的进一步搜索。

#### 2.3.2 时间和空间复杂度分析
深度优先搜索的时间复杂度是O(V+E)，其中V是节点的数量，E是边的数量。这是因为DFS将访问每个节点一次，并且将探索每条边一次。空间复杂度主要取决于递归调用栈的深度，最坏情况下，如果图是完全连通的，空间复杂度是O(V)。这在图中节点很多的情况下可能会成为瓶颈。

为了优化空间复杂度，可以使用迭代的DFS实现，并通过显式栈来代替递归栈。显式栈的实现可以避免深度递归带来的栈溢出风险，并且允许更细粒度的控制。

### 2.4 深度优先搜索的复杂应用实例
深度优先搜索不仅适用于简单的图遍历，它还可以扩展到解决更复杂的问题，例如在复杂数据结构中的应用，以及结合其他算法的混合策略中。

#### 应用实例：图的遍历与网络流问题
深度优先搜索可以用于解决网络流问题。例如，在最大流算法中，DFS可以帮助找到从源点到汇点的路径，并且尽可能多地发送流量。DFS的递归结构非常适合在有向图中寻找增广路径。

#### 应用实例：组合问题的递归模型
在组合优化问题中，如旅行推销员问题（TSP），我们尝试找到一条最短的路径，使得每个城市恰好被访问一次并且返回起点。DFS可以用来枚举所有可能的路径，并且找到最短的那一条。

深度优先搜索因其强大的适应性和灵活性，在解决各类问题时都有着广泛的应用。在下一章节中，我们将深入探讨动态规划的理论基础，这是解决另一类重要问题的强大工具。

# 3. 动态规划的理论基础

动态规划是一种在数学、管理科学、计算机科学和经济学等领域中使用非常广泛的优化方法。它的核心思想是把原问题分解为相对简单的子问题，并且存储每个子问题的解，以避免重复计算。本章将深入探讨动态规划的定义、原理、算法框架以及常见类型，并以实际案例加深理解。

## 3.1 动态规划的定义与原理

动态规划是解决多阶段决策过程优化问题的一种数学方法，通过把原问题分解为相对简单的子问题的方式，自底向上（Bottom-Up）或自顶向下（Top-Down）来寻找最优解。

### 3.1.1 动态规划与分治策略

动态规划和分治策略有着明显的区别，虽然它们都采用递归的方法将问题分解，但动态规划在求解过程中更注重子问题间的重叠和计算的高效性。

- 分治策略将问题分解为若干个规模较小但类似于原问题的子问题，递归解决每个子问题，最后将子问题的解合并为原问题的解。
- 动态规划则是将原问题分解成一系列子问题后，通过动态地保存这些子问题的解（通常是