【递归终止条件设定】：数据结构DFS中的关键点与状态保存恢复

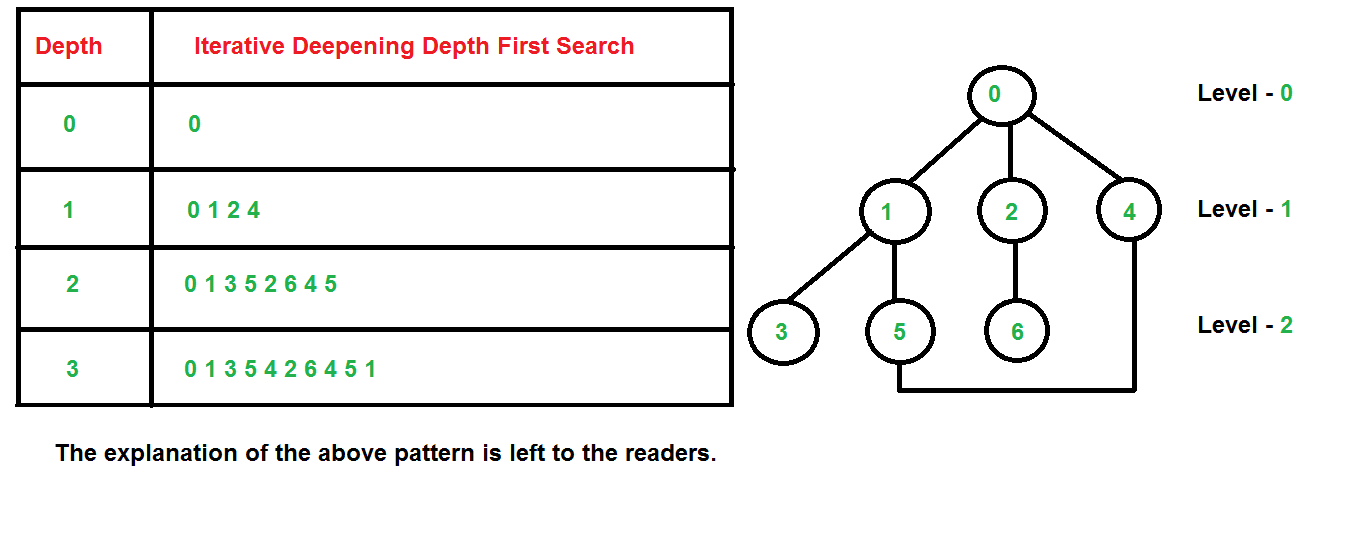
# 1. 深度优先搜索（DFS）概述

深度优先搜索（DFS）是图论中的一个基本算法，广泛应用于计算机科学领域中的各种搜索问题。在这一章节中，我们将对DFS算法进行简单介绍，并概述其在不同场景下的应用价值和基础工作原理。

首先，DFS是一种用于遍历或搜索树或图的算法。其核心思想是从一个节点开始，尽可能深地搜索图的分支。当节点v的所有出边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

在实际应用中，DFS能够帮助解决诸如路径查找、网络爬虫、迷宫求解等问题。该算法因其简洁性和实现的便捷性，在算法竞赛和实际开发中经常作为首选。

本章余下部分将深入探讨DFS的原理和应用，为理解后续章节打下基础。接下来的章节将详细解析递归终止条件的重要性，以及如何在DFS中有效保存和恢复状态，帮助读者全面掌握深度优先搜索算法。

# 2. 递归终止条件的重要性

在递归算法的设计中，正确的终止条件是至关重要的。它不仅防止了递归调用无限制地进行下去，从而避免了程序崩溃和内存溢出的风险，同时还能确保算法能够达到预期的结果。

## 2.1 递归算法的基本原理

### 2.1.1 递归的定义和工作方式

递归算法是一种在解决问题时将问题分解为更小的子问题的策略。这些子问题以相同的方式继续分解，直到它们简化为可以直接解决的最基本形式。递归的定义本质上依赖于两个要素：基本情况和递归情况。

def factorial(n):
    # 基本情况
    if n == 1:
        return 1
    # 递归情况
    else:
        return n * factorial(n - 1)

在上述阶乘函数的递归实现中，基本情况是 `n == 1`，此时返回1；递归情况则是 `n > 1`，此时函数调用自身来解决 `n-1` 的阶乘问题，并将结果乘以 `n`。

### 2.1.2 递归算法的执行堆栈理解

递归的每一次调用都会在执行堆栈上创建一个新的帧。这个帧包含了函数当前执行的状态、局部变量和返回地址。当一个递归函数结束时，控制权会返回到调用它的上一个状态，就像你在书中放了一个书签，读完一页后返回到书签位置继续阅读。

flowchart LR
    A["1! = 1"] --> B["2! = 2 * 1!"]
    B --> C["3! = 3 * 2!"]
    C --> D["4! = 4 * 3!"]
    D --> E["5! = 5 * 4!"]
    E --> F["计算结果：120"]

## 2.2 终止条件在递归中的作用

### 2.2.1 避免无限递归的必要条件

为了防止无限递归，需要明确地设定一个或多个终止条件。这些条件确保了递归在达到某个特定条件时停止。如果没有终止条件，那么递归调用将会无限进行下去，直到系统资源耗尽。

def recursive_sum(lst):
    # 基本情况：列表为空时，返回0
    if not lst:
        return 0
    # 递归情况：返回当前第一个元素加上其余元素的和
    else:
        return lst[0] + recursive_sum(lst[1:])

在该示例中，终止条件是 `lst` 为空列表，如果缺失了这样的条件，函数将无限递归调用自身，最终导致 `RecursionError`。

### 2.2.2 设定终止条件的基本规则

终止条件应满足以下基本规则：

- 明确性：它应该很容易地识别何时应该停止递归。
- 完整性：必须覆盖所有可能的执行路径，以确保不会有未处理的情况。
- 最小化：应该尽量少的设置终止条件，以减少复杂性和潜在的错误。

def find_max_element(lst, index=0):
    # 终止条件：当索引超出列表范围时停止递归
    if index >= len(lst):
        return None
    # 递归情况：返回当前最大值或递归调用找到下一个最大值
    return max(lst[index], find_max_element(lst, index + 1))

在这个例子中，终止条件被设置为索引超出列表范围，确保了递归最终能够结束。同时，我们保证了递归过程能够覆盖列表中的所有元素，遵循了完整性原则。

# 3. 深度优先搜索中的状态保存与恢复

## 3.1 状态保存的意义和方法

在深度优先搜索（DFS）的执行过程中，算法会遍历节点并尝试不同的路径来寻找解。在这个过程中，经常需要在不同的搜索点之间来回跳转，这时就需要保存和恢复算法的状态。因此，状态保存和恢复对于确保搜索能够正确返回并且能够有效地处理重复状态至关重要。

### 3.1.1 状态保存的时机选择

在DFS中，何时保存状态是决定搜索效率的关键。一般情况下，在进入子节点之前保存当前节点的状态是最佳时机。这样做的原因是在递归返回时，我们可以准确地恢复到调用前的状态，继续尝试其他路径。

为了说明这一点，我们可以考虑一个简单的例子：在遍历树形结构时，进入一个新的子节点前保存当前节点的状态，然后进入子节点，子节点遍历完成后，从保存的状态中恢复，以探索其他的分支。

### 3.1.2 状态保存的数据结构设计

选择合适的数据结构来保存状态是非常重要