MATLAB非线性方程组求解：剖析5大求解器，揭秘原理与算法

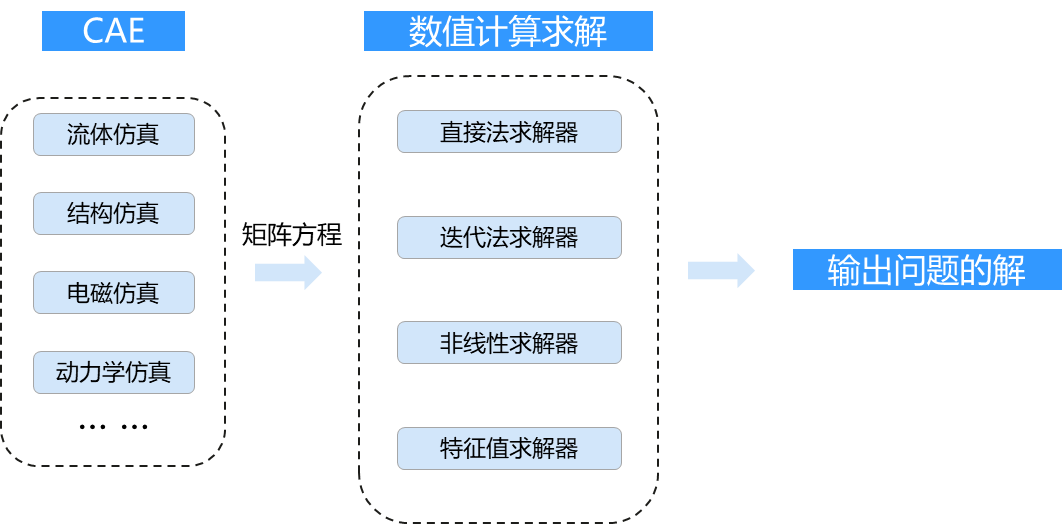
# 1. 非线性方程组求解概述**

非线性方程组是指一组包含非线性函数的方程。与线性方程组不同，非线性方程组的求解通常更具挑战性，因为它们没有通用的解析解。因此，需要使用数值方法来近似求解。

MATLAB提供了多种非线性方程组求解器，每种求解器都基于不同的算法。这些算法利用迭代方法逐步逼近解，直到满足指定的收敛准则。求解器选择取决于方程组的性质、所需的精度和可用的计算资源。

# 2. MATLAB非线性方程组求解器

### 2.1 求解器类型和原理

MATLAB提供了多种非线性方程组求解器，每种求解器都基于不同的数学原理和算法。

#### 2.1.1 牛顿法

牛顿法是一种迭代求解法，它利用函数的导数信息来逼近方程组的根。其基本原理是：

x_{n+1} = x_n - f(x_n)/f'(x_n)

其中：

- `x_n`是第`n`次迭代的近似解
- `f(x_n)`是方程组在`x_n`处的函数值
- `f'(x_n)`是方程组在`x_n`处的雅可比矩阵

牛顿法收敛速度快，但需要计算雅可比矩阵，这在方程组维度较高时计算量较大。

#### 2.1.2 拟牛顿法

拟牛顿法是一种改进的牛顿法，它不需要计算雅可比矩阵，而是利用近似值来替代。常见的拟牛顿法有：

- BFGS法
- DFP法
- SR1法

拟牛顿法收敛速度比牛顿法稍慢，但计算量更小。

#### 2.1.3 共轭梯度法

共轭梯度法是一种迭代求解法，它利用共轭梯度方向来逼近方程组的根。其基本原理是：

x_{n+1} = x_n + α_n * d_n

其中：

- `x_n`是第`n`次迭代的近似解
- `α_n`是步长
- `d_n`是共轭梯度方向

共轭梯度法收敛速度较慢，但不需要计算雅可比矩阵或其近似值。

#### 2.1.4 遗传算法

遗传算法是一种启发式求解算法，它模拟生物的进化过程来求解优化问题。其基本原理是：

1. 随机生成一组候选解（染色体）
2. 计算每个候选解的适应度
3. 选择适应度高的候选解进行交叉和变异操作
4. 重复步骤2和3，直到达到终止条件

遗传算法适用于求解复杂非线性方程组，但收敛速度慢，且容易陷入局部最优。

#### 2.1.5 粒子群优化算法

粒子群优化算法是一种启发式求解算法，它模拟鸟群或鱼群的集体行为来求解优化问题。其基本原理是：

1. 随机生成一组粒子（候选解）
2. 计算每个粒子的适应度
3. 更新每个粒子的速度和位置，使其向适应度更高的粒子靠近
4. 重复步骤2和3，直到达到终止条件

粒子群优化算法适用于求解复杂非线性方程组，但收敛速度慢，且容易陷入局部最优。

### 2.2 求解器选择和比较

#### 2.2.1 求解器性能指标

选择求解器时，需要考虑以下性能指标：

- 收敛速度：求解器找到方程组根的迭代次数
- 精度：求解器找到方程组根的近似程度
- 稳定性：求解器在不同初始值下收敛到相同根的能力
- 鲁棒性：求解器处理方程组病态或奇异情况的能力

#### 2.2.2 不同求解器适用场景

不同的求解器适用于不同的方程组类型和求解场景：

| 求解器 | 适用场景 |
|---|---|
| 牛顿法 | 方程组维度较低，函数可导 |
| 拟牛顿法 | 方程组维度较高，函数可导，计算量要求不高 |
| 共轭梯度法 | 方程组维度较高，函数不可导 |
| 遗传算法 | 方程组复杂，求解难度大 |
| 粒子群优化算法 | 方程组复杂，求解难度大 |

在实际应用中，需要根据方程组的具体特点和求解要求，选择合适的求解器。

# 3. MATLAB非线性方程组求解实践

### 3.1 求解器调用和参数设置

**3.1.1 fsolve函数**

MATLAB中求解非线性方程组的主要函数是`fsolve`。其语法如下：

x = fsolve(fun, x0, options)

其中：

* `fun`：求解的非线性方程组函数，其输入为待求解变量向量，输出为方程组残差向量。
* `x0`：初始猜测解向量。
* `options`：求解器选项，用于设置求解参数。

**3.1.2 optimset函数**

`optimset`函数用于设置求解器选项。其语法如下：

options = optimset('param1', value1, 'param2', value2, ...)

其中：

* `param1`, `param2`, ...：求解器选项名称。
* `value1`, `value2`, ...：求解器选项值。

常用的求解器选项包括：

| 选项名称 | 描述 |
|---|---|
| `Display` | 求解过程显示级别 |
| `TolFun` | 方程组残差容差 |
| `TolX` | 变量变化容差 |
| `MaxFunEvals` | 最大函数评估次数 |
| `MaxIter` | 最大迭代次数 |

### 3.2 求解过程和结果分析

**3.2.1 求解过程可视化**

MATLAB提供了`fplot`函数，可以绘制函数图像。通过绘制方程组残差函数，可以直观地观察求解过程。

% 定义方程组函数
fun = @(x) [x(1)^2 - x(2) + 1; x(1) + x(2)^2 - 4];

% 设置求解器选项
options = optimset('Display', 'iter');

% 求解方程组
x0 = [1; 1]; % 初始猜测解
[x, fval, exitflag, output] = fsolve(fun, x0, options);

% 绘制残差函数图像
fplot(fun, [0, 2], [0, 2]);
hold on;
plot(x(1), x(2), 'ro'); % 标记求解结果
xlabel('x1');
ylabel('x2');
title('残差函数图像');

**3.2.2 求解结果验证**

求解完成后，可以通过以下步骤验证求解结果：

* **检查残差向量：**求解结果的残差向量应该非常接近零。
* **代入方程组：**将求解结果代入方程组，检查是否满足方程组。
* **计算条件数：**条件数是衡量方程组求解难度的指标。条件数较大的方程组求解难度较大。

% 计算残差向量
residual = fun(x);

% 代入方程组
eq1 = x(1)^2 - x(2) + 1;
eq2 = x(1) + x(2)^2 - 4;

% 计算条件数
J = jacobian(fun, x); % 计算雅可比矩阵
condition_number = cond(J);

% 输出验证信息
disp('残差向量：');
disp(residual);
disp('方程组满足情况：');
disp(['eq1 = ', num2str(eq1)]);
disp(['eq2 = ', num2str(eq2)]);
disp(['条件数：', num2str(condition_number)]);

# 4. MATLAB非线性方程组求解高级技巧

### 4.1 问题预处理和后处理

#### 4.1.1 方程组缩放

方程组缩放是将方程组中的变量进行缩放，使得变量的量级接近，避免因变量量级差异过大导致求解器收敛困难或精度下降。缩放方法有两种：

- **对角缩放：**将方程组中的每个变量除以其系数矩阵的对角线元素。
- **平衡缩放：**将方程组中的每个变量除以其系数矩阵中所有元素的绝对值之和。

% 对角缩放
A_scaled = diag(diag(A)) \ A;
b_scaled = diag(diag(A)) \ b;

% 平衡缩放
A_scaled = bsxfun(@rdivide, A, sum(abs(A), 2));
b_scaled = bsxfun(@rdivide, b, sum(abs(A), 2));

#### 4.1.2 求解结果后处理

求解器得到的非线性方程组解可能存在误差，需要进行后处理以提高精度。常用的后处理方法包括：

- **结果验证：**将求得的解代入原方程组中，计算残差并验证是否满足精度要求。
- **迭代精化：**使用求得的解作为初始值，继续迭代求解，直到满足精度要求。
- **平滑处理：**对求得的解进行平滑处理，减少噪声和异常值的影响。

% 结果验证
residual = A * x - b;
max_residual = max(abs(residual));

% 迭代精化
x_refined = fsolve(@(x) A * x - b, x);

% 平滑处理
x_smoothed = smoothdata(x, 'gaussian', 5);

### 4.2 并行求解和优化

#### 4.2.1 并行计算原理

并行计算是利用多核处理器或多台计算机同时执行任务，提高计算效率。MATLAB支持两种并行计算模式：

- **共享内存并行：**多个处理器共享同一个内存空间，可以访问相同的变量。
- **分布式内存并行：**每个处理器拥有自己的内存空间，通过消息传递进行通信。

#### 4.2.2 MATLAB并行求解方法

MATLAB提供了多种并行求解方法，包括：

- **并行求解器：**MATLAB内置了并行求解器，如 `parfeval` 和 `spmd`，可以自动将任务分配给多个处理器。
- **并行池：**MATLAB并行池可以创建多个工作进程，并行执行任务。
- **GPU加速：**MATLAB支持使用GPU加速计算，利用GPU强大的并行计算能力。

% 并行求解器
parfeval(@fsolve, 1, A, b);

% 并行池
pool = parpool;
parfor i = 1:100
    x_i = fsolve(@(x) A * x - b, x0);
end

% GPU加速
A_gpu = gpuArray(A);
b_gpu = gpuArray(b);
x_gpu = gpuArray(x0);
x_gpu = fsolve(@(x) gather(A_gpu * x - b_gpu), x_gpu);

# 5.1 求解失败原因和解决方法

在使用MATLAB求解非线性方程组时，可能会遇到求解失败的情况。常见的求解失败原因包括：

### 5.1.1 收敛问题

收敛问题是指求解器无法在给定的最大迭代次数内找到满足收敛条件的解。收敛问题可能由以下原因引起：

- **初始值选择不当：**初始值对求解器的收敛性有很大影响。如果初始值离解太远，求解器可能无法收敛。
- **函数不可导或不连续：**如果被求解的函数不可导或不连续，求解器可能无法找到精确的解。
- **函数存在多个解：**如果被求解的函数存在多个解，求解器可能无法找到所有解，或者找到局部最优解而不是全局最优解。

**解决方法：**

- 尝试使用不同的初始值。
- 检查函数是否可导和连续。
- 尝试使用不同的求解器，例如，如果牛顿法不收敛，可以尝试拟牛顿法或共轭梯度法。

### 5.1.2 精度问题

精度问题是指求解器找到的解与实际解之间的误差过大。精度问题可能由以下原因引起：

- **函数过于复杂：**如果被求解的函数过于复杂，求解器可能无法找到精确的解。
- **求解器精度设置过低：**求解器精度设置会影响求解结果的精度。
- **计算机精度限制：**计算机精度有限，可能会导致求解结果与实际解之间存在微小的误差。

**解决方法：**

- 尝试使用更高精度的求解器。
- 提高求解器精度设置。
- 使用更强大的计算机进行求解。

### 5.1.3 奇异问题

奇异问题是指被求解的函数的雅可比矩阵奇异。奇异问题会导致求解器无法求解线性方程组，从而导致求解失败。

**解决方法：**

- 检查函数的雅可比矩阵是否奇异。
- 如果雅可比矩阵奇异，可以尝试使用正则化技术或奇异值分解（SVD）来解决奇异问题。

# 6. MATLAB非线性方程组求解应用案例**

非线性方程组求解在工程、科学计算等领域有着广泛的应用。本章将展示MATLAB非线性方程组求解器在不同应用场景中的具体案例。

### **6.1 工程问题求解**

**6.1.1 结构力学分析**

在结构力学分析中，需要求解复杂结构的平衡方程。这些方程通常是非线性的，可以通过MATLAB非线性方程组求解器求解。例如，考虑一个简支梁的弯曲问题，其平衡方程为：

syms y(x);
eq = diff(diff(y(x), x), x) + q(x);

其中，`y(x)`为梁的挠度，`q(x)`为分布载荷。可以使用`fsolve`函数求解此方程组：

y0 = 0; % 初始猜测
sol = fsolve(eq, y0);

**6.1.2 流体力学模拟**

在流体力学模拟中，需要求解纳维-斯托克斯方程组。这些方程组是非线性的，可以通过MATLAB非线性方程组求解器求解。例如，考虑一个二维不可压缩流体的流动问题，其纳维-斯托克斯方程组为：

syms u(x, y), v(x, y), p(x, y);
eq1 = diff(u, x) + diff(v, y) == 0;
eq2 = diff(u, y) - diff(v, x) == 0;
eq3 = -diff(p, x) + mu * (diff(diff(u, x), x) + diff(diff(v, y), y)) == 0;
eq4 = -diff(p, y) + mu * (diff(diff(v, x), x) + diff(diff(u, y), y)) == 0;

其中，`u(x, y)`和`v(x, y)`为速度分量，`p(x, y)`为压力，`mu`为流体的粘度。可以使用`optimset`函数设置求解器选项，然后使用`fsolve`函数求解方程组：

options = optimset('Display', 'iter'); % 显示迭代信息
sol = fsolve(@(x) [eq1, eq2, eq3, eq4], [0, 0, 0, 0], options);

### **6.2 科学计算应用**

**6.2.1 图像处理**

在图像处理中，需要求解图像增强或恢复等问题的非线性方程组。例如，考虑一个图像去噪问题，其目标函数为：

syms u(x, y);
f = imread('noisy_image.jpg'); % 读取噪声图像
eq = sum(sum((u(x, y) - f(x, y)).^2)); % 平方差目标函数

其中，`u(x, y)`为去噪后的图像。可以使用`fminunc`函数求解此方程组：

u0 = f; % 初始猜测
sol = fminunc(@(x) eq, u0);

**6.2.2 数据拟合**

在数据拟合中，需要求解非线性模型参数，以使模型拟合给定数据。例如，考虑一个非线性回归问题，其模型为：

syms a, b, c;
data = load('data.mat'); % 加载数据
eq = sum((data.y - (a * data.x.^2 + b * data.x + c)).^2); % 平方差目标函数

其中，`a`、`b`和`c`为模型参数。可以使用`lsqnonlin`函数求解此方程组：

options = optimset('Display', 'iter'); % 显示迭代信息
sol = lsqnonlin(@(x) eq, [0, 0, 0], [], [], options);