构建强预测模型：自变量交互项的深度解析

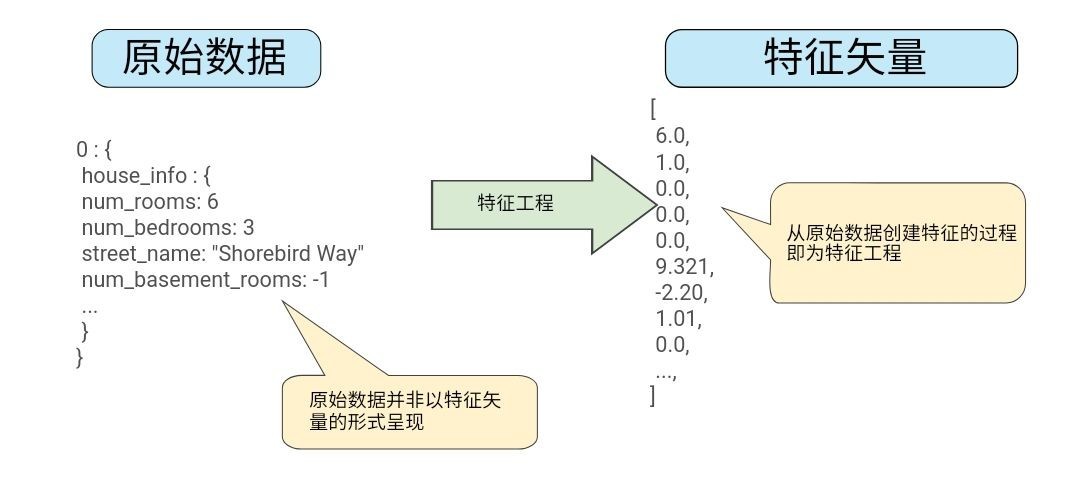
# 1. 预测模型与自变量交互项概述

预测模型是机器学习与统计学中的核心元素，它们通过数学关系对未知结果进行推断。在预测建模中，了解自变量之间的关系至关重要。特别是当这些关系涉及非线性或复杂交互效应时，交互项变得尤为重要。交互项是指两个或多个自变量的组合，它们能够捕捉变量间的相互作用，从而提高模型对数据中复杂模式的预测能力。

本章将概述预测模型中交互项的角色和重要性，通过实例和应用场景，为读者提供一个关于如何在预测模型中有效利用交互项的基础性理解。我们会探讨为什么传统模型可能无法充分捕捉某些数据中的模式，以及如何通过引入交互项来改进这一点。

在后续章节中，我们将深入研究预测模型的理论基础，交互项的数学原理，以及如何在实际应用中识别、选择和利用交互项来构建强大的预测模型。通过这些章节的学习，读者应能够掌握构建和优化含有交互项的预测模型的方法，并能够应对在交互项应用过程中遇到的挑战。

# 2. 理论基础与交互项的数学原理

### 2.1 预测模型的基本概念

在预测模型的开发中，理解其基本概念是至关重要的。预测模型是一类旨在根据历史数据对未来事件或结果进行预测的数学模型。它们被广泛应用于金融分析、市场预测、天气预报以及各类工程问题中。

#### 2.1.1 预测模型的定义与分类

预测模型可以定义为利用现有数据集合，通过统计学、机器学习或其他数学方法，来估计或预测未知或未来值的算法。这些模型根据不同的标准，可以被分类为不同的类型。

一种常见的分类方法是根据模型中变量间的关系是线性的还是非线性的。例如，线性回归模型假设因变量与自变量之间存在线性关系，而非线性模型如决策树、支持向量机和神经网络，可以捕捉数据中的非线性模式。

另外，模型也可以根据其预测的类型，被分为回归模型和分类模型。回归模型预测连续值的输出，而分类模型预测离散的类别标签。

#### 2.1.2 预测模型的性能评估指标

为了衡量模型的预测准确性，我们使用一系列性能评估指标。常见的回归模型性能评估指标包括均方误差（MSE）、均方根误差（RMSE）、均值绝对误差（MAE）和决定系数（R²）。对于分类模型，我们使用准确率、精确率、召回率和F1分数等指标。

为了更深入地理解模型的性能，除了上述指标外，还应该考虑模型的泛化能力，即模型对新未见数据的预测能力。交叉验证是一种常用的评估泛化能力的方法，可以减少过拟合的风险并提供更稳定的性能估计。

### 2.2 自变量交互项的理论基础

在统计学和数据分析中，交互项指的是自变量之间的相互作用，其系数衡量了一个自变量对响应变量的影响如何随着另一个自变量的变化而变化。

#### 2.2.1 交互效应的定义

交互效应通常出现在自变量间存在相互影响时。例如，在教育研究中，性别与教育资源可能共同影响学生成绩，其中性别和教育资源的交互作用就可以作为模型中的一个交互项。

#### 2.2.2 交互项与主效应的关系

一个关键的概念是交互项不应与其构成的主效应混淆。主效应描述的是单个自变量对响应变量的影响，而交互项描述的是两个或多个自变量共同作用时的影响。有时，主效应可能在包含交互项的模型中变得不再显著，因为部分影响被交互项所吸收。

### 2.3 数学模型中的交互项分析

交互项在数学模型中扮演着重要的角色，尤其是在多元线性回归和广义线性模型中，它们能够帮助我们揭示变量间复杂的关系。

#### 2.3.1 多元线性回归中的交互项

在多元线性回归模型中，交互项是通过对两个或多个自变量的乘积来构建的。如果有一个模型，包含了自变量X和Y，那么交互项可以表示为X*Y。这个交互项将被加入到模型中，允许模型捕捉X和Y之间可能存在的非加性关系。

数学上，包含交互项的多元线性回归模型可以表示为：

Y = β₀ + β₁X₁ + β₂X₂ + β₃X₁X₂ + ε

其中`β₃`是交互项的系数，它反映了X₁和X₂的交互效应对Y的影响。

#### 2.3.2 广义线性模型与交互项

广义线性模型（GLM）是多元线性回归模型的扩展，能够适用于更广泛的数据类型，如二项分布、泊松分布等。与多元线性回归类似，GLM也可以通过添加交互项来处理变量间复杂的相互作用。

在GLM中，链接函数允许因变量Y与预测变量之间的关系是非线性的。交互项可以被加入到GLM的预测部分，使得模型能够解释自变量间的交互作用。例如，在泊松分布的GLM中，交互项的使用可以帮助研究者探究风险因素的协同作用对事件发生率的影响。

### 2.4 数学推导和应用实例

为了进一步理解如何在数学模型中加入交互项，我们来看一个简单的应用实例。假设我们有以下简单的线性回归模型：

Y = β₀ + β₁X₁ + β₂X₂ + ε

我们现在想要加入X₁和X₂的交互项，模型将修改为：

Y = β₀ + β₁X₁ + β₂X₂ + β₃X₁X₂ + ε

其中`β₃`是新的交互项系数。通过最小化误差项`ε`的平方和来估计模型参数`β₀`, `β₁`, `β₂`, 和 `β₃`。这可以通过普通最小二乘法（OLS）完成。

一个具体的应用实例：

假设我们正在研究某个地区居民的平均收入(Y)，我们有以下两个预测变量：教育水平(X₁)和工作经验(X₂)。根据研究假设，我们相信教育水平和工作经验之间存在相互作用，并可能对收入产生非加性影响。

首先，我们会收集相关数据并进行数据探索性分析，确定教育水平和工作经验之间是否有显著的交互作用。通过在模型中加入交互项X₁X₂，我们可以使用统计软件来估计该交互项的系数β₃。如果β₃显著不为零，则表明确实存在交互效应，需要在分析中考虑这一点。

数学模型中的交互项是深入理解变量间复杂关系的关键。通过上述理论基础和实例说明，我们可以看到在多元线性回归和广义线性模型中引入交互项的重要性，并且了解如何在实践中操作这些模型。这一理解对于设计出能够准确捕捉数据中隐含模式的预测模型是至关重要的。

# 3. 识别与选择交互项的方法论

## 3.1 数据探索性分析方法

在构建预测模型时，了解数据的基本结构和特征是至关重要的第一步。数据探索性分析方法通过图表和统计量帮助我们直观地认识数据，并识别出可能的交互项。

### 3.1.1 描述性统计与图形分析

描述性统计是理解数据分布特征的一种方法。通过均值、中位数、众数、方差、偏度和峰度等描述性统计量，我们能够快速了解数据的基本属性。图形分析则通过直方图、箱线图、散点图等可视化方法揭示数据中的趋势和模式。

以Python代码为例，我们可以使用`pandas`库和`matplotlib`库进行基本的数据探索：

import pandas as pd
import matplotlib.pyplot as plt

# 加载数据集
data = pd.read_csv("dataset.csv")

# 描述性统计
summary = data.describe()

# 直方图
data['feature_x'].hist()
plt.show()

# 箱线图
data.boxplot(column=['feature_x', 'feature_y'])
plt.show()

# 散点图
data.plot.scatter(x='feature_x', y='feature_y')
plt.show()

### 3.1.2 相关性分析与初步筛选

相关性分析是探索两个或多个变量之间相互关系的统计方法。皮尔逊相关系数是最常见的度量方式，取值范围在-1到1之间，可以反映出变量间是否存在线性关系，以及关系的强度和方向。

例如，我们想要分析`feature_x`和`feature_y`之间的相关性：

correlation_matrix = data[['feature_x', 'feature_y']].corr()
print(correlation_matrix)

我们还可以通过构建散点图矩阵来初步识别多个变量之间的相互关系：

pd.plotting.scatter_matrix(data, figsize=(10, 10), diagonal='kde')
plt.show()

## 3.2 统计检验与模型选择

在