模式分析指南：Lumerical-FDTD原理与应用详解


参考资源链接：[Lumerical-FDTD Solutions中文教程：入门到高级详解](https://wenku.csdn.net/doc/nktii7nkp8?spm=1055.2635.3001.10343)
# 1. Lumerical-FDTD软件概述

## 1.1 软件简介

Lumerical-FDTD是业界著名的时域有限差分（Finite-Difference Time-Domain）方法仿真软件，专注于光子学与电磁仿真。由加拿大Lumerical Solutions公司开发，其精确的计算能力与用户友好的操作界面，使得FDTD仿真在学术界和工业界获得了广泛应用。

## 1.2 应用领域

Lumerical-FDTD软件广泛应用于微纳光学、光波导、光子晶体和非线性光学器件的设计和分析。它帮助工程师和研究人员快速构建物理模型，进行光学性能预测，优化器件设计，并探索新材料和新结构。

## 1.3 软件功能特点

Lumerical-FDTD集成了高级模拟技术，支持复杂几何结构的精确建模，拥有丰富的材料数据库，支持自定义材料参数。软件的操作简单直观，从几何建模到结果后处理，每一环节都充分考虑了用户的需求和易用性。

通过对Lumerical-FDTD软件的简单介绍，我们接下来将深入了解其背后的理论基础和操作细节。

# 2. FDTD理论基础

FDTD（时域有限差分法）是一种用于解决电磁场问题的数值模拟技术，尤其适用于光子学器件的设计和分析。该方法基于时域求解Maxwell方程组，通过离散化处理，将连续的物理场转化为计算机可以处理的离散格式，从而对电磁波在介质中的传播、散射、折射和反射等现象进行模拟。

## 2.1 时域有限差分法的基本原理

### 2.1.1 Maxwell方程的离散化处理

Maxwell方程描述了电磁场与电荷和电流之间的基本关系。在时域有限差分法中，这些方程首先在空间和时间上进行离散化。具体来说，连续的空间被划分为规则的网格，时间被分割为一系列等间隔的步骤。然后，通过差分方法将偏微分方程转化为一组代数方程，这组方程可以用迭代的方式在计算机上求解。

以下是Maxwell方程的离散化示例代码块，展示了如何使用有限差分法对电场和磁场进行迭代更新。

% 假设electric_field和magnetic_field为电场和磁场的矩阵表示
% dt为时间步长，dx, dy, dz为网格空间步长

for t = 1:time_steps
    % 更新电场
    electric_field_new = electric_field + ...
                         dt * ( ... % 计算磁场关于电场的差分项
                               + (magnetic_field(z+1, y, x) - magnetic_field(z, y, x)) / dz
                               - (magnetic_field(z, y+1, x) - magnetic_field(z, y, x)) / dy
                               + (magnetic_field(z, y, x+1) - magnetic_field(z, y, x)) / dx
                               );

    % 更新磁场
    magnetic_field_new = magnetic_field + ...
                         dt * ( ... % 计算电场关于磁场的差分项
                               + (electric_field(z, y+1, x) - electric_field(z, y, x)) / dy
                               - (electric_field(z, y, x+1) - electric_field(z, y, x)) / dx
                               );

    % 应用边界条件和材料特性
    % ...

    % 更新电场和磁场的值为下一时刻的值
    electric_field = electric_field_new;
    magnetic_field = magnetic_field_new;
end

在这段代码中，通过使用有限差分近似来模拟电场和磁场的变化，`electric_field`和`magnetic_field`矩阵在每个时间步骤`t`中更新。这只是一个简化的例子，实际应用中还需要考虑如边界条件、介质材料的参数等因素。

### 2.1.2 数值色散和稳定性条件

数值色散是FDTD模拟中出现的一种现象，指的是模拟的电磁波与实际波的频率之间存在差异。这种色散与模拟中使用的网格尺寸和时间步长直接相关，当数值色散太大时，模拟结果可能与实际情况相差很大。

为了确保模拟的稳定性，必须满足Courant稳定性条件，这个条件规定了时间步长与空间网格尺寸之间的关系。只有当满足这个条件时，模拟才是稳定的，否则会出现数值不稳定现象，导致结果完全不可靠。

c \cdot \Delta t \leq \frac{1}{\sqrt{\frac{1}{(\Delta x)^2} + \frac{1}{(\Delta y)^2} + \frac{1}{(\Delta z)^2}}}

其中`c`是介质中的光速，`Δt`是时间步长，`Δx`、`Δy`、`Δz`是空间网格步长。

## 2.2 FDTD的网格划分与边界条件

### 2.2.1 网格划分技术

FDTD模拟的精确度高度依赖于网格划分的质量。网格越细致，空间中的电磁场变化就越能够被精确捕捉，但这也会导致计算量和内存使用量的增加。通常，网格尺寸应小于问题中最短波长的十分之一，以确保数值色散被限制在可接受范围内。

网格划分不仅与空间分辨率有关，还与材料的特性紧密相关。不同材料的网格尺寸可能会不同，以确保对材料边界的精确处理和对材料属性的正确模拟。

### 2.2.2 边界条件的类型及其影响

在FDTD模拟中，边界条件用于处理电磁波在计算域边界处的行为。常见的边界条件包括吸收边界条件（ABC），周期边界条件（PBC），完美匹配层（PML），以及对称边界条件。不同的边界条件适用于不同的模拟情景。

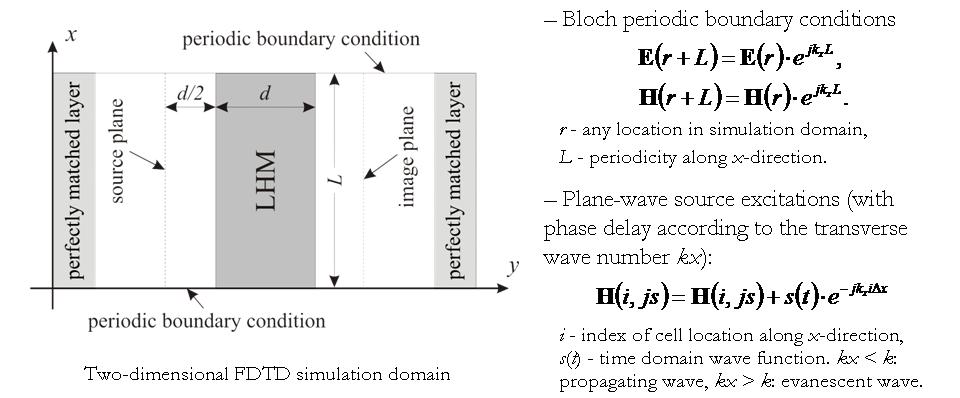
吸收边界条件用于模拟波向外传播时的损耗，防止波在边界处反射。周期边界条件用于模拟周期性结构，使得模拟区域在某个方向上具有无限周期性。完美匹配层是设计用来吸收电磁波的特殊材料层，能有效减少边界反射。这些边界条件对于确保模拟结果的准确性和有效性至关重要。

## 2.3 FDTD中的材料模拟

### 2.3.1 本构关系与材料参数

材料在FDTD模拟中的描述依赖于其电磁特性，即本构关系。这包括材料的介电常数、磁导率以及电导率。在模拟中，这些参数被转化为离散网格上的数值，用于在计算过程中更新电场和磁场。

### 2.3.2 色散材料的数值实现

对于色散材料，其电磁特性与频率有关，这在数值模拟中需要特别处理。FDTD方法采用Debye或Drude色散模型来描述材料的色散特性。在模拟中，需要将色散模型转化为时域的差分格式，以确保模拟结果能够准确反映色散效应。

色散材料参数的数值实现通常涉及到迭代算法，需要在每个时间步长中根据频率相关的色散关系调整材料参数，这样可以在FDTD网格中准确地再现材料的色散行为。

通过深入分析FDTD的基础理论，我们可以为模拟光子学器件及其行为打下坚实的基础。在下一章节中，我们将讨论如何使用Lumerical-FDTD软件进行具体的模拟操作。

# 3. Lumerical-FDTD软件操作

## 3.1 Lumerical-FDTD的用户界面介绍

### 3.1.1 软件布局和主要功能模块

Lumerical-FDTD的用户界面被设计成直观且功能强大，便于用户通过图形化操作进行复杂的光子学模拟。软件布局分为几个主要部分，主要包括：菜单栏、工具栏、状态栏、项目浏览器、布局编辑器、参数设置窗口以及监视器。

- **菜单栏**位于界面顶部，提供各种高级功能，如打开和保存项目、执行模拟、进