散列表深入：解决冲突与哈希函数设计，专家级讲解

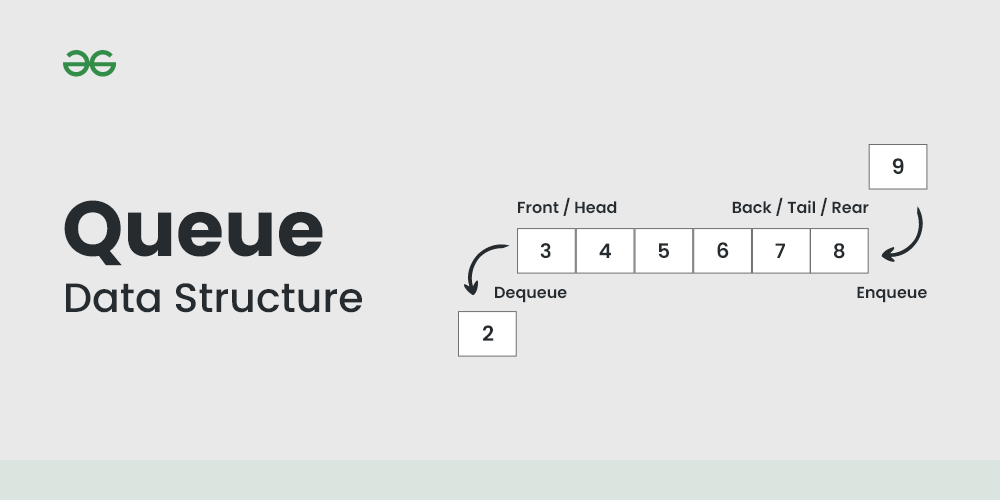
# 1. 散列表的基本概念与应用场景

散列表，也称为哈希表，是一种基于键（Key）的存储数据结构，它通过计算键的哈希值来快速定位键值对（Key-Value Pair）在表中的位置。由于其高效的查找、插入和删除性能，散列表在许多IT领域中有着广泛的应用。

## 1.1 散列表定义与数据模型
散列表的核心思想是利用哈希函数将键映射到数组的索引位置，从而实现快速访问。它的数据模型可以简单地描述为：给定一组键值对，我们希望能够在常数时间内（即O(1)时间复杂度）检索到任意一个键对应的值。

## 1.2 应用场景
散列表的常见应用场景包括：
- 数据缓存：快速检索和更新数据
- 符号表：编程语言中变量的存储和访问
- 数据库索引：加快数据库查询速度
- 唯一性检验：如检测重复项

散列表的数据模型和应用场景之间存在紧密联系，选择合适的散列表结构和哈希函数是优化性能的关键。在后续的章节中，我们将深入探讨散列表的设计原则和性能优化。

# 2. 散列表中冲突的理论基础

### 2.1 冲突的定义与产生原因

#### 2.1.1 什么是散列表冲突

在散列表（哈希表）的设计中，冲突是一个核心问题，它指的是当两个不同的键值（key）在哈希函数的作用下被映射到了同一个哈希地址。由于散列表的存储空间是有限的，当大量的键值被哈希函数映射到相同的位置时，就会出现冲突。冲突的存在会降低散列表的性能，特别是在增加、查找和删除操作时，会导致查找效率和空间利用率的下降。

例如，一个简单的哈希函数是 `h(key) = key mod N`，当两个键值 `key1` 和 `key2` 满足 `key1 mod N = key2 mod N` 时，这两个键值就会冲突，即使 `key1` 和 `key2` 是不同的。

#### 2.1.2 冲突产生的理论分析

理论分析中，我们常常使用“载荷因子”（Load Factor）来描述散列表中冲突的频率。载荷因子定义为散列表中元素的数量（n）与桶（bucket）或槽（slot）的数量（m）的比值，即 `α = n / m`。随着载荷因子的增加，散列表中出现冲突的可能性也随之增加。

从概率论的角度来看，如果哈希函数能够将键值均匀地分布到散列表中，那么任意一个键值冲突的概率应当是 `1/m`。随着散列表中元素数量的增加，冲突的概率也会线性增加，这就是为什么载荷因子对于冲突分析非常重要的原因。

### 2.2 冲突解决策略的比较

#### 2.2.1 开放寻址法

开放寻址法是一种解决冲突的策略，当一个键值通过哈希函数映射到一个已经被占用的位置时，系统会查找另一个空闲位置以存储这个键值。有几种常见的开放寻址策略：线性探测、二次探测和双散列。

- **线性探测**：当发生冲突时，系统会按顺序检查散列表中的下一个位置，直到找到一个空位。
- **二次探测**：系统会以较小的步长（通常是二次幂）进行探测，尝试找到一个空位。
- **双散列**：使用两个哈希函数，当第一个哈希函数发生冲突时，用第二个哈希函数来决定探测的步长。

开放寻址法简单易行，但随着散列表载荷因子的增加，探测的次数也会增多，从而导致性能下降。

#### 2.2.2 链地址法

链地址法通过为散列表的每个槽位维护一个链表来解决冲突问题。当两个键值冲突到同一个槽位时，只需要将它们添加到该槽位的链表中。

- **优点**：链地址法在元素数量增加时能够保持较好的性能，特别是在散列表的大小和元素数量比值较大时。
- **缺点**：需要额外的空间来存储链表指针，以及在查找时需要遍历链表，这可能会导致额外的开销。

链地址法在实现和性能方面通常优于开放寻址法，尤其是在元素数量变化较大时。

#### 2.2.3 比较与选择

选择合适的冲突解决策略依赖于散列表的使用场景和性能需求。例如：

- **内存使用限制**：如果内存使用是一个关键因素，可能会倾向于使用开放寻址法，因为它不使用额外的数据结构。
- **预期的载荷因子**：如果预计载荷因子较高，链地址法可能是更好的选择。
- **插入、删除操作频率**：链地址法在删除操作中更有优势，因为它不需要重新哈希被删除元素之前的元素。

### 2.3 理论与实践的结合

#### 2.3.1 冲突处理方法的适用场景

选择冲突解决策略时，需要考虑散列表的应用需求和性能指标：

- **读多写少的应用**：可以倾向于使用开放寻址法，因为这样的应用对查找时间更为敏感。
- **写多读少的应用**：链地址法通常更有优势，因为它在插入和删除操作上的开销较小。
- **元素分布不均匀**：在某些应用中，如果预先知道键值的分布非常不均匀，可能需要自定义哈希函数或选择更为复杂的冲突解决策略。

#### 2.3.2 理论分析对实践的指导意义

理论分析可以指导实践中的决策：

- **性能优化**：通过理论分析可以预测在不同的载荷因子下散列表的性能表现，为性能优化提供依据。
- **成本效益分析**：理论模型可以帮助我们权衡空间与时间成本，决定在特定应用中应该采用哪种冲突解决策略。
- **系统设计**：了解各种冲突解决策略的优缺点能够帮助设计师构建更为稳定和高效的散列表系统。

冲突处理是散列表设计中不可或缺的一部分，理解和恰当的应用冲突解决策略能够显著提升散列表的性能和稳定性。通过实践应用，可以不断优化和调整策略，以适应不断变化的应用需求。

# 3. 哈希函数的设计原则

## 3.1 哈希函数的作用与要求

### 3.1.1 哈希函数的定义和目的
哈希函数是散列表中的核心组成部分，它负责将输入（通常是各种类型的数据）映射到一个整数，称为哈希值，用作散列表的索引。这个索引随后用于快速定位数据在散列表中的存储位置。哈希函数的设计原则至关重要，因为它直接影响到散列表的性能，包括数据的存取速度、内存使用效率，以及最为核心的一个特点——快速的查找能力。

哈希函数的目的在于实现数据的快速检索。在理想情况下，一个好的哈希函数能够保证每个数据项都有唯一的索引，但实际上这几乎是不可能的，因为输入数据的数量通常远大于散列表的大小。因此，哈希函数的设计目标是尽量减少冲突，即确保散列到同一位置的数据项尽可能少。

### 3.1.2 哈希函数的基本要求
一个好的哈希函数应当满足以下基本要求：

1. **快速计算**：哈希函数应当能够迅速地为输入值计算出哈希值。
2. **均匀分布**：哈希值应当均匀分布在整个散列表空间中，避免出现聚集现象。
3. **易于逆向计算**：在安全应用中，除了快速计算外，还需要考虑哈希函数的单向性。
4. **依赖输入数据**：哈希值的计算应当高度依赖于输入数据，即使输入数据有微小变化，