统计推断基础教程


参考资源链接：[统计推断(Statistical Inference) 第二版 练习题 答案](https://wenku.csdn.net/doc/6412b77cbe7fbd1778d4a767?spm=1055.2635.3001.10343)
# 1. 统计推断的概述与重要性

统计推断是数据科学与统计学的核心组成部分，它涉及使用样本数据对整个总体进行推断。通过对样本的分析，我们能够估计总体参数、检验假设以及预测总体的行为。在实际应用中，统计推断为我们提供了一种科学地作出决策的方法论，尤其在面对不确定性时，它能够帮助我们进行有效的推断与预测。

统计推断之所以重要，是因为在大多数情况下，我们不可能观察到整个数据集，而只能通过样本数据来理解总体特征。例如，企业通过市场调查样本预测整体消费趋势，或者医学研究通过临床试验样本评估药物效果。统计推断通过合理的方法，弥补了样本与总体之间的差异，保证了推断的准确性和可靠性。

在接下来的章节中，我们将深入探讨统计推断的理论基础，包括概率论、统计估计理论以及假设检验等。理解这些基本概念与原理对于掌握统计推断技术至关重要，并将为我们在数据分析和科学研究中提供强大的工具。

# 2. 概率论基础

概率论作为统计推断的核心基础，在理解和应用统计方法中占据着不可或缺的地位。本章将从随机变量及其分布开始，深入探讨概率论中的基础概念，为后续的统计估计理论和假设检验原理打下坚实的基础。

## 2.1 随机变量及其分布

随机变量是统计学中的一个基本概念，它是一个能够描述随机事件结果的变量。理解随机变量及其分布是深入统计推断理论的前提。

### 2.1.1 离散型随机变量与概率分布

离散型随机变量是指那些只能取有限个或可数无限个值的随机变量。在现实世界中，离散型随机变量很常见，例如抛硬币时出现正面的次数。

#### 概率质量函数（Probability Mass Function, PMF）

离散型随机变量的概率分布可以通过其概率质量函数来描述。PMF给出了每一个具体取值的概率，满足以下两个条件：

- 对于每一个可能的值 \( x \)，\( P(X=x) \geq 0 \)
- 所有可能值的概率之和为 1，即 \( \sum_{x} P(X=x) = 1 \)

#### 二项分布

二项分布是最常见的离散型概率分布之一。它描述了在固定次数的独立实验中成功次数的概率分布，每个实验的成功概率为 \( p \)。其概率质量函数为：

\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]

其中，\( n \) 是实验次数，\( k \) 是成功的次数，\( \binom{n}{k} \) 是组合数。

### 2.1.2 连续型随机变量的概率密度函数

连续型随机变量可以取任意值，并且这种取值构成了一个区间。例如，测量一个物理量（如物体的重量）时，其结果可以是任何实数值。

#### 概率密度函数（Probability Density Function, PDF）

连续型随机变量的概率通过概率密度函数来描述。虽然单个取值的概率为零，但可以通过计算随机变量落在某个区间内的概率来表达。概率密度函数 \( f(x) \) 的性质如下：

- \( f(x) \geq 0 \) 对于所有的 \( x \)
- 随机变量 \( X \) 落在区间 \( [a, b] \) 内的概率为 \( \int_{a}^{b} f(x)dx \)

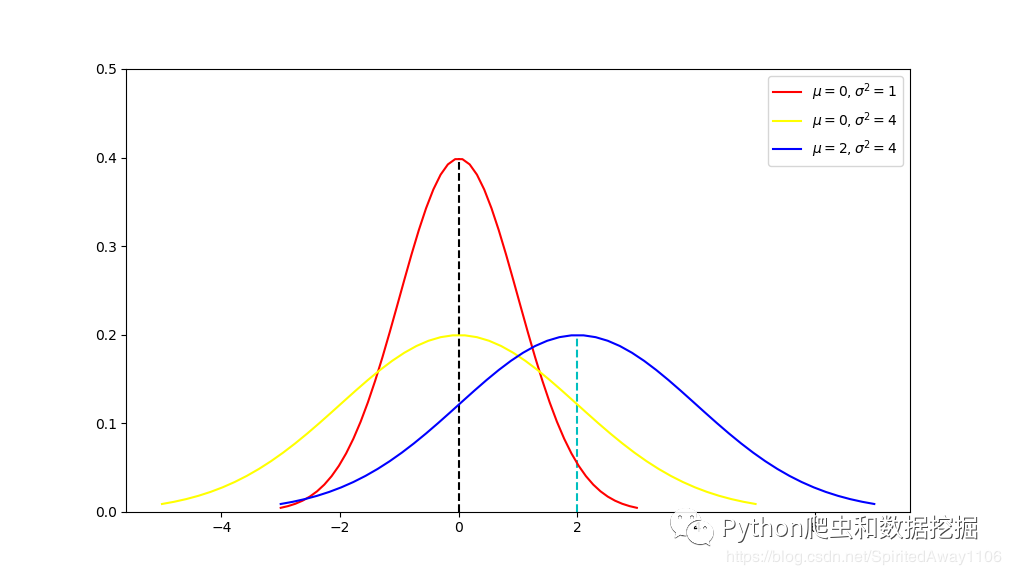
#### 正态分布

正态分布是连续型随机变量中最重要的一种分布，也被称为高斯分布。其概率密度函数为：

\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \]

其中，\( \mu \) 是均值，\( \sigma \) 是标准差。正态分布的图形呈现为一个对称的钟形曲线。

## 2.2 数学期望与方差

数学期望与方差是衡量随机变量特性的重要统计量，它们分别代表了随机变量的集中趋势和离散程度。

### 2.2.1 数学期望的概念和性质

数学期望是随机变量可能取值的加权平均，权数为各取值的概率。对于离散型随机变量，数学期望定义为：

\[ E(X) = \sum_{x} x P(X=x) \]

对于连续型随机变量，数学期望定义为概率密度函数的积分：

\[ E(X) = \int_{-\infty}^{\infty} x f(x)dx \]

数学期望具有以下性质：

- 线性：对于任意常数 \( a \) 和 \( b \)，有 \( E(aX+b) = aE(X) + b \)
- 对于两个随机变量的和，期望等于期望的和：\( E(X+Y) = E(X) + E(Y) \)

### 2.2.2 方差和标准差的意义

方差衡量的是随机变量与其期望值的偏离程度，定义为随机变量的取值与其期望值差的平方的期望值：

\[ Var(X) = E[(X - E(X))^2] \]

方差的性质包括：

- 对于任意常数 \( a \) 和 \( b \)，有 \( Var(aX+b) = a^2 Var(X) \)
- 两个独立随机变量的和的方差等于各自方差的和：\( Var(X+Y) = Var(X) + Var(Y) \)

标准差是方差的正平方根，其具有相同的单位，可以更直观地表达数据的离散程度。

## 2.3 大数定律与中心极限定理

大数定律和中心极限定理是概率论中的两个非常重要的定理，它们为统计推断提供了理论依据。

### 2.3.1 大数定律的表述和应用

大数定律是概率论中描述随机变量序列平均值稳定性的定律。它表明，当独立同分布的随机变量序列足够大时，样本均值以极高的概率接近于它们的期望值。具体地，有两种表述：

- 弱大数定律：对于任意的 \( \epsilon > 0 \)，随着样本数量 \( n \) 的增加，概率 \( P(|\frac{1}{n}\sum_{i=1}^{n}X_i - \mu| < \epsilon) \) 接近 1。
- 强大数定律：随机变量序列的样本均值几乎必然收敛于期望值。

在实际应用中，大数定律支持了抽样调查的可行性。比如在民意调查中，即使抽取的是一个样本，但样本的统计量（如均值或比例）能够在相当程度上代表总体的特征。

### 2.3.2 中心极限定理的证明和含义

中心极限定理描述了大量独立同分布的随机变量之和（或平均值）的分布趋于正态分布的特性。中心极限定理有多种形式，最常用的是林德伯格-列维定理，它在一定条件下断言，对于任意分布的随机变量序列，其样本均值的标准化变量趋近于标准正态分布：

\[ \frac{\sqrt{n}(\bar{X}_n - \mu)}{\sigma} \rightarrow N(0,1) \]

其中，\( \bar{X}_n \) 是样本均值，\( \mu \) 和 \( \sigma \) 分别是总体均值和标准差，\( n \) 是样本量。

中心极限定理的含义非常深远，它意味着在样本量足够大时，总体分布可以不做任何假设，样本均值的分布近似为正态分布，这为许多统计推断方法提供了基础。

在本章节中，我们探讨了概率论中的关键概念，为统计推断提供了坚实的理论基础。随机变量及其分布让我们能够对数据进行分类和分析；数学期望与方差则帮助我们理解数据的特性；而大数定律与中心极限定理则是我们进行统计推断的基石。这些基础概念不仅构成了统计推断的理论框架，也为我们在实践中处理数据提供了方法和工具。在接下来的章节中，我们将进一步讨论统计估计理论和假设检验，它们都是建立在这些基础概率论概念之上的重要统计方法。

# 3. 统计估计理论

## 3.1 点估计

### 3.1.1 估计量的评选标准

在统计推断中，点估计是指用样本数据来估计总体分布的参数。一个好的估计量应该符合几个标准，其中包括无偏性、一致性和有效性。无偏性意味着估计量的期望值等于要估计的总体参数。一致性是指当样本量趋向无穷大时，估计量的值会以概率1收敛于真实的总体参数。有效性是指在所有无偏估计量中，该估计量具有最小的方差，即在相同的样本容量下，它是最精确的。

### 3.1.2 常见的点估计方法

点估计的方法有很多种，最常用的包括矩估计和最大似然估计。矩估计是利用样本矩等于总体矩的性质来求解参数。例如，样本均值可以用来估计总体均值。最大似然估计是基于概率模型，通过最大化似然函数来求解参数，它在理论上具有许多良好的统计性质。

graph TD
A[开始点估计] --> B[选择估计方法]
B --> C[矩估计]
B --> D[最大似然估计]
C --> E[计算样本矩]
D --> F[最大化似然函数]
E --> G[得出参数估计值]
F --> G

在实际应用中，选择哪种点估计方法取决于数据的具体情况和所研究问题的背景。例如，当总体分布形式已知时，最大似然估计往往是首选；如果总体分布未知，矩估计可能更加方便。

## 3.2 区间估计

### 3.2.1 置信区间的定义与计算

区间估计则是给出一个区间，该区间以一定的概率包含总体参数的真实值。这个区间被称为置信区间，它比点估计提供了更多的信息，因为它考虑了估计的不确定性。计算置信区间的一个基本公式是：

\[ \text{置信区间} = \hat{\theta} \pm Z_{\alpha/2} \times SE(\hat{\theta}) \]

其中，\(\hat{\theta}\) 是点估计值，\(Z_{\alpha/2}\) 是标准正态分布表中对应于置信水平的临界值，\(SE(\hat{\theta})\) 是估计的标准误差。

### 3.2.2 母体参数的区间估计实例

假设我们想要估计一个正态总体均值的95%置信区间。首先，我们需要从总体中抽取一个足够大的样本（例如n>30），然后计算样本均值 \(\bar{x}\) 和样本标准差s。接下来，我们使用t分布（因为我们使用了样本标准差）计算标准误差：

\[ SE(\bar{x}) = \frac{s}{\sqrt{n}} \]

假设我们得到的样本均值为100，样本标准差为10，样本大小为64，那么标准误差为：

\[ SE(\bar{x}) = \frac{10}{\sqrt{64}} = 1.25 \]

对于95%的置信水平，我们需要查找t分布表得到自由度为63的t值，假设为2。因此，95%置信区间为：

\[ 100 \pm 2 \times 1.25 = (97.5, 102.5) \]

这表示我们有95%的把握认为总体均值在97.5到102.5之间。

## 3.3 估计量的性质

### 3.3.1 一致性（Consistency）

一致性是衡量估计量好坏的重要性质之一。一个估计量是一致的，如果随着样本量的增加，其估计值收敛到被估计的总体参数。可以通过以下数学表达式来描述一致性：

\[ \hat{\theta}_n \xrightarrow{p} \theta \]

这意味着随着样本容量n趋于无穷大，估计量 \(\hat{\theta}_n\) 以概率1趋近于总体参数 \(\theta\)。一致性是评价估计量是否可靠的关键标准。

### 3.3.2 无偏性（Unbiasedness）

无偏性意味着估计量的期望值等于被估计的总体参数。如果一个估计量是无偏的，那么重复取样多次，估计量的平均值将接近于真实的总体参数值。数学上，无偏性可以表述为：

\[ E(\hat{\theta}) = \theta \]

无偏性确保了长期来看，估计不会系统地偏离真实的参数值。

### 3.3.3 有效性（Efficiency）

有效性是指在所有的无偏估计量中，具有最小方差的估计量。也就是说，对于相同的样本容量，有效性最高的估计量能够提供最精确的估计结果。如果 \(\hat{\theta}_1\) 和 \(\hat{\theta}_2\) 是两个无偏估计量，并且它们的方差分别为 \(Var(\hat{\theta}_1)\) 和 \(Var(\hat{\theta}_2)\)，如果对于所有的 \(\theta\) 都有 \(Var(\hat{\theta}_1) < Var(\hat{\theta}_2)\)，那么我们可以说 \(\hat{\theta}_1\) 比 \(\hat{\theta}_2\) 更有效。

效率通常与Cramér-Rao不等式相关联，它为无偏估计量的方差提供了一个下界。如果一个估计量达到了这个下界，那么它就是有效的。有效性的概念在实际中非常重要，因为它直接影响到统计推断的精确度。

graph LR
A[估计量的性质] --> B[一致性]
A --> C[无偏性]
A --> D[有效性]

B --> E[收敛性]
C --> F[期望值的准确性]
D --> G[方差的最小性]

# 4. 假设检验原理与方法

## 4.1 假设检验的基本概念

### 4.1.1 原假设与备择假设的设定

在统计推断中，假设检验是用来判断样本数据是否支持某个关于总体参数的假设的一种方法。在检验过程中，首先需要明确原假设（Null Hypothesis, H0）和备择假设（Alternative Hypothesis, H1 或 Ha）。原假设通常表述为没有效应、没有差异或没有发现的状态，而备择假设则包含了研究者希望证明的效应或差异。

例如，考虑一个药效测试的案例，原假设可能是“药物A与安慰剂效果无差异”，备择假设则为“药物A比安慰剂效果更好”。在进行假设检验时，研究者需要通过收集数据和计算来支持备择假设或拒绝原假设。

### 4.1.2 错误类型及统计决策

在进行假设检验时，可能会犯两类错误：

1. 第一类错误（Type I Error）：错误地拒绝了一个真实的原假设，其发生的概率通常用α表示，称为显著性水平。例如，将一个有效的药物误认为无效。
2. 第二类错误（Type II Error）：错误地接受了一个假的原假设，其发生的概率用β表示，相应的，(1-β)是检验的功效（Power），即正确拒绝假原假设的概率。

统计决策基于p值和显著性水平α进行。如果计算出的p值小于或等于α，研究者会拒绝原假设，认为有统计学意义的证据支持备择假设；如果p值大于α，则不能拒绝原假设。

## 4.2 常用的检验方法

### 4.2.1 Z检验和T检验

Z检验和T检验是常用的统计假设检验方法。Z检验适用于总体标准差已知的情况，而T检验适用于总体标准差未知且样本量较小时。

#### Z检验的应用

- 适用条件：总体服从正态分布，且总体标准差已知。
- 应用场景：例如，在质量控制过程中，检验产品均值是否符合标准。

flowchart LR
    A[开始] --> B[收集样本数据]
    B --> C[计算样本均值和标准误差]
    C --> D[确定α水平和临界Z值]
    D --> E[计算Z统计量]
    E --> F{Z统计量与临界值比较}
    F -->|Z < -Zα/2 或 Z > Zα/2| G[拒绝原假设]
    F -->|Z在[-Zα/2, Zα/2]之间| H[不能拒绝原假设]
    G --> I[结束]
    H --> I[结束]

#### T检验的应用

- 适用条件：总体服从正态分布，但总体标准差未知。
- 应用场景：例如，小规模样本研究，比较两组学生的考试成绩是否有显著差异。

### 4.2.2 卡方检验和F检验

卡方检验和F检验是用于分类数据和方差比较的假设检验方法。

#### 卡方检验的应用

- 适用条件：适用于频数数据，用于检验两个分类变量是否独立。
- 应用场景：例如，检验疾病的发生是否与特定的生活习惯有关。

flowchart LR
    A[开始] --> B[收集分类数据]
    B --> C[构建列联表]
    C --> D[计算卡方统计量]
    D --> E{比较卡方统计量与临界值}
    E -->|卡方统计量 > 临界值| F[拒绝原假设]
    E -->|卡方统计量 ≤ 临界值| G[不能拒绝原假设]
    F --> H[结束]
    G --> H[结束]

#### F检验的应用

- 适用条件：用于比较两个或多个总体的方差。
- 应用场景：例如，在农作物试验中，检验不同施肥方法对产量方差的影响是否显著。

## 4.3 假设检验的实际应用

### 4.3.1 实验设计与样本数据的收集

假设检验的实际应用首先需要一个严谨的实验设计，包括选择合适的假设检验方法、确定样本大小、收集数据等。样本数据的收集应遵循随机抽样的原则，以保证样本能够代表总体。

### 4.3.2 结果解释和报告撰写

在收集到样本数据后，通过计算相应的统计量和p值，对假设进行检验。如果p值小于显著性水平α，那么拒绝原假设；反之，则不能拒绝原假设。

在撰写报告时，需要清晰地展示实验设计、数据分析的过程、结果和结论。这不仅包括统计表格和图形，还应包括对结果的解释以及可能的限制因素和研究的现实意义。

| 方法    | 检验类型    | 原假设                      | 备择假设                      | 应用场景            |
|---------|-------------|-----------------------------|-----------------------------|---------------------|
| Z检验   | 参数检验    | 总体均值 = 指定值           | 总体均值 ≠ 指定值           | 总体标准差已知      |
| T检验   | 参数检验    | 总体均值 = 指定值           | 总体均值 ≠ 指定值           | 总体标准差未知      |
| 卡方检验| 非参数检验  | 两个分类变量独立            | 两个分类变量相关            | 频数数据比较        |
| F检验   | 方差分析    | 所有总体方差相等            | 至少两个总体方差不同        | 方差比较            |

假设检验是统计推断的关键工具，它不仅要求统计知识的精确运用，还需要对研究设计和数据收集有深入的理解。正确的假设检验应用能够帮助研究者得出可靠结论，并在科研和商业决策中发挥重要作用。

# 5. 统计推断软件应用与案例分析

## 5.1 统计推断软件简介

### 5.1.1 R语言基础

R语言是一个用于统计分析、图形表示和报告的编程语言和软件环境。它在学术界和工业界被广泛使用，特别是适合进行数据挖掘和复杂统计分析的场合。R语言的特点包括丰富的统计函数库、灵活的图形处理能力，以及一个活跃的社区支持。

首先，我们来安装R语言的基础包，打开R语言的控制台，输入以下代码进行安装：

install.packages("stats")

在R语言中，一些基础的统计推断可以直接通过其内置函数完成，比如求解均值、标准差等：

# 生成一个随机样本
sample <- rnorm(100)

# 计算样本的均值
mean_sample <- mean(sample)

# 计算样本的标准差
sd_sample <- sd(sample)

print(mean_sample)
print(sd_sample)

R语言的图形功能非常强大，可以通过ggplot2包来创建高质量的图表：

# 安装ggplot2包
install.packages("ggplot2")

# 导入ggplot2包
library(ggplot2)

# 使用ggplot2画出样本的直方图
ggplot(data.frame(sample), aes(x=sample)) + 
  geom_histogram(bins=30) + 
  labs(title="Histogram of the Sample Data")

### 5.1.2 Python中的SciPy和Pandas应用

Python是一种通用编程语言，它的科学计算库如SciPy和数据处理库如Pandas，使得Python成为处理统计推断任务的流行选择。SciPy库提供了许多用于数学、科学和工程的工具，其中就包括统计模块。Pandas库则提供了快速、灵活和表达能力强的数据结构，专门用于处理结构化（表格、多维、异质）和时间序列数据。

接下来，我们将演示如何在Python中进行一些基本的统计推断：

import numpy as np
import pandas as pd
from scipy import stats

# 生成一个随机样本
sample = np.random.randn(100)

# 计算样本的均值
mean_sample = np.mean(sample)

# 计算样本的标准差
std_sample = np.std(sample)

print(mean_sample)
print(std_sample)

# 使用SciPy进行t检验
t_statistic, p_value = stats.ttest_1samp(sample, 0)
print(f"t-statistic: {t_statistic}, p-value: {p_value}")

Pandas提供了数据框（DataFrame）结构，使得数据处理更加直观：

# 创建一个数据框
df = pd.DataFrame(sample, columns=['Sample'])

# 探索性数据分析：画出直方图
df['Sample'].hist(bins=30)
plt.title("Histogram of the Sample Data")
plt.show()

## 5.2 案例分析与实践

### 5.2.1 实际数据集的探索性数据分析

在这一部分，我们将使用一个真实的数据集来展示探索性数据分析（Exploratory Data Analysis, EDA）的过程。我们将使用Python中的Pandas库来加载数据，然后使用matplotlib和seaborn库进行数据可视化。

首先，我们载入一个经典的数据集，比如泰坦尼克号乘客数据集：

import seaborn as sns
import matplotlib.pyplot as plt

# 加载数据集
titanic = sns.load_dataset('titanic')

# 数据框的前几行数据
print(titanic.head())

# 描述性统计分析
print(titanic.describe())

接下来，我们可以用直方图和箱线图来展示不同变量的分布情况：

# 性别与存活的箱线图
sns.boxplot(x='sex', y='survived', data=titanic)
plt.title('Survival by Sex')
plt.show()

# 年龄的直方图
sns.histplot(titanic['age'].dropna(), kde=True)
plt.title('Age Distribution')
plt.show()

### 5.2.2 完整统计推断流程的演示

在本节中，我们将演示一个完整的统计推断流程。我们将从提出假设开始，进行数据检验，以及最终得出结论。以泰坦尼克号数据集为例，我们想检验一个假设：女性乘客是否比男性乘客有更高的存活率？

我们首先提出零假设（H0）和备择假设（H1）：

- H0: 女性乘客和男性乘客的存活率没有差异。
- H1: 女性乘客的存活率高于男性乘客。

然后，我们使用SciPy的独立样本t检验来检验这个假设：

# 对性别和存活率进行分组统计
survived_by_sex = titanic.groupby('sex')['survived'].value_counts(normalize=True).unstack()

# 进行独立样本t检验
t_statistic, p_value = stats.ttest_ind(titanic[titanic['sex'] == 'female']['survived'],
                                       titanic[titanic['sex'] == 'male']['survived'])

print(survived_by_sex)
print(f"t-statistic: {t_statistic}, p-value: {p_value}")

如果p值小于显著性水平（比如0.05），则我们拒绝零假设，认为有显著的证据表明女性乘客的存活率高于男性乘客。

## 5.3 案例讨论与思考

### 5.3.1 案例讨论中的常见问题

在统计推断的实际应用中，我们经常会遇到一些常见的问题。例如，在上述泰坦尼克号数据集的分析中，我们可能忽略了数据清洗和预处理的步骤，这可能会影响最终的统计推断结果。此外，不同的统计检验方法可能对数据有不同的假设条件，忽略这些条件可能导致错误的结论。

### 5.3.2 统计推断结果的商业及科研应用

统计推断的结果不仅可以帮助我们理解数据，而且在商业和科研领域中具有重要的应用价值。例如，在医药行业，统计推断可以用来评估新药的有效性和安全性；在市场营销领域，可以通过统计推断来评估广告活动的效果；而在科学研究中，统计推断是验证假设，推动知识发展的重要工具。

通过本章的学习，我们不仅掌握了使用统计推断软件进行数据分析的技能，更重要的是学会如何将统计推断应用于实际问题中，从而做出数据驱动的决策。