【Origin高级数据分析】：多项式插值与B样条曲线的应用


参考资源链接：[OriginLab的插值与外推教程——数据处理与科学作图](https://wenku.csdn.net/doc/4iv33a7c5b?spm=1055.2635.3001.10343)
# 1. 多项式插值基础与应用场景

多项式插值是数学和计算机科学中一种非常重要的数学工具，它可以在已知一组离散数据点的情况下，构建出一个多项式函数，来估计未知数据点的值。对于IT行业的专业人士，理解并应用多项式插值在数据处理、图形设计、动画制作等领域有着不可忽视的意义。

## 1.1 多项式插值的基本概念

多项式插值的基本思想是在每个数据点上，多项式函数的值与数据点的值相等。如果我们有一组数据点，我们可以通过求解线性方程组找到唯一的多项式函数，满足在每一个数据点上的插值条件。在实际应用中，我们可以用拉格朗日多项式或牛顿多项式等方法来构造这样的多项式函数。

## 1.2 多项式插值的应用场景

多项式插值广泛应用于物理、工程、金融和计算机图形学等领域。例如，在科学计算中，可以通过插值方法解决微分方程的边值问题；在经济学中，通过插值预测市场数据的趋势；在计算机图形学中，利用插值技术来生成平滑的动画帧序列。在下一章节中，我们将详细分析多项式插值的具体应用实例。

# 2. B样条曲线理论与数学基础

### 2.1 B样条曲线的定义与特性
B样条曲线是计算机图形学中一种重要的参数曲线，它是通过一系列控制点来定义的。B样条曲线的数学定义依赖于B样条基函数，这些基函数是通过递归定义的。B样条曲线不仅能够精确控制形状，还能轻易地处理复杂的几何形状，使之在图形设计和动画制作中得到了广泛应用。

#### B样条曲线的数学表达
B样条曲线的基本数学形式可以表示为：
\[ C(t) = \sum_{i=0}^{n} P_i N_{i,k}(t) \]
其中，\( C(t) \) 表示曲线上点的位置向量，\( P_i \) 是控制点，\( N_{i,k}(t) \) 是B样条基函数，\( n \) 是控制点的数量，\( k \) 是曲线的阶数。

#### B样条曲线的局部性
B样条曲线的一个重要特性是局部控制性。这意味着修改一个控制点只影响曲线的一部分，而不是整个曲线。这对于精细编辑和调整曲线形状特别有用。

### 2.2 B样条曲线的构造方法
B样条曲线的构造包括节点向量的定义、控制点的选择和基函数的计算。通过这些步骤，可以构建出符合设计需求的曲线。

#### 节点向量和基函数
节点向量定义了B样条曲线的参数域。它是一个非递减序列，通常表示为：
\[ U = \{ u_0, u_1, ..., u_{n+k+1} \} \]
其中，\( u_i \) 是节点值，\( n \) 是控制点的数量，\( k \) 是曲线的阶数。

基函数是通过Cox-De Boor递归公式计算得到的，公式如下：
\[ N_{i,0}(t) = \begin{cases}
1 & \text{if } u_i \leq t < u_{i+1} \\
0 & \text{otherwise}
\end{cases} \]

对于 \( k > 0 \)，基函数定义为：
\[ N_{i,k}(t) = \frac{t - u_i}{u_{i+k} - u_i} N_{i,k-1}(t) + \frac{u_{i+k+1} - t}{u_{i+k+1} - u_{i+1}} N_{i+1,k-1}(t) \]

其中，\( i = 0, 1, ..., n \)。

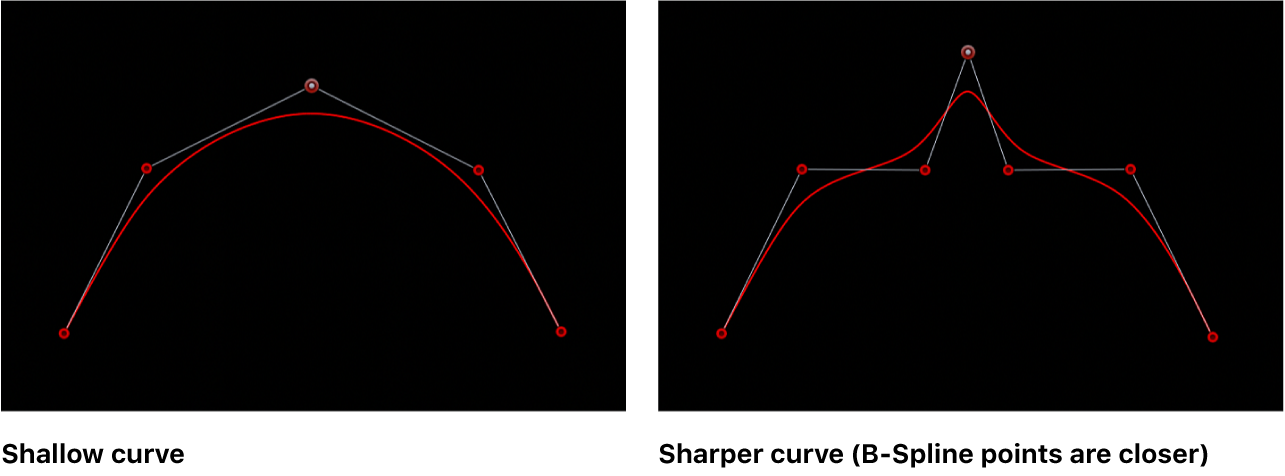
### 2.3 B样条曲线的控制点和曲线形状
B样条曲线的形状直接受控制点的影响。通过改变控制点的位置，可以有效地改变曲线的形状，而不必担心曲线的整体结构。

#### 控制点的作用
控制点可以想象成是拉动曲线的"把手"。当控制点移动时，根据B样条曲线的局部性，曲线会相应地在控制点附近发生弯曲。这种特性使得设计师可以在保持整体形状不变的情况下，对曲线的细节部分进行调整。

#### 曲线的调整策略
在实际应用中，设计师或工程师通常先确定一组大致的控制点，然后通过局部调整这些点来得到所需的曲线形状。当发现曲线有不期望的形状时，可以针对性地微调控制点，而不是重新定义整个曲线。

### 2.4 B样条曲线的编程实现
在计算机上实现B样条曲线的生成，通常需要借助于数值计算库，如Python的SciPy库或C++的Boost库。

#### Python中B样条曲线的实现
以下是一个使用Python和SciPy库来实现B样条曲线的示例代码：

import numpy as np
from scipy.interpolate import BarycentricInterpolator, splev, splrep

# 定义控制点
ctrl_points = np.array([
    [0.0, 0.0], [1.0, 2.0], [2.0, 0.0], [3.0, 1.0], [4.0, 0.0]
])

# 使用spline插值函数来生成B样条曲线
tck, u = splrep(ctrl_points[:, 0], ctrl_points[:, 1], k=3, task=-1, s=0)

# 用于绘制曲线的函数
def绘制曲线(x):
    y = splev(x, tck, der=0)
    return y

# 绘制曲线
x = np.linspace(0, 4, 100)
y = 绘制曲线(x)

# 打印曲线的参数方程
print("B样条曲线参数方程为:")
for i in range(len(x)):
    print(f"C({x[i]:.3f}) = ({x[i]:.3f}, {y[i]:.3f})")

# 注意：由于Python中的绘图通常需要图形界面，这里仅提供了生成和计算曲线参数的代码。

#### 代码逻辑解读
首先，我们定义了一组控制点`ctrl_points`，这些点是曲线形状的基础。接着，我们使用`splrep`函数生成了B样条曲线的参数`tck`和节点向量`u`。这个函数实际上是在计算B样条曲线的基函数的系数。最后，我们使用`splev`函数在给定的参数`x`上计算曲线的值`y`，并打印出曲线的参数方程。

### 2.5 B样条曲线的应用场景分析
B样条曲线广泛应用于各种领域，包括图形设计、动画制作和CAD/CAM等。

#### 图形设计中的应用
在图形设计领域，B样条曲线用于创建平滑的轮廓和复杂的形状。设计者可以通过调整控制点，快速迭代出多种设计选项，最终得到美观且实用的设计方案。

#### 动画制作中的应用
在动画制作中，B样条曲线用于控制动画角色的运动路径。通过精确控制关键帧的控制点，动画师可以制作出流畅且自然的动作序列。

### 2.6 B样条曲线的优势与局限性
B样条曲线因其灵活性和控制性，在许多场合下是一种理想的选择。然而，它也有其局限性，比如在处理高阶曲线时可能出现的计算复杂性。

#### B样条曲线的优势
- 精确控制：通过控制点可以精确地修改曲线形状。
- 局部调整：可以局部修改曲线，而不影响其他部分。
- 平滑性：B样条曲线自然平滑，非常适合于设计和动画制作。

#### B样条曲线的局限性
- 计算复杂度：高阶曲线可能需要大量的计算资源。
- 设计难度：对新手来说，设计复杂的曲线形状可能比较困难。

## 第三章：多项式插值的实践应用

### 3.1 数据点插值实例分析
多项式插值是通过找到一个多项式函数，该函数通过所有给定的数据点。多项式插值在实际中有着广泛的应用，比如在科学实验数据的处理和工程技术领域。

#### 3.1.1 插值算法选择与对比
在多项式插值中，最简单的算法是拉格朗日插值和牛顿插值。对于小数据集，这些方法可能效果不错。然而，对于大数据集，由于计算复杂度较高，通常会考虑使用分段插值或者样条插值。

##### 拉格朗日插值
拉格朗日插值是通过以下公式来实现的：
\[ L(x) = \sum_{j=0}^{n} y_j \prod_{i=0, i \neq j}^{n} \frac{x - x_i}{x_j - x_i} \]
其中，\( (x_i, y_i) \) 是给定的数据点，\( n \) 是数据点的总数。

##### 牛顿插值
牛顿插值使用差分表来构造多项式，公式如下：
\[ P(x) = f[x_0] + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1) + ... \]
其中，\( f[x_0, x_1, ..., x_k] \) 表示k阶差分。

#### 3.1.2 插值误差分析与处理
在使用多项式插值时，误差分析是不可或缺的一步。插