【多用户通信系统优化】：LMS算法应用与效率提升


# 摘要
本文全面探讨了多用户通信系统中LMS算法的优化策略及其应用实践。首先，介绍了LMS算法的理论基础，包括自适应滤波器的概念、LMS算法的工作原理以及其数学模型和性能分析。接着，深入分析了LMS算法的优化策略，如算法参数调整、并行化与分布式计算，并通过实例展示了优化后的系统性能提升。此外，本文还探讨了LMS算法在多用户通信系统中的实际应用，如信号处理和系统效率提升。最后，对未来LMS算法的发展趋势和可能的技术革新进行了展望，特别强调了机器学习、大数据和云计算技术对通信系统优化的影响。本文旨在为通信系统设计者提供深入的技术洞察，并指出优化方向，以应对多用户环境中的挑战。

# 关键字
多用户通信系统；LMS算法；自适应滤波器；并行化计算；系统性能优化；信号处理

参考资源链接：[LMS算法详解：推导、应用与MATLAB实践](https://wenku.csdn.net/doc/40pm4tthai?spm=1055.2635.3001.10343)
# 1. 多用户通信系统优化概述

在现代通信网络中，如何在有限的频谱资源中高效地处理来自多用户的信号是一个重大挑战。本章将简要介绍多用户通信系统优化的核心概念、优化的目标以及优化策略的重要性。

## 1.1 通信系统的优化目标

通信系统的优化目标通常涉及提高信号的传输质量、增强系统容量和扩展频谱效率。这些目标需要通过减少干扰、改善信号检测技术以及提升信号处理算法的性能来实现。

## 1.2 优化技术的发展简史

从早期的频分多址(FDMA)到后来的时分多址(TDMA)和码分多址(CDMA)，多用户通信系统的技术一直在不断演进。随着算法的更新换代，特别是自适应滤波技术的引入，进一步推动了系统的优化与性能提升。

## 1.3 优化策略的多维度考量

系统优化不是单一维度的问题，它涉及到频谱资源管理、信号处理、网络协议、服务质量(QoS)保障等多个方面。优化策略需要从这些多维因素出发，结合最新的技术和算法来设计和实施。接下来的章节将深入探讨LMS算法及其在多用户通信系统优化中的应用。

# 2. ```
# 第二章：LMS算法理论基础

## 2.1 自适应滤波器与LMS算法原理
### 2.1.1 自适应滤波器的概念和作用
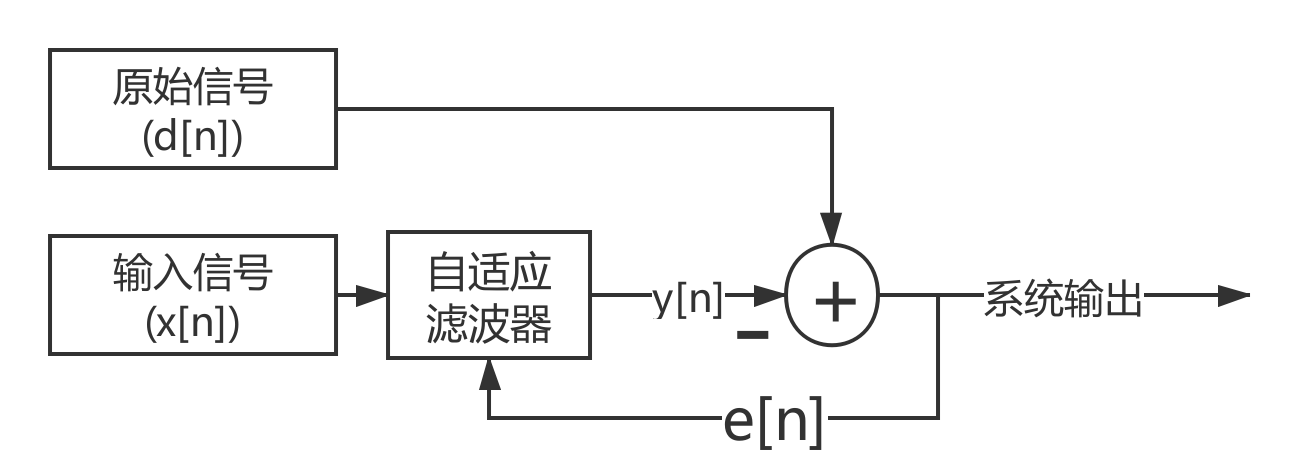
自适应滤波器是一种能够根据输入信号动态调整其参数的滤波器。与传统的固定系数滤波器不同，自适应滤波器可以实时跟踪输入信号的统计特性，并通过自身的算法更新来优化其性能。在许多信号处理的应用中，如回声消除、噪声抑制和线性预测编码等，自适应滤波器能有效适应环境变化，提供理想的滤波效果。

自适应滤波器的主要作用在于其能够自动适应环境变化，并快速收敛到最优解。其核心功能包括：
1. **信号预测**：对未来的信号值进行预测。
2. **系统识别**：估计一个系统的特性，如估计信道特性。
3. **信号分离**：从混合信号中分离出所需信号。
4. **回声消除**：在通信系统中消除回声，改善通话质量。

### 2.1.2 LMS算法的工作原理和特点
LMS（Least Mean Square）算法是一种简单而有效的自适应滤波算法，其核心思想是通过最小化误差信号的平方来更新滤波器的权重。LMS算法的优点在于其简单性、易实现性和稳定性。

LMS算法通过迭代的方式进行滤波器权重的更新。具体步骤如下：
1. 初始化滤波器权重为零或者小的随机数。
2. 采集当前的输入信号向量和期望信号。
3. 使用当前的权重计算滤波器的输出。
4. 计算输出信号与期望信号之间的误差。
5. 根据误差信号和输入信号调整滤波器权重。
6. 返回步骤2，重复迭代直到收敛。

LMS算法的特点包括：
- **算法简单**：计算复杂度低，易于硬件实现。
- **稳定性**：保证了算法的稳定性。
- **易理解**：数学推导相对容易，适用于教学和工程实践。

### 2.2 LMS算法的数学模型和性能分析
#### 2.2.1 数学模型构建
LMS算法的数学模型可以描述为一个优化问题，其目标是最小化滤波器输出与期望信号之间的均方误差（MSE）。具体数学表达式为：

\[ J(n) = E[|d(n) - \mathbf{x}^T(n) \mathbf{w}(n)|^2] \]

其中，\( J(n) \)表示在第\( n \)次迭代时的均方误差，\( d(n) \)是期望信号，\( \mathbf{x}(n) \)是输入信号向量，\( \mathbf{w}(n) \)是第\( n \)次迭代时的滤波器权重向量。

权重更新的迭代公式可以表示为：

\[ \mathbf{w}(n+1) = \mathbf{w}(n) + \mu \mathbf{x}(n) e(n) \]

其中，\( \mu \)是步长因子，\( e(n) \)是第\( n \)次迭代时的误差信号。

#### 2.2.2 算法稳定性和收敛速度分析
算法的稳定性是自适应滤波器设计中非常重要的一个方面。LMS算法的稳定性主要取决于步长因子\( \mu \)的选择。步长因子过大可能导致算法发散，过小则导致收敛速度过慢。因此，合理选择步长因子是实现LMS算法的关键。

收敛速度是指算法权重向最优值收敛的速度。收敛速度与输入信号的自相关矩阵的特征值分布有关。一般而言，输入信号相关矩阵的特征值分布越接近，收敛速度越快。

## 2.3 LMS算法与其他算法的比较
### 2.3.1 与RLS算法的对比
LMS算法与RLS（Recursive Least Squares）算法是两种常用的自适应滤波算法。RLS算法与LMS算法的主要区别在于权重更新的方式不同。

- **收敛速度**：RLS算法具有更快的收敛速度，特别是在信号自相关矩阵特征值分布不均匀时，其性能明显优于LMS算法。
- **计算复杂度**：RLS算法的计算复杂度高于LMS算法，尤其是当信号的维度较大时，RLS算法的计算负担明显加重。
- **稳定性**：RLS算法对于步长参数的选择要求不如LMS算法严格，更容易保证算法的稳定性。

### 2.3.2 与Kalman滤波器的对比
Kalman滤波器是一种基于模型的滤波方法，它利用信号的统计特性进行预测和更新滤波器状态。与LMS和RLS这些基于梯度下降方法的自适应滤波器相比，Kalman滤波器具有以下特点：

- **系统模型依赖**：Kalman滤波器需要一个准确的系统模型和噪声统计信息，而LMS和RLS算法则不需要。
- **滤波精度**：在模型准确的情况下，Kalman滤波器通常能提供比LMS和RLS更高的滤波精度。
- **计算复杂度**：Kalman滤波器的计算复杂度通常高于LMS和RLS算法。

| 滤波算法 | 特点 | 适用场景 |
|---------|------------------------|------------------------------------|
| LMS | 算法简单，低计算复杂度，稳定性好 | 信号特征变化不大，实时处理需求较高 |
| RLS | 收敛速度快，高计算复杂度 | 信号特征变化大，可以接受较高的计算复杂度 |
| Kalman | 模型依赖，高滤波精度 | 拥有准确模型，对滤波精度要求高的场景 |

graph TD
A[LMS算法原理] --> B[自适应滤波器概念]
A --> C[LMS工作原理]
B --> B1[信号预测]
B --> B2[系统识别]
B --> B3[信号分离]
B --> B4[回声消除]
C --> C1[迭代更新权重]
C --> C2[误差最小化]

A --> D[数学模型]
A --> E[性能分析]
D --> D1[均方误差最小化]
D --> D2[权重更新迭代公式]
E --> E1[稳定性分析]
E --> E2[收敛速度分析]

A --> F[算法比较]
F --> G[RLS算法对比]
F --> H[Kalman滤波器对比]
G --> G1[收敛速度和计算复杂度]
G --> G2[稳定性分析]
H --> H1[系统模型依赖和滤波精度]
H --> H2[计算复杂度]

# 以下是一个简单的LMS算法的Python实现代码

class LMSFilter:
def __init__(self, num_taps, step_size):
# 初始化权重和步长因子
self.weights =