【快速排序的极致优化】：应用与技巧，速度提升不是梦

# 1. 快速排序算法概述

快速排序（Quick Sort）算法由C.A.R. Hoare在1960年提出，是一种高效的排序算法。它采用了分治法（Divide and Conquer）的策略，通过一个划分操作将待排序的数组分为两个子数组，其中一个的所有数据都比另一个的要小，然后递归地对这两个子数组继续进行排序，整个排序过程递归进行，直到所有子数组只包含一个元素为止。

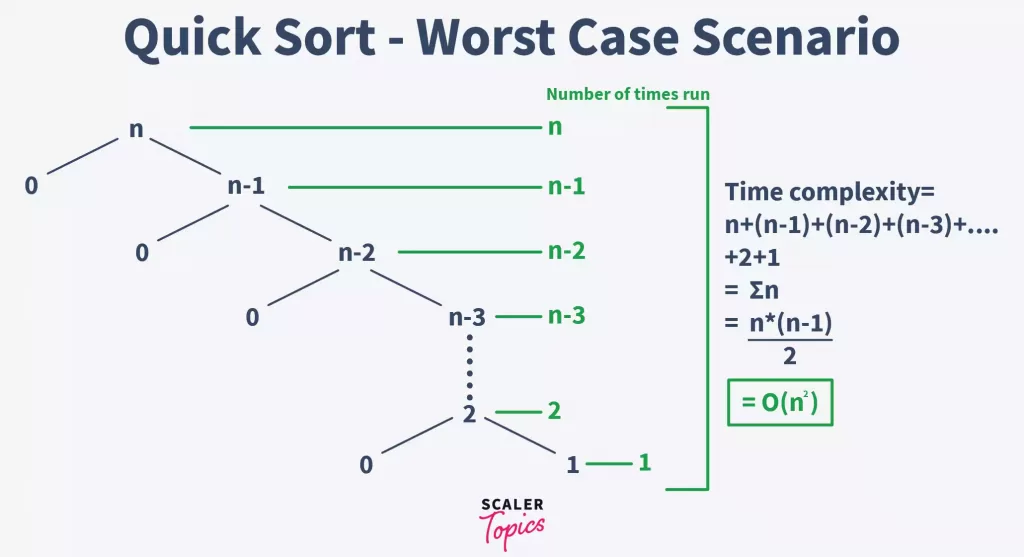
快速排序的核心操作是分区（Partitioning），即将数组分为独立的两部分，其中一部分的所有数据都比另一部分的所有数据要小。快速排序的平均时间复杂度为O(n log n)，但由于分区的原因，最坏情况下可能退化到O(n^2)，这通常发生在每次分区操作选择到的是最小或者最大元素时。

由于其高效的平均性能，快速排序被广泛应用于各种数据处理场景中，尤其是在需要处理大数据集时。它的空间复杂度为O(log n)，因为它通常采用原地排序（In-Place Sorting），不需要额外的存储空间。在本章的后续部分，我们将深入探讨快速排序算法的理论基础，以及它的实现和优化策略。

# 2. 快速排序算法的理论基础

### 2.1 快速排序算法原理

#### 2.1.1 分区过程解析

快速排序的核心在于分区操作，它将数组分为两个部分，其中一部分的所有元素都不大于另一部分的任何元素。这个过程通常称为“划分”（Partitioning）。划分操作一般选择一个元素作为基准（Pivot），重新排列数组，使得左边的元素小于等于基准，右边的元素大于等于基准。

划分过程通常由左右两个指针从数组两端开始，向中间移动。左指针向右移动直到找到大于等于基准的元素，右指针向左移动直到找到小于等于基准的元素，如果两个指针都停下了，则交换它们所指的元素。重复此过程直到左右指针相遇，最后基准元素所在的正确位置就是划分的分界点。

这里提供一个基本的分区操作的伪代码：

function partition(array, low, high) {
    pivot = array[high] // 选择基准元素
    i = low // i指向比基准小的区域的下一个位置
    for j = low to high - 1 do {
        if array[j] <= pivot then
            swap array[i] with array[j]
            i = i + 1
        end if
    end for
    swap array[i] with array[high] // 将基准元素放到正确的位置
    return i // 返回基准元素的位置
}

#### 2.1.2 递归机制详解

快速排序是一种递归算法，它利用了分治策略。一旦基准元素被放置到了正确的位置，算法递归地对基准左右两侧的子数组进行同样的排序操作。这种递归操作可以保证整个数组变得有序。

递归的终止条件是子数组的大小缩小到0或者1，这种情况下子数组已经有序，不需要进一步排序。

下面是一个递归版本快速排序的伪代码：

function quickSort(array, low, high) {
    if low < high then
        p = partition(array, low, high) // 划分数组并获得基准的位置
        quickSort(array, low, p - 1) // 递归排序基准左侧的子数组
        quickSort(array, p + 1, high) // 递归排序基准右侧的子数组
    end if
}

在上述伪代码中，`quickSort` 函数将原数组进行排序，它接受数组以及子数组的起始和结束位置作为参数。每次递归调用都将数组划分成更小的部分，直到满足终止条件。

### 2.2 快速排序的性能分析

#### 2.2.1 时间复杂度与空间复杂度

快速排序的平均时间复杂度为 O(n log n)，在最坏情况下为 O(n^2)。快速排序的平均性能优越，但在极少数情况下，当输入数组已经基本有序或完全有序时，性能会急剧下降。为了避免这种情况，通常需要选择一个好的基准元素，或者采用其他的优化手段。

快速排序的空间复杂度主要取决于递归的深度。最坏情况下的空间复杂度为 O(n)，平均情况下为 O(log n)，这是因为快速排序不需要额外的存储空间，它利用的是原数组空间。快速排序在栈上的使用主要来自于递归调用。

#### 2.2.2 算法稳定性和比较次数

快速排序是一个不稳定的排序算法，因为在排序过程中，元素的相对顺序可能会改变。例如，有多个具有相同值的元素时，它们之间原有的相对位置关系可能会在排序过程中被打破。

比较次数方面，快速排序是基于比较的排序算法。在最好和平均情况下，每次划分都将数组分为两个几乎相等的部分，因此比较次数接近于 O(n log n)。然而，在最坏情况下，每次划分只能将数组分为两个不等的部分，例如，当输入数组已经有序时，比较次数会增加到 O(n^2)。

快速排序的优化方法往往围绕着减少这种最坏情况出现的概率，或是通过其他手段减少比较次数和增加稳定性。这些优化手段包括但不限于随机选择基准、使用插入排序处理小数组、三数取中法等。

在后续章节中，我们将通过实例代码展示快速排序算法的实现，并探讨各种变种和优化策略。

# 3. 快速排序算法的实现

## 3.1 基本快速排序的代码实现

### 3.1.1 递归版本

快速排序的递归版本是该算法最经典且常见的实现方式。它的核心思想是分而治之，通过将数组分为两部分，并递归地对这两部分进行排序，直到达到基本有序的状态。

以下是快速排序递归版本的示例代码：

def quick_sort_recursive(arr, low, high):
    if low < high:
        # Partition the array
        pi = partition(arr, low, high)
        # Sort the two halves
        quick_sort_recursive(arr, low, pi - 1)
        quick_sort_recursive(arr, pi + 1, high)

def partition(arr, low, high):
    # Choose the rightmost element as pivot
    pivot = arr[high]
    i = low - 1
    for j in range(low, high):
        # If current element is smaller than the pivot
        if arr[j] < pivot:
            i += 1
            # Swap elements at i and j
            arr[i], arr[j] = arr[j], arr[i]
    # Swap the pivot element with the element at i+1
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    # Return the partitioning index
    return i + 1

# Example usage:
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quick_sort_recursive(arr, 0, n-1)
print("Sorted array:", arr)

在上述代码中，`quick_sort_recursive` 函数是递归排序的核心，它接受数组和两个索引作为参数，分别表示当前需要排序的数组段的起始和结束位置。`partition` 函数负责找到分区点，并将小于基准值的元素移动到基准的左侧，将大于基准值的元素移动到基准的右侧。这个过程不断地重复，直到数组被完全排序。

### 3.1.2 非递归版本

非递归版本的快速排序利用栈来模拟递归过程。这种实现方式尤其在语言不支持或限制递归深度时特别有用。

下面是非递归版本快速排序的示例代码：

def quick_sort_non_recursive(arr):
    # Create a stack and push initial range onto it
    stack = []
    stack.append((0, len(arr) - 1))

    # Keep popping from stack while it's not empty
    while stack:
        low, high = stack.pop()
        # Partition the array and get the pivot index
        pi = partition(arr, low, high)
        # If there are elements on the left side of the pivot, push left range to