【归并排序的奥秘】：顺序表排序中的高效算法原理

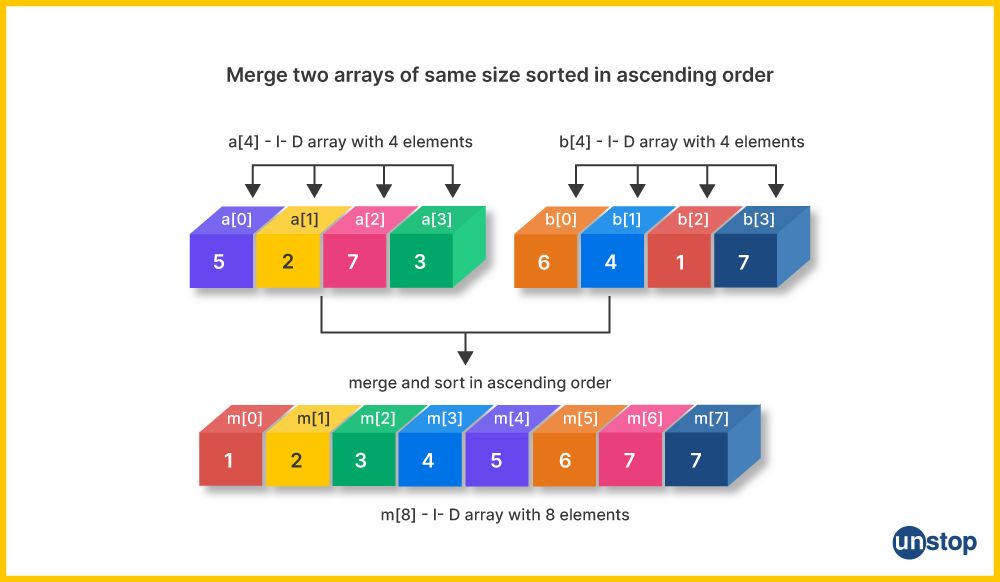
# 1. 归并排序算法概述

## 1.1 算法简介
归并排序是一种经典的排序算法，由约翰·冯·诺伊曼在1945年提出。它的基本思想是“分而治之”，通过将大问题分解成小问题来解决。具体而言，归并排序将数组分成两半，对每一半递归地应用归并排序，最后将排序好的两半合并成一个有序数组。

## 1.2 算法特点
归并排序的主要特点在于其稳定性与时间复杂度。与快速排序等其他排序算法相比，归并排序是稳定的，即它不会改变相同元素之间的相对顺序。然而，它需要额外的内存空间来存储临时数组，这是以空间复杂度为代价换取的时间效率。

## 1.3 算法适用性
尽管归并排序在最坏情况下的时间复杂度为O(n log n)，与快速排序相同，但由于其稳定的性质，它在处理包含大量重复数据的数组时尤其有效。这一点在实际编程中尤为重要，特别是在需要保持元素相对位置的场景，如数据库的排序查询。

归并排序的核心步骤包括拆分和合并，下一章我们将深入探讨其理论基础和具体的算法流程。

# 2. ```
# 第二章：归并排序的理论基础

## 2.1 分而治之的基本思想

### 2.1.1 分而治之的定义与原理

分而治之是一种解决问题的基本方法论，其核心在于将一个复杂的问题分解成多个较小的、易于处理的问题，解决这些小问题，最后再将小问题的解合并起来以形成原问题的解。这个思想不仅适用于排序算法，还广泛应用于算法设计和计算机科学的其他领域。

在排序的上下文中，分而治之原则被应用于将原始数组分成更小的数组，直到每个小数组只包含一个元素或为空。这些小数组很容易排序，因为单个元素或空数组默认是有序的。然后，通过合并有序小数组，逐步构建出更大的有序数组，直至整个数组有序。

### 2.1.2 分而治之算法的典型应用

分而治之策略在很多经典算法中都能见到其身影，比如快速排序、归并排序、二分搜索等。在快速排序中，分治表现在选择一个“轴”元素，然后把数组分成两部分，一部分包含所有小于轴元素的值，另一部分包含所有大于轴元素的值。在二分搜索中，每一步都将搜索区间减半，直到找到目标值或区间为空。

## 2.2 排序算法的分类与比较

### 2.2.1 排序算法的分类

排序算法根据其在处理数据时的不同特点，可以分为几类：比较排序和非比较排序。比较排序算法使用比较来确定元素的顺序，例如冒泡排序、插入排序、选择排序、归并排序、快速排序等。非比较排序算法则不直接通过比较元素来确定顺序，如计数排序、桶排序和基数排序。

### 2.2.2 各种排序算法的时间复杂度对比

对于比较排序算法，其时间复杂度不能低于O(n log n)。归并排序和快速排序恰好都达到了这个下限。非比较排序算法由于有额外的假设和要求，可以在O(n)时间内完成排序，但并非所有情况下都适用。

以下是一些常见排序算法的时间复杂度对比表格：

| 排序算法 | 最佳时间复杂度 | 平均时间复杂度 | 最差时间复杂度 | 空间复杂度 |
|---------|--------------|--------------|--------------|----------|
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) |
| 快速排序 | O(n log n) | O(n log n) | O(n^2) | O(log n) |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(k) |

## 2.3 归并排序的算法流程

### 2.3.1 归并排序的工作原理

归并排序的工作原理基于分而治之。具体来说，归并排序将数组分成两部分，递归地对这两部分应用归并排序，直到每个部分只有一个元素或为空，最后将排序好的部分合并起来。

### 2.3.2 归并排序的主要步骤解析

1. **分割**：将数组分割成两半，直到每个子数组只有一个元素或为空。
2. **排序**：对每个子数组递归调用归并排序。
3. **合并**：将两个有序子数组合并成一个有序数组。

以下是归并排序的主要步骤的伪代码展示：

function mergeSort(array)
    if length(array) <= 1
        return array
    mid = length(array) / 2
    left = array[0..mid]
    right = array[mid..end]

    left = mergeSort(left)
    right = mergeSort(right)

    return merge(left, right)
end function

function merge(left, right)
    result = []
    while length(left) > 0 and length(right) > 0
        if left[0] <= right[0]
            append left[0] to result
            left = left[1..end]
        else
            append right[0] to result
            right = right[1..end]
    end while

    append remaining elements in left or right to result
    return result
end function

以上伪代码中，`mergeSort` 函数是实现归并排序的核心，它不断地将数组分割为更小的部分，并递归排序这些部分。`merge` 函数则是将两个有序数组合并为一个有序数组。通过逐步合并，最终整个数组将被排序。

# 3. 归并排序的实现与优化

归并排序作为一种有效的排序算法，不仅在理论上具有其独特的魅力，而且在实际实现中也展示了其强大的性能。在这一章节中，我们将深入探讨归并排序的实现方法，并探索如何优化它的性能。

## 3.1 归并排序的递归实现

递归实现是归并排序最经典的实现方式，它充分展示了分而治之策略的精髓。我们将从递归的基础概念讲起，然后逐步剖析递归实现归并排序的代码细节。

### 3.1.1 递归的基本概念

递归是一种编程技术，它允许函数直接或间接地调用自身。递归函数通常包含两个主要部分：基本情况和递归步骤。基本情况是递归结束的条件，通常是最简单的情况；递归步骤则是将问题分解为更小的子问题，并对这些子问题进行递归处理。

在归并排序中，递归的基本思想是将数组分成两个子数组，分别对它们进行排序，然后将两个有序的子数组合并成一个有序的数组。这个过程一直递归下去，直到每个子数组只有一个元素，即基本情况。

### 3.1.2 递归实现归并排序的代码剖析

下面是一个使用Python语言编写的归并排序递归实现的示例代码：

def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2 # 找到中间位置，进行分割
left_half = arr[:mid] # 分割出左半部分
right_half = arr[mid:] # 分割出右半部分

merge_sort(left_half) # 对左半部分递归排序
merge_sort(right_half) # 对右半部分递归排序

# 合并两个有序数组
i = j = k = 0
while i < len(left_half) and j < len(right_h