DFT在通信工程中的应用：信号调制与解调的秘密武器

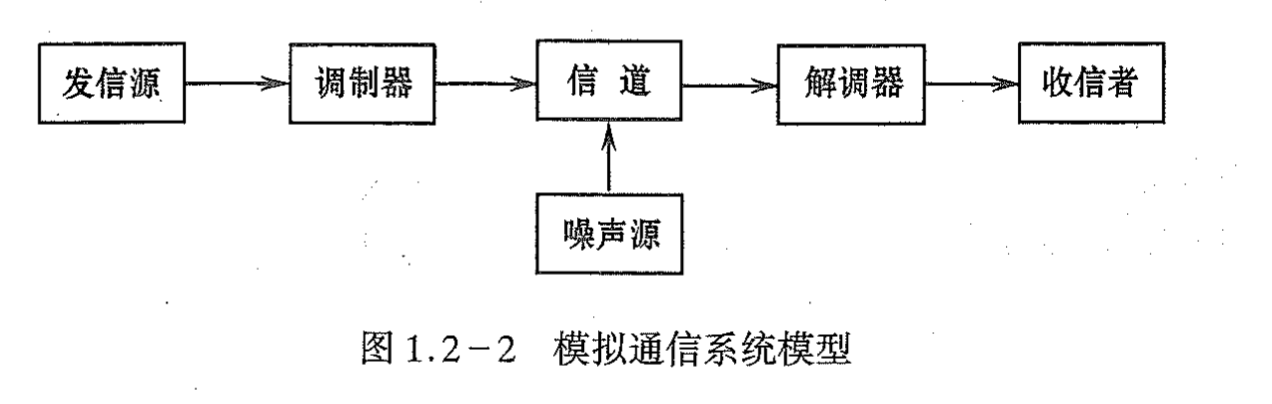
# 1. DFT基础理论

DFT（离散傅里叶变换）是一种将时域信号转换为频域信号的数学变换。它在信号处理和通信工程中有着广泛的应用。

DFT的基本原理是将一个时域信号分解为一系列复指数函数的加权和。这些复指数函数的频率和幅度对应于时域信号的频谱。

DFT的数学表达式为：

X(k) = ∑[n=0:N-1] x(n) * e^(-j * 2 * π * k * n / N)

其中：

* X(k) 是频域信号
* x(n) 是时域信号
* N 是信号长度
* k 是频率索引

# 2. DFT在信号调制中的应用

### 2.1 DFT在调幅调制中的应用

#### 2.1.1 AM调制的原理

调幅调制（AM）是一种将模拟信号（如音频或视频信号）转换为可通过无线电波传输的信号的技术。AM调制的工作原理是改变载波信号的幅度，使其与调制信号成正比。

#### 2.1.2 DFT在AM调制中的作用

DFT在AM调制中发挥着至关重要的作用，它可以将调制信号分解为一系列正弦和余弦分量。这些分量对应于载波信号的频率和幅度变化。通过对这些分量的分析，可以恢复原始的调制信号。

**代码示例：**

import numpy as np
from scipy.fftpack import fft

# 载波信号频率
fc = 1000

# 调制信号频率
fm = 100

# 采样频率
fs = 10000

# 生成载波信号
carrier = np.cos(2 * np.pi * fc * np.arange(0, 1, 1 / fs))

# 生成调制信号
modulating_signal = np.cos(2 * np.pi * fm * np.arange(0, 1, 1 / fs))

# 调制载波信号
modulated_signal = carrier * modulating_signal

# 计算DFT
dft = fft(modulated_signal)

# 提取幅度谱
amplitude_spectrum = np.abs(dft)

**逻辑分析：**

* `fft()`函数对调制信号进行DFT变换，得到复数频谱。
* `np.abs()`函数提取频谱的幅度，得到幅度谱。
* 幅度谱中包含了载波信号和调制信号的频率分量。

### 2.2 DFT在调频调制中的应用

#### 2.2.1 FM调制的原理

调频调制（FM）是一种将模拟信号转换为可通过无线电波传输的信号的技术。FM调制的工作原理是改变载波信号的频率，使其与调制信号成正比。

#### 2.2.2 DFT在FM调制中的作用

DFT在FM调制中同样发挥着重要作用。它可以将调制信号分解为一系列正弦和余弦分量。这些分量对应于载波信号的频率变化。通过对这些分量的分析，可以恢复原始的调制信号。

**代码示例：**

import numpy as np
from scipy.fftpack import fft

# 载波信号频率
fc = 1000

# 调制信号频率
fm = 100

# 采样频率
fs = 10000

# 生成载波信号
carrier = np.cos(2 * np.pi * fc * np.arange(0, 1, 1 / fs))

# 生成调制信号
modulating_signal = np.cos(2 * np.pi * fm * np.arange(0, 1, 1 / fs))

# 调制载波信号
modulated_signal = carrier + modulating_signal * np.cos(2 * np.pi * fc * np.aran