【线性变换的几何奥秘】：二维三维空间变换案例大公开


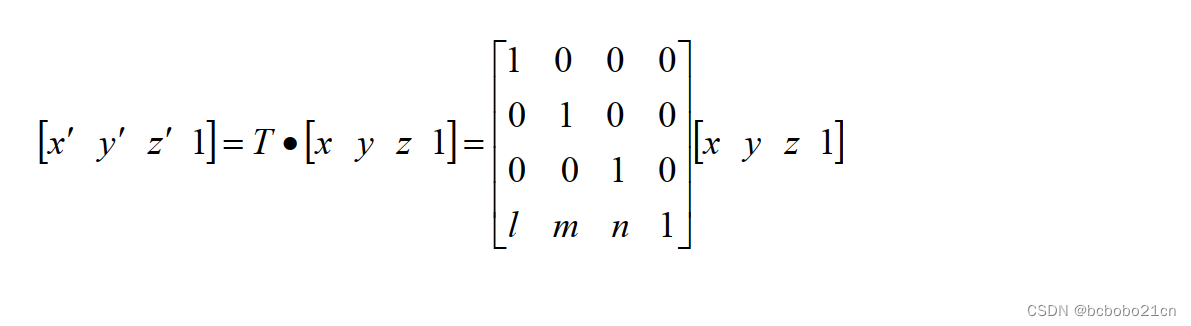
参考资源链接：[陈启宗手写线性系统理论与设计1-9章完整答案揭秘](https://wenku.csdn.net/doc/660rhf8hzj?spm=1055.2635.3001.10343)
# 1. 线性变换的概念与原理

## 1.1 线性变换的定义

线性变换是在向量空间内定义的一种函数，它将一个向量映射到另一个向量，同时满足加法和标量乘法的性质。形式上，如果对于所有的向量 **u** 和 **v** 以及标量 **c**，线性变换 **T** 满足以下两个条件：

- 加法性：**T(u + v) = T(u) + T(v)**
- 齐次性：**T(cu) = cT(u)**

这些性质确保线性变换保持了向量空间的线性结构，是研究变换的重要基础。

## 1.2 线性变换的矩阵表示

线性变换可以通过矩阵与向量的乘法来表示。一个线性变换 **T** 可以用一个矩阵 **A** 来表示，向量 **u** 在变换后的结果 **v** 可以通过矩阵乘法 **v = Au** 来计算。这里的矩阵 **A** 称为变换矩阵。矩阵的每一列对应于基向量在变换后的新位置。

## 1.3 线性变换的几何意义

几何上，线性变换能够改变图形的形状和位置，但保持图形的线性和平行性。例如，旋转变换保持了图形的角度，缩放变换则改变了图形的大小。理解这些几何意义有助于我们直观地把握变换带来的影响，并为进一步分析二维和三维空间中的线性变换打下基础。

# 2. 二维空间中的线性变换

## 2.1 基础变换与矩阵表示

### 2.1.1 平移变换

平移变换是线性变换中最简单的一种，它涉及将图形沿指定方向移动固定距离的操作。在二维空间中，平移变换可以通过一个变换矩阵来表示，该矩阵不改变图形的方向或大小，只改变其位置。

考虑一个向量 \((x, y)\) 在二维空间中的平移，我们可以通过添加平移向量 \((t_x, t_y)\) 来完成。这可以表示为：

\[
\begin{bmatrix}
x' \\
y'
\end{bmatrix}
=
\begin{bmatrix}
x \\
y
\end{bmatrix}
+
\begin{bmatrix}
t_x \\
t_y
\end{bmatrix}
\]

在矩阵表示中，尽管平移操作不是线性变换的一部分，我们仍然可以使用仿射变换矩阵来包含平移，仿射变换矩阵的一般形式是：

\[
\begin{bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{bmatrix}
\]

通过这个矩阵，我们可以将向量 \((x, y, 1)\) 转换为新的位置 \((x', y', 1)\)，其中：

- \(x' = x + t_x\)
- \(y' = y + t_y\)

### 2.1.2 旋转变换

旋转变换是围绕一个点（通常是坐标系的原点或图形的中心）按照指定角度进行旋转。在二维空间中，围绕原点旋转θ角度的旋转矩阵可以表示为：

\[
R(\theta) =
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta)
\end{bmatrix}
\]

我们可以使用以下公式来得到旋转后的向量 \((x', y')\)：

\[
\begin{bmatrix}
x' \\
y'
\end{bmatrix}
=
R(\theta)
\begin{bmatrix}
x \\
y
\end{bmatrix}
\]

其中 \((x, y)\) 是原始向量，而 \((x', y')\) 是旋转后的向量。

### 2.1.3 缩放变换

缩放变换是通过缩放因子对图形的大小进行均匀缩放或非均匀缩放。对于二维空间中的图形，均匀缩放矩阵可以表示为：

\[
S(k_x, k_y) =
\begin{bmatrix}
k_x & 0 \\
0 & k_y
\end{bmatrix}
\]

其中 \(k_x\) 和 \(k_y\) 分别代表在 x 轴和 y 轴方向上的缩放因子。如果 \(k_x = k_y\)，则为均匀缩放；否则为非均匀缩放。应用该矩阵后，原始向量 \((x, y)\) 将转换为 \((k_x x, k_y y)\)。

## 2.2 二维线性变换的组合

### 2.2.1 变换的复合

在线性代数中，多个变换的组合通常通过矩阵乘法来表示。当我们有两个变换，比如旋转和缩放，我们可以按照从右到左的顺序乘以它们的矩阵来获得一个组合变换矩阵。如果我们先对一个向量进行缩放，然后进行旋转，则组合变换矩阵 \(T\) 可以表示为：

\[
T = R(\theta) \cdot S(k_x, k_y)
\]

### 2.2.2 矩阵乘法与变换链

当我们需要应用一系列变换时，可以通过矩阵乘法来合并这些变换矩阵。假设我们有一个向量 \((x, y)\) 需要先缩放后旋转，变换后的向量 \((x'', y'')\) 可以表示为：

\[
\begin{bmatrix}
x'' \\
y''
\end{bmatrix}
=
T
\begin{bmatrix}
x \\
y
\end{bmatrix}
\]

其中 \(T\) 是根据变换顺序计算得到的组合变换矩阵。

## 2.3 二维变换的图形演示

### 2.3.1 利用图形软件观察变换效果

使用图形软件可以帮助我们直观地理解二维变换的效果。大多数图形编辑软件如Adobe Photoshop、GIMP等，提供了旋转、缩放和平移等变换工具，可以直接应用到图形对象上。

### 2.3.2 编程实现二维变换动画

对于编程实现二维变换动画，我们可以使用各种图形库，如JavaScript的p5.js、Python的Pygame等。下面是一个使用Python和Pygame库进行旋转变换的简单示例代码：

import pygame
import sys
import math

# 初始化 Pygame
pygame.init()

# 设置屏幕大小
screen = pygame.display.set_mode((640, 480))

# 加载一个图形
image = pygame.image.load("image.png")
image = pygame.transform.scale(image, (100, 100))

# 设置旋转的中心点
center = (image.get_width() // 2, image.get_height() // 2)

# 将角度从度转换为弧度
angle = math.radians(45)

# 应用旋转变换
rotated_image = pygame.transform.rotate(image, angle)

# 游戏主循环
running = True
while running:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    screen.fill((255, 255, 255))
    screen.blit(rotated_image, (320 - rotated_image.get_width() // 2, 240 - rotated_image.get_height() // 2))

    pygame.display.flip()

pygame.quit()
sys.exit()

这段代码首先加载了一个图形，然后创建了一个旋转45度的变换，并将其绘制到屏幕上。这种编程方式可以用于创建任何类型的二维变换动画。

# 3. 三维空间中的线性变换

## 3.1 三维空间变换的基础

在三维空间中，线性变换通过矩阵乘法实现，它包含了平移、旋转、缩放和剪切等多种变换形式。这些变换是三维计算机图形学和工程模拟等领域的基础。

### 3.1.1 三维平移

三维平移是最基础的变换之一，它不会改变图形的形状和大小，只改变图形在空间中的位置。三维平移变换可以通过下面的矩阵表示：

[ 1   0   0   Tx ]
[ 0   1   0   Ty ]
[ 0   0   1   Tz ]
[ 0   0   0   1  ]

其中，Tx, Ty, Tz 分别是沿 x、y、z 轴方向的平移距离。编程实现三维平移时，只需将此矩阵与三维空间中的点进行矩阵乘法操作。

### 3.1.2 三维旋转变换

旋转变换可以改变物体的方向而不改变其形状和大小。对于三维空间中的旋转，我们通常讨论的是绕某一坐标轴的旋转。以绕 z 轴的旋转为例，旋转角度为 θ，其变换矩阵为：

[ cos(θ) -sin(θ)  0  0 ]
[ sin(θ)  cos(θ)  0  0 ]
[    0       0     1  0 ]
[    0       0     0  1 ]

此矩阵可以使得三维空间中的任何点绕 z 轴旋转 θ 角度。如果需要绕 x 或 y 轴旋转，则变换矩阵略有不同。

### 3.1.3 三维缩放与剪切变换

在三维空间中，缩放变换允许沿 x、y、z 轴独立缩放图形。例如，若沿 x 轴缩放 2 倍，沿 y 轴缩放 1.5 倍，沿 z 轴缩放 0.5 倍，则缩放矩阵如下：

[ 2  0  0  0 ]
[ 0 1.5 0  0 ]
[ 0  0 0.5 0 ]
[ 0  0  0  1 ]

剪切变换能够将图形的形状按照特定方向进行倾斜。例如，在 x 轴和 y 轴上的剪切变换矩阵可能为：

[ 1   Sx  0  0 ]
[ Sy  1   0  0 ]
[ 0   0   1  0 ]
[ 0   0   0  1 ]

其中，Sx 和 Sy 是剪切因子，决定了在相应轴方向上图形的倾斜程度。

### 3.1.3.1 示例代码：三维旋转变换的实现

在 Py