控制理论入门：线性时变系统状态方程离散化基础教程与实战演练


# 摘要
本文系统地介绍了控制理论的基础知识，并重点阐述了线性时变系统的概念、状态空间模型以及线性系统方程的基础。通过分析状态方程的连续时间解和离散化过程，探讨了解析解与数值解的求法，以及如何使用现代计算工具进行系统响应分析和稳定性评估。此外，本文还提供了实战演练，指导如何使用编程技术实现离散状态方程，并通过案例研究展示了离散控制系统的实际应用和深入应用的可能性。最后，展望了离散系统研究的未来方向，包括系统理论的新发展和与其他学科的交叉融合。

# 关键字
控制理论；线性时变系统；状态空间模型；系统稳定性；数值模拟；离散化过程

参考资源链接：[线性时变系统状态方程离散化解析](https://wenku.csdn.net/doc/6byb7vgqto?spm=1055.2635.3001.10343)
# 1. 控制理论概述与线性时变系统的概念

控制理论作为一门研究系统在外界干扰下保持或达到某种特定状态的科学，是工程和科学研究中的基础理论之一。它包含众多分支，其中线性时变系统的研究尤为关键，因为它不仅为分析复杂系统提供了理论基础，还为实际应用提供了可行性。本章节将简述控制理论的基本概念，并详细探讨线性时变系统的特点。

## 1.1 控制理论的基本概念

控制理论是研究如何通过反馈机制使得动态系统达到预期目标的一门学科。它关注系统的状态、输入和输出之间的关系，以及如何通过控制输入来影响系统行为。控制理论的核心在于反馈控制，即根据系统当前状态调整控制输入，以达到期望的输出。

## 1.2 线性时变系统的特点

线性时变系统是指系统的行为可以由线性微分方程描述，并且系统参数随时间变化的系统。与线性时不变系统相比，时变系统具有更加广泛的适用性，能够描述更多的物理现象和实际问题。在实际工程应用中，系统参数的时变性可能由外界环境的改变或系统自身的设计所决定。

## 1.3 线性时变系统的研究意义

研究线性时变系统对于理解复杂系统动态行为具有重要意义。通过建立准确的数学模型，我们可以预测系统的未来行为，并设计出有效的控制策略以适应系统的时变特性。这种研究对于航空航天、机器人技术、信号处理等多个领域都具有重要的应用价值。

graph LR
    A[控制理论概述] --> B[反馈机制]
    B --> C[系统状态]
    C --> D[线性时变系统]
    D --> E[系统建模与分析]
    E --> F[应用与控制策略设计]

在本章中，我们将深入了解控制理论的基础知识，并对线性时变系统的特点进行阐述。之后各章节将进一步探讨如何建立和分析线性系统模型，并最终实现对系统行为的预测和控制。

# 2. 状态空间描述与线性系统方程基础

## 2.1 状态空间模型的建立

### 2.1.1 系统状态的定义

在控制系统理论中，状态是指在某一时刻，能够完全描述系统内部动态行为的所有变量的集合。这些变量称为状态变量，它们构成了系统状态的数学表示。状态空间模型是控制系统设计的核心，它将系统的物理行为转化为数学方程，为系统分析和控制提供了框架。

状态向量通常表示为：

x(t) = [x_1(t), x_2(t), ..., x_n(t)]^T

其中，`x_i(t)` 是第 i 个状态变量，`t` 表示时间，`^T` 表示转置操作，整个向量是一个列向量。状态变量的选择取决于系统的动态特性和控制目标。

### 2.1.2 状态空间方程的推导

状态空间模型由一组微分方程表示，包含了状态方程和输出方程。状态方程描述了系统状态随时间的变化规律，而输出方程则表达了系统输出与状态变量之间的关系。对于线性时不变系统，状态空间方程通常可以表示为：

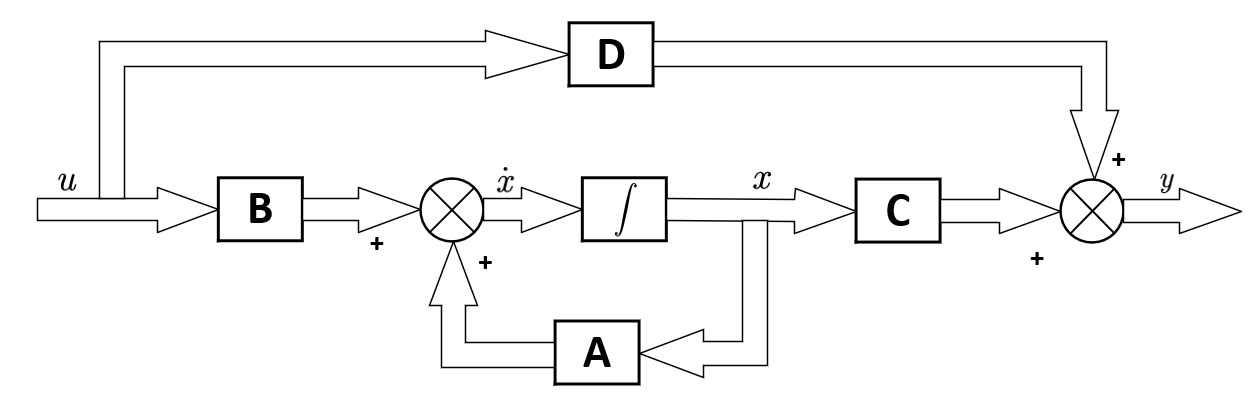
状态方程:  x'(t) = Ax(t) + Bu(t)
输出方程:  y(t) = Cx(t) + Du(t)

在这里，`x'(t)` 表示状态向量的时间导数，`A` 是系统矩阵，`B` 是输入矩阵，`u(t)` 是输入向量，`y(t)` 是输出向量，`C` 是输出矩阵，`D` 是直接传递矩阵。这些矩阵的元素通常是已知的，可以通过物理定律或实验数据获得。

## 2.2 线性时变系统的特性分析

### 2.2.1 系统的动态特性

线性时变系统的动态特性指的是系统对输入信号的响应随时间变化的情况。在状态空间模型中，系统的动态特性主要由系统矩阵 A 决定。对于不同的 A 矩阵，系统可能表现出不同的动态行为，如指数增长、衰减或振荡等。

系统矩阵 A 的特征值对于理解系统动态特性至关重要。如果 A 的所有特征值都具有负实部，那么系统是稳定的。反之，如果至少有一个特征值具有正实部，系统将是不稳定的。

### 2.2.2 系统的可控性和可观性

系统的可控性指的是系统能否通过适当的输入 u(t) 控制其状态 x(t) 在有限时间内达到任意状态。同理，可观性指的是系统状态能否被唯一确定地从系统的输入 u(t) 和输出 y(t) 中观测到。

线性时不变系统的可控性和可观性可以通过卡尔曼分解理论进行分析。如果矩阵 C(A,B) 满足可控性矩阵的秩条件，即 rank(C(A,B)) = n（其中 n 是状态向量的维数），那么系统是可控的。类似地，可观性矩阵 O(A,C) 的秩条件 rank(O(A,C)) = n 表示系统是可观的。

## 2.3 线性系统的数学工具

### 2.3.1 矩阵和线性代数基础

矩阵是线性代数中的核心概念，它是一个以行和列组成的矩形阵列，包含数字、符号或数学表达式。在线性系统的分析中，矩阵用于表示和操作多个变量。

系统矩阵 A、输入矩阵 B、输出矩阵 C 和直接传递矩阵 D 都是矩阵的实例，它们在状态空间模型中扮演着不同的角色。矩阵运算，如矩阵乘法、加法、转置和求逆，是分析和解决线性系统问题的基本工具。

### 2.3.2 线性变换和特征值分析

线性变换是一种特殊的函数，它将向量空间内的一个向量映射到另一个向量，且保持了向量的加法和标量乘法操作。在线性系统中，线性变换通常由矩阵乘法来表示。

系统的特征值是 A 矩阵的特殊值，对应于齐次方程 Ax = λx 的解。求解特征值可以帮助我们了解系统的稳定性和动态行为。特征向量则是与特征值对应的非零向量 x，满足 Ax = λx。

对于特征值 λ 和对应的特征向量 x，我们可以使用以下公式进行求解：

(A - λI)x = 0

其中，`I` 是单位矩阵，`0` 是零向量。只有当 `λ` 使得矩阵 `(A - λI)` 不可逆时，上述方程才会有非零解。

系统矩阵 A 的特征值可以通过求解特征多项式 `det(A - λI) = 0` 来获得。这个多项式的根就是 A 的特征值。

通过特征值和特征向量的分析，我们可以更好地理解系统的动态响应和稳定性。例如，如果所有的特征值都有负实部，则系统是稳定的；如果至少有一个特征值有正实部，则系统是不稳定的。

# 3. 状态方程的连续时间解

## 3.1 解析解的求法

### 3.1.1 拉普拉斯变换方法

在分析连续时间系统的状态方程时，拉普拉斯变换是一种强大的数学工具，它能够将时域中的微分方程转换为s域中的代数方程。这种方法不仅简化了计算过程，还便于分析系统的稳定性和响应特性。

状态方程一般形式如下：

\[
\left\{
\begin{array}{ll}
\dot{x}(t) = Ax(t) + Bu(t) \\
y(t) = Cx(t) + Du(t)
\end{array}
\right.
\]

其中，\(x(t)\)是系统状态向量，\(u(t)\)是输入向量，\(y(t)\)是输出向量，\(A\)、\(B\)、\(C\)和\(D\)分别是状态矩阵、输入矩阵、输出矩阵和直接传递矩阵。

为了求解上述状态方程，应用拉普拉斯变换：

\[
sX(s) - x(0) = AX(s) + BU(s)
\]

其中\(X(s)\)是\(x(t)\)的拉普拉斯变换，\(U(s)\)是\(u(t)\)的拉普拉斯变换。假设初始状态为零，则上式可以简化为：

\[
(sI - A)X(s) = BU(s)
\]

由此，状态向量\(x(t)\)的拉普拉斯变换\(X(s)\)可以表示为：

\[
X(s) = (sI - A)^{-1}BU(s)
\]

现在，我们可以利用拉普拉斯反变换求得状态向量\(x(t)\)的时域解。通过查询拉普拉斯变换表，根据输入\(U(s)\)的表达式进行逆变换，得到\(x(t)\)的具体形式。

### 3.1.2 状态转移矩阵的计算

状态转移矩阵\(\Phi(t)\)描述了系统从初始状态\(x(0)\)到达任意时间\(t\)的状态。它是求解状态方程的关键，因为状态向量的解析解可以通过它来表示：

\[
x(t) = \Phi(t)x(0) + \int_{0}^{t} \Phi(t-\tau)Bu(\tau) d\tau
\]

计算状态转移矩阵\(\Phi(t)\)，首先需要找到矩阵\(A\)的特征值和